
Trong không gian Oxyz, cho hai điểm A(4;-2;1) và B(0;-2;-1). Phương trình mặt cầu có đường kính AB là.
A.x-22+y+22+z2=5
B.x+22+y-22+z2=5
C.x-22+y+22+z2=20
D.x+22+y-22+z2=20
Chọn B
Bạn đang đọc: Trong không gian Oxyz cho 2 điểm A(1;1;1 B(3 1;1 mặt cầu đường kính AB có phương trình là))
Phương pháp:
Phương trình mặt cầu có tâm I(a,b,c) bán kính R là:
Kinh nghiệm khoanh bừa chống điểm liệt
Cách giải:
Tâm mặt cầu là trung điểm của AB, có tọa độ là : I ( – 1 ; 0 ; 1 )
Bán kính mặt cầu :
Câu hỏi:
Trong không gian với hệ tọa độ Oxyz, cho hai điểm \(A(1 ; 2 ; 3) \text { và } \mathrm{B}(-1 ; 4 ; 1)\). Phương trình mặt cầu đường kính AB là:
Lời Giải:
Đây là các bài toán toạ độ Mặt cầu trong phần Hình học OXYZ.
Tâm I của mặt cầu là trung điểm của AB : \ ( I ( 0 ; 3 ; 2 ) \ text {, mặt khác } R ^ { 2 } = I A ^ { 2 } = 1 + 1 + 1 = 3 \ )
Phương trình mặt cầu cần tìm là : \ ( x ^ { 2 } + ( y-3 ) ^ { 2 } + ( z-2 ) ^ { 2 } = 3. \ )
= = = = = = = = = = = = = = =
====================
Thuộc chủ đề: Trắc nghiệm Phương trình mặt cầu và các dạng toán liên quan
Trong khoảng trống Oxyz, cho 2 điểm A ( 1 ; 1 ; 1 ), B ( 1 ; – 1 ; 3 ). Phương trình mặt cầu đường kính AB là
A. ( x – 1 ) 2 + y 2 + ( z – 2 ) 2 = 8
B. ( x – 1 ) 2 + y 2 + ( z – 2 ) 2 = 2
C. ( x + 1 ) 2 + y 2 + z 2 = 13
D. ( x + 1 ) 2 + y 2 + ( z + 2 ) 2 = 8
Trong khoảng trống Oxyz, cho mặt cầu ( S ) : ( x + 1 ) 2 + ( y – 1 ) 2 + ( z + 2 ) 2 = 3 và hai đường thẳng d x : x – 2 1 = y 2 = z – 1 – 1 ; △ : x 1 = y 1 = z – 1 – 1 Phương trình nào dưới đây là phương trình mặt phẳng cắt mặt cầu ( S ) theo giao tuyến là một đường tròn ( C ) có nửa đường kính bằng 1 và song song với d và △.
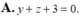
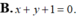
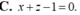
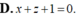
Trong khoảng trống Oxyz, mặt phẳng ( P ) đi qua điểm A ( 1 ; – 1 ; 3 ) song song với hai đường thẳng d : x – 4 1 = y + 2 4 = z – 1 – 2, d ‘ : x – 2 1 = y + 1 – 1 = z – 1 1 có phương trình là :
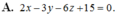
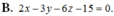
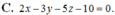
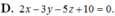
( x – 1 ) 2 + ( y + 2 ) 2 + ( z + 3 ) 2 = 25
A. I(1; -2; -3); R = 25
C. I(-1; 2; 3); R = 25
Trong khoảng trống Oxyz, cho ba mặt cầu lần lượt có phương trình là ( x + 5 ) 2 + ( y – 1 ) 2 + z 2 = 5 ; x 2 + ( y + 2 ) 2 + ( z – 3 ) 2 = 6 và ( x + 1 ) 2 + y 2 + ( z – 4 ) 2 = 9. Gọi M là điểm di động ở ngoài ba mặt cầu và X, Y, Z là những tiếp điểm của những tiếp tuyến vẽ từ M đến ba mặt cầu. Giả sử MX = MY = MZ, khi đó tập hợp những điểm M là đường thẳng có vectơ chỉ phương là
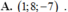
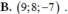
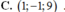
Chống liệt tiếng anh 2021
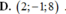
Trong khoảng trống với hệ tọa độ Oxyz, cho mặt cầu ( S ) : ( x + 1 ) 2 + ( y – 1 ) 2 + ( z + 2 ) 2 = 2 và hai đường thẳng d : x – 2 1 = y 2 = z – 1 – 1, ∆ : x 1 = y 1 = z – 1 – 1. Phương trình nào dưới đây là phương trình của một mặt phẳng tiếp xúc với ( S ), song song với d và ∆ ?
A. x+z+1=0
B. x+y+1=0
C. y+z+3=0
D. x+z-1=0
Trong khoảng trống Oxyz, cho tam giác ABC có A ( 2 ; 3 ; 3 ) phương trình đường trung tuyến kẻ từ B là x – 3 – 1 = y – 3 2 = z – 2 – 1, phương trình đường phân giác trong của góc C là x – 2 2 = y – 4 – 1 = z – 2 – 1. Đường thẳng AB có vecto chỉ phương là : A. ( 2 ; 1 ; – 2 )
B. (1;-1;0)
C. (0;1;-1)
D. (1;2;1)
Trong khoảng trống Oxyz, cho mặt cầu ( S ) : ( x – 1 ) 2 + ( y – 1 ) 2 + ( z – 1 ) 2 = 1 và điểm A ( 2 ; 2 ; 2 ). Xét những điểm M thuộc ( S ) sao cho đường thẳng AM luôn tiếp xúc với ( S ). M luôn thuộc một mặt phẳng cố định và thắt chặt có phương trình là
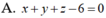
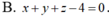
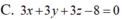
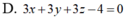
Cho ba điểm A, M, B nằm trên mặt cầu ( S ) thỏa mãn nhu cầu điều kiện kèm theo góc AMB = 90 o. Diện tích tam giác AMB có giá trị lớn nhất là :
B. 2
D. Không tồn tại
Trong khoảng trống Oxyz, cho tam giác ABC với A ( 2 ; 3 ; 3 ) đường trung tuyến kẻ từ đỉnh B là x – 3 – 1 = y – 3 2 = z – 2 – 1 phương trình đường phân giác trong góc C là x – 2 2 = y – 4 – 1 = z – 2 – 1. Đường thẳng AB có một véctơ chỉ phương là :
A. (0;1;-1).
B. (2;1;-1).
C. (1;2;1).
D. (1;-1;0)
Trong hệ tọa độ \ ( Oxyz \ ), cho hai điểm \ ( A \ left ( { 1 ; 2 ; 3 } \ right ), B \ left ( { – 1 ; 4 ; 1 } \ right ) \ ). Phương trình mặt cầu đường kính \ ( AB \ ) là
A.\ ( { \ left ( { x + 1 } \ right ) ^ 2 } + { \ left ( { y – 4 } \ right ) ^ 2 } + { \ left ( { z – 1 } \ right ) ^ 2 } = 12 \ ) B.\ ( { \ left ( { x – 1 } \ right ) ^ 2 } + { \ left ( { y – 2 } \ right ) ^ 2 } + { \ left ( { z – 3 } \ right ) ^ 2 } = 12 \ ) C.\ ( { x ^ 2 } + { \ left ( { y – 3 } \ right ) ^ 2 } + { \ left ( { z – 2 } \ right ) ^ 2 } = 3 \ ) D.
\({x^2} + {\left( {y – 3} \right)^2} + {\left( {z – 2} \right)^2} = 12\)
Video liên quan
Source: http://wp.ftn61.com
Category: Hỏi Đáp
Từ khóa tìm kiếm: phương trình mặt cầu đường kính ab,1 b =,lập phương trình mặt cầu đường kính ab,trong không gian oxyz cho 2 điểm a 1 hai 3 và b 321 phương trình mặt cầu
đường kính ab là,a.1,viết phương trình mặt cầu đường kính ab,b hai,1 b,a:1=,1 + b,1:b,a=1.,a\1,phuong trinh mat cau duong kinh ab,phương trình mặt cầu có đường kính ab,1/1*2+1/2*3,1 a 1 b,b 3 2,1^2-2^2+3^2,trong không gian oxyz cho 2 điểm,x hai y 2 z 2,x^2+y^2+z^2,trong ko gian oxyz,trong không gian,1 hai một ba,1 1 ba,tìm bán kính mặt cầu,trường đại học quốc tế hồng bàng,hình học oxyz,xiaomiviet.
Nội dung khác
Toán học, khoa học tính toán và khoa học về sự sống, 1 b =.
1 cách kha khá có thể xem có ba loại toán có đặc điểm và động lực phát triển khác nhau, lập phương trình mặt cầu đường kính ab.
1 là toán học thuần túy được nghiên cứu với động lực tăng trưởng nội tại của toán học, phuong trinh mat cau duong kinh ab. Toán học
thuần túy phát triển nhanh và sâu theo các chuyên ngành tới mức ví như các nhà toán học kiệt, a\1
xuất David Hilbert và Henri Poincaré ở thế kỷ 19 có thể hiểu sâu được nhiều lĩnh vực toán học
thời ấy, thì ngày nay chừng như không người nào có thể nhìn được bức tranh toàn cục về toán học sâu
sắc như vậy. Hai là toán học đại chúng, gồm những tri thức toán mọi người cần cho cuộc sống
và công tác a=1. hàng ngày. Điều đáng 1:b chú tâm ở đây là giáo dục của ta sẽ đưa thứ toán đại chúng nào
và đưa thế nào tới cho mọi đứa 1 + b ở thời máy tính a:1= và internet này? Ba là toán cho các khoa học
khác, có nội dung và động lực phát triển từ các vấn đề cụ thể của các khoa học này. Chính ở đây,
toán học thể hiện vai trò căn bản b 2 của mình trong khoa học và ảnh hưởng thâm thúy đến sự phát triển
của xã hội.
Toán học, khoa học máy tính viết phương trình mặt cầu đường kính ab và khoa học tính toán
Khoa học máy tính (computer science) hay tin học (informatics) cách đây không lâu được gọi ở ta với tên
công nghệ thông tin (information technology) theo nghĩa rộng của từ này. Khoa học máy tính
được xem là “khoa học về xử lý thông tin tự động bằng máy tính điện tử”. Về bản chất, xử l ý
thông tin là quá trình biến đổi dữ liệu từ dạng này sang dạng khác để thu được thông tin và tri
thức mới.
then chốt của công đoạn “biến đổi dữ liệu” chính là các biến đổi toán học, và do vậy cốt lõi của khoa
học máy tính cũng chính là toán học. 1 Người bạn ở Pháp kể khi là sinh viên tin học, anh đã
sững sờ khi thầy giáo cho xem bức ảnh 1 rừng cây do không quân Mỹ chụp ở Trường Sơn
trong chiến tranh Việt Nam, và qua các phép biến đổi toán học lớp cây xanh đã bị bóc đi để lộ rõ a.1
bên dưới hình các xe tăng của quân nhân miền Bắc. Đây là một thí dụ về chuyển đổi dữ liệu trong xử lý
ảnh.
Trong khoa học máy tính ta luôn gặp các vấn đề toán học, từ bài toán nền tảng NP ≠ P (một trong đường kính ab là”
bảy bài toán do Viện Toán học Clay ban bố vào năm 2000, thử thách các nhà toán học giải
trong thế kỷ 21) tới các bài toán cần thiết như lập lịch biểu thời kì thực, chống bùng nổ tổ hợp
lúc kiếm tìm lời giải trong trí não nhân tạo, các hệ vẻ ngoài để rà soát tính đúng đắn của
chương trình trong công nghệ phần mềm, “trong không gian oxyz cho hai điểm a 1 2 3 và b 321 phương trình mặt cầu …
ví như khoa học máy tính được hiểu như trên với đối tượng nghiên cứu là máy tính và các
bí quyết tính toán trên chúng, thì khoa học tính toán (computational science) lại là khoa học
về việc dùng toán học và khoa học máy tính để làm việc trong các đơn vị quản lý khoa học khác. Dưới
tên gọi này, có rất nhiều lĩnh vực chi tiết như ngôn ngữ tính toán (computational linguistics), sinh
học tính toán (computational biology) hoặc tin sinh học (bioinformatics), vốn đầu tư tính toán
(computational finance), khoa học v
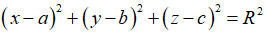
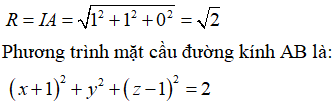



Để lại một bình luận