Phương trình mặt phẳng trung trực của đoạn thẳng – Toán Thầy Định

Phương trình mặt phẳng trung trực của đoạn thẳng trong không gian Oxyz được viết như thế nào? Bài viết dưới đây tôi sẽ hướng dẫn các bạn cách để viết phương trình một mp trung trực của đoạn thẳng trong không gian. Đồng thời tôi cũng sẽ hướng dẫn các bạn cách để nhẩm ngay được phương trình mp trung trực của đoạn thẳng. Cùng theo dõi nhé!

I. MẶT PHẲNG TRUNG TRỰC LÀ GÌ?

Trước tiên tất cả chúng ta cùng ôn lại khái niệm mặt phẳng trung trực của đoạn thẳng ( đã học từ lớp 11 ) .
Trong khoảng trống cho đoạn thẳng AB và điểm I là trung điểm của AB. Khi đó sống sót duy nhất một mặt phẳng ( P ) đi qua I và vuông góc với đoạn thẳng AB. Mặt phẳng ( P ) được gọi là mặt phẳng trung trực của đoạn thẳng AB .

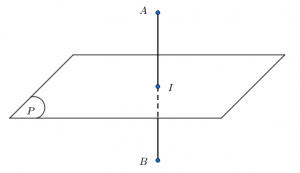
Nếu phát biểu dưới dạng quỹ tích thì mặt phẳng trung trực là quỹ tích những điểm cách đều hai điểm cho trước .
Như vậy tất cả chúng ta hoàn toàn có thể thấy khái niệm mặt phẳng trung trực cũng tựa như như khái niệm đường trung trực của đoạn thẳng trong mặt phẳng .

II. PHƯƠNG TRÌNH MẶT PHẲNG TRUNG TRỰC CỦA ĐOẠN THẲNG

Từ định nghĩa nêu trên ta hoàn toàn có thể thấy rằng nếu ( P ) là mặt phẳng trung trực của đoạn AB. Thì véc tơ AB chính là 1 véc tơ pháp tuyến của mặt phẳng ( P ). Còn trung điểm I của đoạn AB chính là 1 điểm nằm trên mặt phẳng ( P ) .
Do đó cách viết phương trình mặt phẳng trung trực ( P ) của đoạn thẳng AB như sau :

• Tính véc tơ AB là một véc tơ pháp tuyến của mặt phẳng ( P ). ( Cách tính véc tơ AB là lấy tọa độ điểm cuối B trừ đi tọa độ điểm đầu A tương ứng ) .

• Tìm tọa độ điểm I là trung điểm của đoạn thẳng AB. ( Cách tìm tọa độ trung điểm là lấy tọa độ điểm A cộng tọa độ điểm B tương ứng, xong chia cho 2 )

•  

  Viết phương trình mặt phẳng ( P ) đi qua điểm I nhận véc tơ AB là véc tơ pháp tuyến .

Ví dụ minh họa (Tự luận):

Trong khoảng trống Oxyz, cho điểm A ( 1 ; 2 ; 3 ) và điểm B ( 3 ; 6 ; 1 ). Biết mặt phẳng ( P ) là mặt phẳng trung trực của đoạn thẳng AB. Hãy viết phương trình tổng quát của ( P ) .

Lời giải:

Trung điểm I của đoạn thẳng AB có tọa độ là ( 2 ; 4 ; 2 ) .
Véc tơ AB có tọa độ ( 2 ; 4 ; − 2 ) là một véc tơ pháp tuyến của mặt phẳng ( P ) .
Do đó phương trình mặt phẳng ( P ) là :
2 ( x − 2 ) + 4 ( y − 4 ) − 2 ( z − 2 ) = 0
⇔ 2 x + 4 y − 2 z − 16 = 0
⇔ x + 2 y − z − 8 = 0 .

Bộ đề thi Online các dạng có giải chi tiết: Phương trình mặt phẳng trung trực

Ví dụ minh họa (Trắc nghiệm):

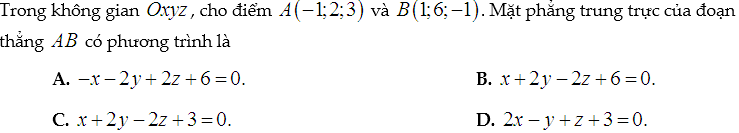
Lời giải:

Trung điểm I của đoạn thẳng AB có tọa độ là ( 0 ; 4 ; 1 ) .
Véc tơ AB có tọa độ ( 2 ; 4 ; − 4 ) là một véc tơ pháp tuyến của mặt phẳng trung trực của đoạn AB .
Vậy mặt phẳng cần tìm có phương trình là :
2 ( x − 0 ) + 4 ( y − 4 ) − 4 ( z − 1 ) = 0
⇔ x + 2 y − 2 z − 6 = 0
⇔ − x − 2 y + 2 z + 6 = 0 .
Chọn đáp án A .

III. CÁCH NHẨM NHANH PHƯƠNG TRÌNH MẶT PHẲNG TRUΝG TRỰC

Thông thường khi giám sát viết ptmp trung trực ta thường lược bớt những bước đổi khác để cho ra tác dụng ngay. Ta xét lại ví dụ bên trên :
“ Trong khoảng trống Oxyz, cho điểm A ( 1 ; 2 ; 3 ) và điểm B ( 3 ; 6 ; 1 ). Biết mặt phẳng ( P ) là mặt phẳng trung trực của đoạn thẳng AB. Hãy viết phương trình tổng quát của ( P ). ”
Ta sẽ triển khai nhẩm véc tơ AB = ( 2 ; 4 ; – 2 ). Khi đó ta sẽ viết được “ phần đầu ” của phương trình là :
2 x + 4 y – 2 z + …. = 0
Đến đây ta nhẩm tọa độ trung điểm AB là I ( 2 ; 4 ; 2 ) ta thay luôn vào “ phần đầu ” phương trình vừa tìm được. Bài nào phân số hay số to ta hoàn toàn có thể dùng tính năng CALC của máy tính để tính .
Ta được : 2.2 + 4.4 – 2.2 = 16. Ta lấy “ phần đầu ” trừ đi 16 ( hiệu quả vừa nhẩm được ) là được tác dụng :
2 x + 4 y – 2 z – 16 = 0

Trên đây là định nghĩa mặt phẳng trung trực, cách viết và cách nhẩm phương tri`nh mặt phẳng trung trực của đoạn thẳng. Các bạn hãy luyện tập để thành thạo nhé. Chúc các bạn thành công!

Xem thêm:

Góc giữa 2 vecto trong không gian

Phương Pháp Tọa Độ Oxyz –

Source: http://wp.ftn61.com
Category: Hỏi Đáp