Bài 1 – Phương trình quỹ đạo, quãng đường, vận tốc và gia tốc của chất điểm | Vật Lý Đại Cương

I. Các khái niệm cơ bản về chuyển động

1) Cơ học, động học

+ Cơ học: ngành vật lý nghiện cứu về chuyển động của các vật thể.

+ Động học: ngành vật lý nghiên cứu các tính chất, quy luật chuyển động mà không tính tới nguyên nhân của chuyển động đó.

2) Chuyển động, chất điểm

+ Chuyển động cơ học ( hoạt động ) : là sự biến hóa vị trí của những vật thể .

+ Chất điểm: là vật thể có kích thước không đáng kể so với những kích thước, khoảng cách mà ta xét.

Lưu ý : Khái niệm hoạt động, chất điểm có tính tương đối .

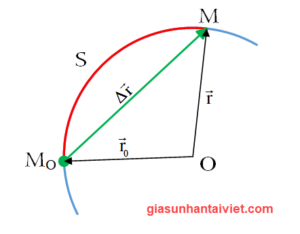
3) Quỹ đạo, quãng đường và độ dời

+ Quỹ đạo: là tập hợp các vị trí của chất điểm trong quá trình chuyển động.

+ Quãng đường: là độ dài của vết mà chất điểm vạch ra trong thời gian khảo sát chuyển động.

+ Độ dời: là vectơ nối từ vị trí đầu đến vị trí cuối.

4) Hệ quy chiếu

Là mạng lưới hệ thống gồm một vật mốc, hệ tọa độ gắn với vật mốc đó và đồng hồ đeo tay đo thời hạn, dùng để xác lập vị trí của những vật khác .

\( \vec{r}=\overrightarrow{OM}=x\overrightarrow{i}+y\overrightarrow{j}+z\overrightarrow{k} \)
\( \vec{r}=\left( x,y,z \right) \) hay \( M\left( x,y,z \right) \)

5) Phương trình chuyển động, phương trình quỹ đạo

+ Phương trình hoạt động : \ ( \ left \ { \ begin { align } và x = f ( t ) \ \ và y = g ( t ) \ \ và z = h ( t ) \ \ \ end { align } \ right. \ ) ( cho biết vị trí ở thời hạn t )+ Khử t, ta được phương trình quỹ đạo : \ ( \ left \ { \ begin { align } và F ( x, y, z ) = 0 \ \ và G ( x, y, z ) = 0 \ \ \ end { align } \ right. \ ) ( cho biết hình dạng quỹ đạo )

II. Tốc độ và vận tốc

1) Tốc độ trung bình và vận tốc trung bình

 
+ Tốc độ trung bình :

\( {{v}_{s}}={{v}_{tb}}=\bar{v}=\frac{s}{t} \)
\( {{v}_{s}}=\frac{s}{t}=\frac{{{s}_{1}}+{{s}_{2}}+…+{{s}_{n}}}{{{t}_{1}}+{{t}_{2}}+…+{{t}_{n}}} \)

+ Vận tốc trung bình :\ ( { { \ vec { v } } _ { tb } } = \ frac { \ Delta \ vec { r } } { \ Delta t } = \ frac { \ vec { r } – { { { \ vec { r } } } _ { 0 } } } { t – { { t } _ { 0 } } } \ )

2) Tốc độ tức thời và vận tốc tức thời

+ Tốc độ tức thời:

\ ( { { v } _ { s } } = \ underset { t \ to 0 } { \ mathop { \ lim } } \, \ frac { s } { t } = \ frac { ds } { dt } = s ’ \ )+ Vận tốc tức thời :\ ( \ vec { v } = \ underset { \ Delta t \ to 0 } { \ mathop { \ lim } } \, \ frac { \ Delta \ vec { r } } { \ Delta t } = \ frac { d \ vec { r } } { dt } = \ left ( { \ vec { r } } \ right ) ’ \ )⊗ Đặc điểm tức thời và tốc độ tức thời :• Phương : tiếp tuyến với quỹ đạo• Chiều : theo chiều hoạt động• Độ lớn : đạo hàm của quãng đường \ ( v = \ left | { \ vec { v } } \ right | = { { v } _ { s } } = s ’ \ )• Điểm đặt : tại điểm khảo sát

3) Ý nghĩa của tốc độ và vận tốc

+ Tốc độ là đại lượng vô hướng, không âm, đặc trưng cho tính nhanh, chậm hoạt động .+ Vận tốc là đại lượng vectơ. Vận tốc tức thời đặc trưng cho phương, chiều và độ nhanh chậm của hoạt động .+ Độ lớn của tốc độ tức thời chính là vận tốc tức thời

4) Biểu thức giải tích của vectơ vận tốc

+ Trong hệ tọa độ Descartes :

 \( \vec{r}=\overrightarrow{OM}=x\overrightarrow{i}+y\overrightarrow{j}+z\overrightarrow{k} \)
\( \vec{v}=\frac{d\vec{r}}{dt}={{v}_{x}}.\overrightarrow{i}+{{v}_{y}}.\overrightarrow{j}+{{v}_{z}}.\overrightarrow{k}=\left( {{v}_{x}},{{v}_{y}},{{v}_{z}} \right) \)

Trong đó : \ ( \ left \ { \ begin { align } và { { v } _ { x } } = \ frac { dx } { dt } = x ’ \ \ và { { v } _ { y } } = \ frac { dy } { dt } = y ’ \ \ và { { v } _ { z } } = \ frac { dz } { dt } = z ’ \ \ \ end { align } \ right. \ )+ Do đó : \ ( v = \ sqrt { v_ { x } ^ { 2 } + v_ { y } ^ { 2 } + v_ { z } ^ { 2 } } \ )

5) Tính quãng đường

Tổng quát : \ ( S = \ int \ limits_ { { { t } _ { 1 } } } ^ { { { t } _ { 2 } } } { vdx } \ )với \ ( v = \ left | { \ vec { v } } \ right | \ )Nếu v = const thì \ ( s = v \ left ( { { t } _ { 2 } } – { { t } _ { 1 } } \ right ) = v. t \ ) .

Source: http://wp.ftn61.com
Category: Hỏi Đáp