I. PHƯƠNG PHÁP GIẢI VÀ BIỆN LUẬN CÁC DẠNG PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN
Bài toán 1: Giải và biện luận phương trình: $\sin x = m.$
PHƯƠNG PHÁP CHUNG: Ta biện luận theo các bước sau:
Bước 1: Nếu $|m| > 1$ phương trình vô nghiệm.
Bước 2: Nếu $|m| \le 1$, xét hai khả năng:
+ Khả năng 1: Nếu $m$ được biểu diễn qua $\sin $ của góc đặc biệt, giả sử $\alpha $, khi đó phương trình có dạng:
$\sin x = \sin \alpha $ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = \alpha + 2k\pi }\\
{x = \pi – \alpha + 2k\pi }
\end{array}} \right.$, $k \in Z.$
+ Khả năng 2: Nếu $m$ không biểu diễn được qua $\sin $ của góc đặc biệt, khi đó đặt $m = \sin \alpha $, ta được:
$\sin x = \sin \alpha $ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = \alpha + 2k\pi }\\
{x = \pi – \alpha + 2k\pi }
\end{array}} \right.$, $k \in Z.$
Trong cả hai trường hợp ta đều kết luận phương trình có hai họ nghiệm.
Đặc biệt:
$\sin x = 0 \Leftrightarrow x = k\pi $, $k \in Z.$
$\sin x = 1 \Leftrightarrow x = \frac{\pi }{2} + 2k\pi $, $k \in Z.$
$\sin x = – 1 \Leftrightarrow x = – \frac{\pi }{2} + 2k\pi $, $k \in Z.$
Ví dụ 1: Giải các phương trình sau:
a. $\sin x = \frac{1}{3}.$
b. $\sin \left( {2x – \frac{\pi }{4}} \right) + \sin \left( {3x + \frac{\pi }{3}} \right) = 0.$
a. Đặt $\frac{1}{3} = \sin \alpha $, khi đó:
$\sin x = \sin \alpha $ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = \alpha + 2k\pi }\\
{x = \pi – \alpha + 2k\pi }
\end{array}} \right.$, $k \in Z.$
Vậy phương trình có hai họ nghiệm.
b. Ta có: $\sin \left( {2x – \frac{\pi }{4}} \right) + \sin \left( {3x + \frac{\pi }{3}} \right) = 0$ $ \Leftrightarrow \sin \left( {2x – \frac{\pi }{4}} \right) = – \sin \left( {3x + \frac{\pi }{3}} \right)$ $ \Leftrightarrow \sin \left( {2x – \frac{\pi }{4}} \right) = \sin \left( { – 3x – \frac{\pi }{3}} \right)$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{2x – \frac{\pi }{4} = – 3x – \frac{\pi }{3} + 2k\pi }\\
{2x – \frac{\pi }{4} = \pi – \left( { – 3x – \frac{\pi }{3}} \right) + 2k\pi }
\end{array}} \right.$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = – \frac{\pi }{{60}} + \frac{{2k\pi }}{5}}\\
{x = – \frac{{19\pi }}{{12}} – 2k\pi }
\end{array}} \right.$, $k \in Z.$
Vậy phương trình có hai họ nghiệm.
Ví dụ 2: Giải phương trình: $\sin (\pi \sin 2x) = 1.$
Ta có: $\sin (\pi \sin 2x) = 1$ $ \Leftrightarrow \pi \sin 2x = \frac{\pi }{2} + 2k\pi $ $ \Leftrightarrow \sin 2x = \frac{1}{2} + 2k$, $k \in Z$ $(1).$
Phương trình $(1)$ có nghiệm khi và chỉ khi:
$\left| {\frac{1}{2} + 2k} \right| \le 1$ $ \Leftrightarrow – \frac{3}{4} \le k \le \frac{1}{4}$ $ \Leftrightarrow k = 0.$
Khi đó $(1)$ có dạng:
$\sin 2x = \frac{1}{2}$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{2x = \frac{\pi }{6} + 2l\pi }\\
{2x = \frac{{5\pi }}{6} + 2l\pi }
\end{array}} \right.$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = \frac{\pi }{{12}} + l\pi }\\
{x = \frac{{5\pi }}{{12}} + l\pi }
\end{array}} \right.$, $l \in Z.$
Vậy phương trình có hai họ nghiệm.
Bài toán 2: Giải và biện luận phương trình: $\cos x = m.$
PHƯƠNG PHÁP CHUNG: Ta biện luận theo các bước sau:
Bước 1: Nếu $|m| > 1$ thì phương trình vô nghiệm.
Bước 2: Nếu $|m| \le 1$, xét hai trường hợp:
+ Khả năng 1: Nếu $m$ được biểu diễn qua $\cos $ của góc đặc biệt, giả sử $\alpha $, khi đó phương trình có dạng:
$\cos x = \cos \alpha $ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = \alpha + 2k\pi }\\
{x = – \alpha + 2k\pi }
\end{array}} \right.$, $k \in Z.$
+ Khả năng 2: Nếu $m$ không biểu diễn được qua $\cos $ của góc đặc biệt, khi đó đặt $m = \cos \alpha $, ta được:
$\cos x = \cos \alpha $ $ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{x = \alpha + 2k\pi }\\
{x = – \alpha + 2k\pi }
\end{array}} \right.$, $k \in Z.$
Trong cả hai trường hợp ta đều kết luận phương trình có hai họ nghiệm.
Đặc biệt:
$\cos x = 0 \Leftrightarrow x = \frac{\pi }{2} + k\pi $, $k \in Z.$
$\cos x = 1 \Leftrightarrow x = 2k\pi $, $k \in Z.$
$\cos x = – 1 \Leftrightarrow x = \pi + 2k\pi $, $k \in Z.$
Ví dụ 3: Giải các phương trình sau:
a. $\sin 3x = \cos 2x.$
b. $\cos \left( {2x – \frac{\pi }{4}} \right) + \sin \left( {x + \frac{\pi }{4}} \right) = 0.$
a. Ta có:
$\sin 3x = \cos 2x$ $ \Leftrightarrow \sin 3x = \sin \left( {\frac{\pi }{2} – 2x} \right)$ $ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{3x = \frac{\pi }{2} – 2x + 2k\pi }\\
{3x = \pi – \left( {\frac{\pi }{2} – 2x} \right) + 2k\pi }
\end{array}} \right.$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = \frac{\pi }{{10}} + \frac{{2k\pi }}{5}}\\
{x = \frac{\pi }{2} + 2k\pi }
\end{array}} \right.$, $k \in Z.$
Vậy phương trình có hai họ nghiệm.
b. Ta có:
$\cos \left( {2x – \frac{\pi }{4}} \right) + \sin \left( {x + \frac{\pi }{4}} \right) = 0$ $ \Leftrightarrow \cos \left( {2x – \frac{\pi }{4}} \right) = – \sin \left( {x + \frac{\pi }{4}} \right)$ $ \Leftrightarrow \cos \left( {2x – \frac{\pi }{4}} \right) = \cos \left( {x + \frac{\pi }{4} + \frac{\pi }{2}} \right)$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{2x – \frac{\pi }{4} = x + \frac{{3\pi }}{4} + 2k\pi }\\
{2x – \frac{\pi }{4} = – x – \frac{{3\pi }}{4} + 2k\pi }
\end{array}} \right.$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = \pi + 2k\pi }\\
{x = – \frac{\pi }{6} + \frac{{2k\pi }}{3}}
\end{array}} \right.$, $k \in Z.$
Vậy phương trình có hai họ nghiệm.
Ví dụ 4: Giải phương trình: $\cos \left[ {\frac{\pi }{2}\cos \left( {x – \frac{\pi }{4}} \right)} \right] = \frac{{\sqrt 2 }}{2}.$
Phương trình tương đương với:
$\left[ {\begin{array}{*{20}{l}}
{\frac{\pi }{2}\cos \left( {x – \frac{\pi }{4}} \right) = \frac{\pi }{4} + 2k\pi }\\
{\frac{\pi }{2}\cos \left( {x – \frac{\pi }{4}} \right) = – \frac{\pi }{4} + 2k\pi }
\end{array}} \right.$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{\cos \left( {x – \frac{\pi }{4}} \right) = \frac{1}{2} + 4k\:\left( 1 \right)}\\
{\cos \left( {x – \frac{\pi }{4}} \right) = – \frac{1}{2} + 4k\:\left( 2 \right)}
\end{array}} \right.$, $k \in Z.$|
Phương trình $(1)$ có nghiệm khi và chỉ khi:
$\left| {\frac{1}{2} + 4k} \right| \le 1$ $ \Leftrightarrow – \frac{3}{8} \le k \le \frac{1}{8}$ $ \Leftrightarrow k = 0.$
Khi đó $(1)$ có dạng:
$\cos \left( {x – \frac{\pi }{4}} \right) = \frac{1}{2}$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x – \frac{\pi }{4} = \frac{\pi }{3} + 2l\pi }\\
{x – \frac{\pi }{4} = – \frac{\pi }{3} + 2l\pi }
\end{array}} \right.$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = \frac{{7\pi }}{{12}} + 2l\pi }\\
{x = – \frac{\pi }{{12}} + 2l\pi }
\end{array}} \right.$, $l \in Z$ $(3).$
Phương trình $(2)$ có nghiệm khi và chỉ khi:
$\left| { – \frac{1}{2} + 4k} \right| \le 1$ $ \Leftrightarrow – \frac{1}{8} \le k \le \frac{3}{8}$ $ \Leftrightarrow k = 0.$
Khi đó $(2)$ có dạng:
$\cos \left( {x – \frac{\pi }{4}} \right) = – \frac{1}{2}$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x – \frac{\pi }{4} = \frac{{2\pi }}{3} + 2l\pi }\\
{x – \frac{\pi }{4} = – \frac{{2\pi }}{3} + 2l\pi }
\end{array}} \right.$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = \frac{{11\pi }}{{12}} + 2l\pi }\\
{x = – \frac{{5\pi }}{{12}} + 2l\pi }
\end{array}} \right.$, $l \in Z$ $(4).$
Kết hợp $(3)$ và $(4)$, ta được:
$\left[ {\begin{array}{*{20}{l}}
{x = \frac{{11\pi }}{{12}} + l\pi }\\
{x = \frac{{7\pi }}{{12}} + l\pi }
\end{array}} \right.$, $l \in Z.$
Vậy phương trình có hai họ nghiệm.
Bài toán 3: Giải và biện luận phương trình: $\tan x = m.$
PHƯƠNG PHÁP CHUNG: Ta biện luận theo các bước sau:
Đặt điều kiện:
$\cos x \ne 0 \Leftrightarrow x \ne \frac{\pi }{2} + k\pi $, $k \in Z.$
Xét hai khả năng:
+ Khả năng 1: Nếu $m$ được biểu diễn qua $\tan $ của góc đặc biệt, giả sử $\alpha $, khi đó phương trình có dạng:
$\tan x = \tan \alpha $ $ \Leftrightarrow x = \alpha + k\pi $, $k \in Z.$
+ Khả năng 2: Nếu $m$ không biểu diễn được qua $\tan $ của góc đặc biệt, khi đó đặt $m = \tan \alpha $, ta được:
$\tan x = \tan \alpha $ $ \Leftrightarrow x = \alpha + k\pi $, $k \in Z.$
Trong cả hai trường hợp ta đều kết luận phương trình có một họ nghiệm.
Nhận xét: Như vậy với mọi giá trị của tham số phương trình luôn có nghiệm.
Ví dụ 5: Giải phương trình: $\tan \left[ {\frac{\pi }{4}(\cos x + \sin x)} \right] = 1.$
Điều kiện: $\cos \left[ {\frac{\pi }{4}(\cos x + \sin x)} \right] \ne 0$ $(*).$
Phương trình tương đương với:
$\frac{\pi }{4}(\cos x + \sin x) = \frac{\pi }{4} + k\pi $ $ \Leftrightarrow \cos x + \sin x = 1 + 4k$, $k \in Z$ $(1).$
Phương trình $(1)$ có nghiệm khi và chỉ khi:
$\left| {1 + 4k} \right| \le \sqrt 2 $ $ \Leftrightarrow – \frac{{\sqrt 2 + 1}}{4} \le k \le \frac{{\sqrt 2 – 1}}{4}$ $ \Leftrightarrow k = 0.$
Khi đó $(1)$ có dạng:
$\cos x + \sin x = 1$ $ \Leftrightarrow \sqrt 2 \sin \left( {x + \frac{\pi }{4}} \right) = 1$ $ \Leftrightarrow \sin \left( {x + \frac{\pi }{4}} \right) = \frac{{\sqrt 2 }}{2}$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x + \frac{\pi }{4} = \frac{\pi }{4} + 2l\pi }\\
{x + \frac{\pi }{4} = \frac{{3\pi }}{4} + 2l\pi }
\end{array}} \right.$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = 2l\pi }\\
{x = \frac{\pi }{2} + 2l\pi }
\end{array}} \right.$, $l \in Z$ thoả mãn $(*).$
Vậy phương trình có hai họ nghiệm.
Bài toán 4: Giải và biện luận phương trình: $\cot x = m.$
PHƯƠNG PHÁP CHUNG: Ta biện luận theo các bước sau:
Đặt điều kiện:
$\sin x \ne 0 \Leftrightarrow x \ne k\pi $, $k \in Z.$
Xét hai khả năng:
+ Khả năng 1: Nếu $m$ được biểu diễn qua $\cot $ của góc đặc biệt, giả sử $\alpha $, khi đó phương trình có dạng:
$\cot x = \cot \alpha \Leftrightarrow x = \alpha + k\pi $, $k \in Z.$
+ Khả năng 2: Nếu $m$ không biểu diễn được qua $\cot $ của góc đặc biệt, khi đó đặt $m = \cot \alpha $, ta được:
$\cot x = \cot \alpha \Leftrightarrow x = \alpha + k\pi $, $k \in Z.$
Trong cả hai trường hợp ta đều kết luận phương trình có một họ nghiệm.
Nhận xét: Như vậy với mọi giá trị của tham số phương trình luôn có nghiệm.
Ví dụ 6: Giải các phương trình sau:
a. $\cot \left( {\frac{\pi }{4} – x} \right) = \frac{1}{{\sqrt 3 }}.$
b. $\cos x = \sqrt 3 \sin x.$
a. Điều kiện:
$\sin \left( {\frac{\pi }{4} – x} \right) \ne 0$ $ \Leftrightarrow \frac{\pi }{4} – x \ne k\pi $ $ \Leftrightarrow x \ne \frac{\pi }{4} – k\pi $, $k \in Z$ $(*).$
Ta có:
$\cot \left( {\frac{\pi }{4} – x} \right) = \cot \frac{\pi }{3}$ $ \Leftrightarrow \frac{\pi }{4} – x = \frac{\pi }{3} + k\pi $ $ \Leftrightarrow x = – \frac{\pi }{{12}} – k\pi $, $k \in Z$ thoả mãn điều kiện $(*).$
Vậy phương trình có một họ nghiệm.
b. Ta có:
$\cos x = \sqrt 3 \sin x$ $ \Leftrightarrow \cot x = \sqrt 3 = \cot \frac{\pi }{6}$ $ \Leftrightarrow x = \frac{\pi }{6} + k\pi $, $k \in Z.$
Vậy phương trình có một họ nghiệm.
Bài toán 5: Biện luận theo $m$ số nghiệm thuộc $(\alpha ,\beta )$ của phương trình lượng giác cơ bản.
PHƯƠNG PHÁP CHUNG: Giả sử với phương trình: $\sin x = m.$
Ta lựa chọn một trong hai cách sau:
Cách 1: Thực hiện theo các bước sau:
+ Bước 1: Biểu diễn $(\alpha ,\beta )$ trên đường tròn đơn vị thành cung $\widehat {AB}.$
+ Bước 2: Tịnh tiến đường thẳng $m$ song song với trục cosin, khi đó số giao điểm của nó với cung $\widehat {AB}$ bằng số nghiệm thuộc $(\alpha ,\beta )$ của phương trình.
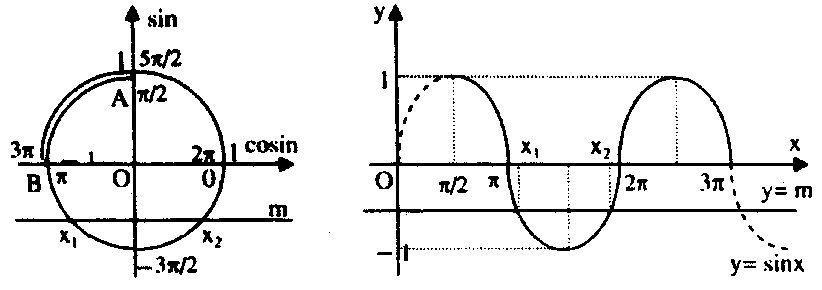
Cách 2: Thực hiện theo các bước sau:
+ Bước 1: Vẽ đồ thị hàm số $y = \sin x$, lấy trên $(\alpha ,\beta ).$
+ Bước 2: Tịnh tiến đường thẳng $y = m$ song song với trục $Ox$, khi đó số giao điểm của nó với phần đồ thị hàm số $y = \sin x$ bằng số nghiệm thuộc $(\alpha ,\beta )$ của phương trình.
Chú ý: Phương pháp trên được mở rộng tự nhiên cho:
1. Phương trình $\cos x = m$, với lưu ý khi sử dụng cách 1 ta tịnh tiến đường thẳng $m$ song song với trục sin.
2. Với các phương trình $\tan x = m$ và $\cot x = m$ ta chỉ có thể sử dụng cách 2.
Ví dụ 7: Biện luận theo $m$ số nghiệm thuộc $\left( {\frac{\pi }{6},\frac{{8\pi }}{3}} \right)$ của phương trình $\sin x = m.$
Ta lựa chọn một trong hai cách màn biểu diễn :
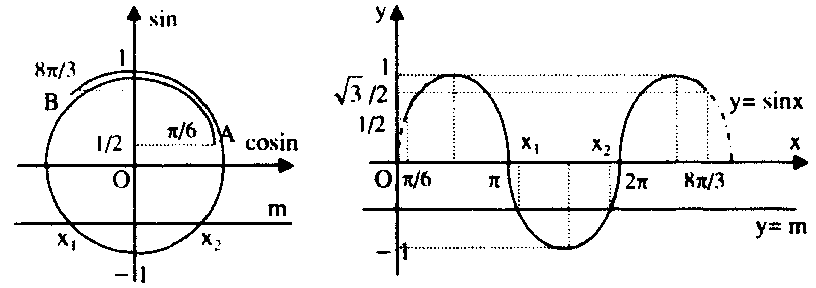
Kết luận: đặt $D = \left( {\frac{\pi }{6},\frac{{8\pi }}{3}} \right)$, ta có:
+ Với $|m| > 1$, phương trình vô nghiệm.
+ Với $m =-1$, phương trình có một nghiệm thuộc $D.$
+ Với $ – 1 < m < \frac{1}{2}$ hoặc $m=1$, phương trình có hai nghiệm phân biệt thuộc $D.$
+ Với $\frac{1}{2} \le m < \frac{{\sqrt 3 }}{2}$, phương trình có ba nghiệm phân biệt thuộc $D.$
+ Với $\frac{{\sqrt 3 }}{2} \le m < 1$, phương trình có bốn nghiệm phân biệt thuộc $D.$
Ví dụ 8: Biện luận theo $m$ số nghiệm thuộc $\left( { – \frac{{5\pi }}{4},\pi } \right)$ của phương trình: $(m + 1)\sin x = (m – 1)\cos x$ $(1).$
Biến đổi phương trình về dạng:
$\sin x + \cos x = m(\cos x – \sin x)$ $ \Leftrightarrow \sqrt 2 \sin \left( {x + \frac{\pi }{4}} \right) = m\sqrt 2 \cos \left( {x + \frac{\pi }{4}} \right)$ $ \Leftrightarrow \tan \left( {x + \frac{\pi }{4}} \right) = m.$
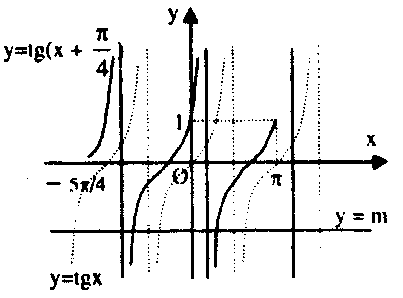
Ta có kết luận:
+ Với $m \ge 1$ hoặc $m \le 0$, phương trình có hai nghiệm phân biệt thuộc $D.$
+ Với $0 < m < 1$, phương trình có ba nghiệm phân biệt thuộc $D.$
II. CÁC BÀI TOÁN THI
Bài 1: (ĐHSP II – 2000): Tìm các nghiệm nguyên của phương trình:
$\cos \left[ {\frac{\pi }{8}\left( {3x – \sqrt {9{x^2} + 160x + 800} } \right)} \right] = 1.$
Biến đổi tương đương phương trình về dạng:
$\frac{\pi }{8}\left( {3x – \sqrt {9{x^2} + 160x + 800} } \right) = 2k\pi $ $ \Leftrightarrow \sqrt {9{x^2} + 160x + 800} = 3x – 16k$ $ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{3x – 16k \ge 0}\\
{9{x^2} + 160x + 800 = {{(3x – 16k)}^2}}
\end{array}} \right.$ $ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{x \ge \frac{{16k}}{3},k \in Z}\\
{(3k + 5)x = 8{k^2} – 25}
\end{array}} \right.$ $ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{\frac{{8{k^2} – 25}}{{3k + 5}} \ge \frac{{16k}}{3},k \in Z}\\
{x = \frac{{8{k^2} – 25}}{{3k + 5}}}
\end{array}} \right.$ $ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{k < – \frac{5}{3},k \in Z\:\left( 1 \right)}\\
{9x = 24k – 40 – \frac{{25}}{{3k + 5}}\:\left( 2 \right)}
\end{array}} \right..$
Muốn $x$ nguyên thì trước hết từ $(2)$ ta phải có:
$\frac{{25}}{{3k + 5}} \in Z$ $ \Leftrightarrow 3k + 5$ là ước của $25$ $\mathop \Leftrightarrow \limits^{\left( 1 \right)} \left[ {\begin{array}{*{20}{l}}
{3k + 5 = – 1}\\
{3k + 5 = – 5}\\
{3k + 5 = – 25}
\end{array}} \right.$ $\mathop \Leftrightarrow \limits^{k \in Z} \left[ {\begin{array}{*{20}{l}}
{k = – 2}\\
{k = – 10}
\end{array}} \right..$
+ Với $k = – 2$, ta được $x= – 7.$
+ Với $k = -10$, ta được $x = -31.$
Vậy phương trình có hai nghiệm nguyên $x = -7$ và $x = – 31.$
Bài 2: (Đại học tổng hợp Lômônốp – 1982): Giải phương trình:
$\sqrt { – {x^8} + 3{x^4} – 2} .\sin \left[ {\pi \left( {16{x^2} + 2x} \right] = 0} \right..$
Biến đổi tương đương phương trình về dạng:
$\left[ {\begin{array}{*{20}{l}}
{ – {x^8} + 3{x^4} – 2 = 0\:\left( 1 \right)}\\
{\left\{ {\begin{array}{*{20}{l}}
{ – {x^8} + 3{x^4} – 2 > 0\:\left( 2 \right)}\\
{\sin \left[ {\pi \left( {16{x^2} + 2x} \right)} \right] = 0\:\left( 3 \right)}
\end{array}} \right.}
\end{array}} \right.$
Giải $(1)$ bằng cách đặt $t = {x^4}$, điều kiện $t \ge 0$, ta được:
$(1) \Leftrightarrow {t^2} – 3t + 2 = 0$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{t = 1}\\
{t = 2}
\end{array}} \right.$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{{x^4} = 1}\\
{{x^4} = 2}
\end{array}} \right.$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = \pm 1}\\
{x = \pm \sqrt[4]{2}}
\end{array}} \right..$
Giải $(2)$, dựa vào lời giải của $(1)$ ta được:
$(2) \Leftrightarrow 1 < t < 2$ $ \Leftrightarrow 1 < {x^4} < 2$ $ \Leftrightarrow 1 < |x| < \sqrt[4]{2}$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{ – \sqrt[4]{2} < x < – 1}\\
{1 < x < \sqrt[4]{2}}
\end{array}} \right..$
Giải $(3)$, ta có:
$(3) \Leftrightarrow \pi \left( {16{x^2} + 2x} \right) = k\pi $ $ \Leftrightarrow 16{x^2} + 2x – k = 0$ $(4).$
Phương trình $(4)$ có nghiệm khi:
$\Delta’ \ge 0$ $ \Leftrightarrow 1 + 16k \ge 0$ $ \Leftrightarrow k \ge – \frac{1}{{16}}$ $\mathop \Leftrightarrow \limits^{k \in Z} k \ge 0.$
Khi đó $(4)$ có nghiệm: ${x_{1,2}} = \frac{{ – 1 \pm \sqrt {1 + 16k} }}{{16}}.$
Để nghiệm ${x_1} = \frac{{ – 1 + \sqrt {1 + 16k} }}{{16}}$ $( \ge 0)$ thoả mãn $(2)$ điều kiện là:
$1 < \frac{{ – 1 + \sqrt {1 + 16k} }}{{16}} < \sqrt[4]{2}$ $ \Leftrightarrow 17 < \sqrt {1 + 16k} < 1 + 16\sqrt[4]{2}$ $ \Leftrightarrow 18 < k < 16\sqrt 2 + 2\sqrt[4]{2}$ $\mathop \Leftrightarrow \limits^{k \in Z} k = \{ 19,20,21,22,23,24,25\} .$
Để nghiệm ${x_2} = \frac{{ – 1 – \sqrt {1 + 16k} }}{{16}}$ $(<0)$ thoả mãn $(2)$ điều kiện là:
$ – \sqrt[4]{2} < \frac{{ – 1 – \sqrt {1 + 16k} }}{{16}} < – 1$ $ \Leftrightarrow 15 < \sqrt {1 + 16k} < 16\sqrt[4]{2} – 1$ $ \Leftrightarrow 14 < k < 16\sqrt 2 – 2\sqrt[4]{2}$ $\mathop \Leftrightarrow \limits^{k \in Z} k = \{ 15,16,17,18,19,20\} .$
Vậy phương trình có các nghiệm:
$x = \left\{ { \pm 1, \pm \sqrt[4]{2}} \right\}$ $ \cup \left\{ {x = \frac{{ – 1 + \sqrt {1 + 16k} }}{{16}}|k = \overline {19,25} } \right\}$ $ \cup \left\{ {x = \frac{{ – 1 – \sqrt {1 + 16k} }}{{16}}|k = \overline {15,20} } \right\}.$
Bài 3: Giải và biện luận phương trình: $\frac{{{a^2}}}{{1 – {{\tan }^2}x}} = \frac{{{{\sin }^2}x + {a^2} – 2}}{{\cos 2x}}.$
Điều kiện:
$\left\{ {\begin{array}{*{20}{l}}
{\cos x \ne 0}\\
{1 – {{\tan }^2}x \ne 0}\\
{\cos 2x \ne 0}
\end{array}} \right.$ $ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{\cos x \ne 0}\\
{1 – {{\tan }^2}x \ne 0}
\end{array}} \right.$ $ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{\cos x \ne 0}\\
{\tan x \ne \pm 1}
\end{array}} \right.$ $ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{x \ne \frac{\pi }{2} + k\pi }\\
{x \ne \pm \frac{\pi }{4} + k\pi }
\end{array}} \right.$, $k \in Z.$
Biến đổi phương trình về dạng:
$\frac{{{a^2}}}{{1 – {{\tan }^2}x}} = \frac{{{{\sin }^2}x + {a^2} – 2}}{{{{\cos }^2}x – {{\sin }^2}x}}$ $ \Leftrightarrow \frac{{{a^2}}}{{1 – {{\tan }^2}x}} = \frac{{{{\tan }^2}x + \left( {{a^2} – 2} \right)\left( {1 + {{\tan }^2}x} \right)}}{{1 – {{\tan }^2}x}}$ $ \Leftrightarrow \left( {{a^2} – 1} \right){\tan ^2}x = 2$ $(1).$
Với ${a^2} – 1 = 0 \Leftrightarrow a = \pm 1$, khi đó $(1)$ vô nghiệm.
Với ${a^2} – 1 \ne 0 \Leftrightarrow a \ne \pm 1$, khi đó $(1)$ có dạng:
${\tan ^2}x = \frac{2}{{{a^2} – 1}}$ $(2).$
Để $(2)$ có nghiệm và thoả mãn điều kiện ta cần có:
$\left\{ {\begin{array}{*{20}{l}}
{\frac{2}{{{a^2} – 1}} \ge 0}\\
{\frac{2}{{{a^2} – 1}} \ne 1}
\end{array}} \right.$ $ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{|a| > 1}\\
{a \ne \pm \sqrt 3 }
\end{array}} \right..$
Khi đó: $(2) \Leftrightarrow \tan x = \pm \tan \alpha $ $ \Leftrightarrow x = \pm \alpha + k\pi $, $k \in Z.$
Kết luận:
+ Với $|a| \le 1$ hoặc $a = \pm \sqrt 3 $, phương trình vô nghiệm.
+ Với $a \in ( – \infty, – 1) \cup (1, + \infty )\backslash \left\{ { \pm \sqrt 3 } \right\}$, phương trình có hai họ nghiệm.
III. BÀI TẬP ĐỀ NGHỊ
Bài tập 1: Giải các phương trình sau:
a. $\sin (\pi \cos 2x) = 1.$
b. $\cos (\pi \cos 3x) = 1.$
Bài tập 2: Giải các phương trình sau:
a. $\cos (\pi \sin x) = 1.$
b. $\sin \frac{\pi }{x} = \cos (\pi x).$
c. $\cos \left[ {\frac{\pi }{2}\cos \left( {x – \frac{\pi }{4}} \right)} \right] = \frac{1}{2}.$
Bài tập 3: Giải các phương trình sau:
a. $\tan \left[ {\frac{\pi }{4}(\cos x – \sin x)} \right] = 1.$
b. $\cot \left[ {\frac{\pi }{4}(\cos x + \sin x)} \right] = 1.$
Bài tập 4: Giải và biện luận các phương trình sau:
a. $\cos (x + \alpha ) + \cos (x – \alpha ) = 2\cos \alpha .$
b. $\sin (x + \alpha ) + \cos (x – \alpha ) = 1 + \sin \alpha .$
c. $(m + 1)\sin 2x + 1 – {m^2} = 0.$
d. $(m + 2)\tan 2x – \sqrt m = 0.$
Bài tập 5: Biện luận theo $m$ số nghiệm của phương trình:
a. $\sin x = m$ với $x \in \left( { – \frac{\pi }{4},\frac{{4\pi }}{3}} \right].$
b. $\sin \left( {2x – \frac{\pi }{4}} \right) = m$ với $x \in \left[ { – \frac{\pi }{{24}},\frac{{19\pi }}{8}} \right].$
c. $\cos \left( {x – \frac{\pi }{3}} \right) = m$ với $x \in \left[ {\frac{{5\pi }}{6},\frac{{13\pi }}{6}} \right].$
d. $\cot \left( {x – \frac{\pi }{4}} \right) = m$ với $x \in \left( { – \frac{{5\pi }}{4},\pi } \right).$
Source: http://wp.ftn61.com
Category: Hỏi Đáp



Để lại một bình luận