Phương trình tích: Định nghĩa, Bài tập và Cách giải phương trình tích

Phương trình tích là một dạng toán cơ bản trong chương trình toán lớp 8, lớp 9. Vậy cụ thể phương trình tích là gì? Kiến thức cần nắm phương trình tích lớp 8, lớp 9? Lý thuyết và bài tập về phương trình tích?… Trong bài viết dưới đây, DINHNGHIA.VN sẽ giúp bạn tổng hợp kiến thức về chủ đề trên, cùng tìm hiểu nhé!

Tìm hiểu phương trình tích là gì?

Định nghĩa phương trình tích 

Phương trình tích là những phương trình mà một vế là tích của những đa thức còn một vế bằng \ ( 0 \ )

Ví dụ: \( (x^2-x+2)(x-3)=0 \)

Dạng tổng quát phương trình tích

\ ( f_1 ( x ). f_2 ( x ) … f_n ( x ) = 0 \ ) với \ ( f_i ( x ) \ ) là những hàm số của \ ( x \ )
Nghiệm của phương trình là hợp của tập nghiệm của từng phương trình \ ( f_i ( x ) = 0 \ ) với \ ( i = 1,2, … n \ )

Cách giải phương trình tích

Để giải những dạng toán về chủ đề này thì cách chung là tất cả chúng ta sẽ đổi khác vế trái để quy về dạng tích của những hàm số. Để đổi khác được thì tất cả chúng ta cần nắm vững một số ít chiêu thức nghiên cứu và phân tích đa thức thành nhân tử .

Phương pháp đặt nhân tử chung

Bài toán: \( A(x) +B(x) =0 \)

Các bước làm :

• Bước 1 : Biến đổi \ ( A ( x ) = C ( x ). A_1 ( x ) \ ) ; \ ( B ( x ) = C ( x ). B_1 ( x ) \ )
• Bước 2 : Khi đó ta có : \ ( A ( x ) + B ( x ) = C ( x ) [ A_1 ( x ) + B_1 ( x ) ] \ )
• Bước 3 : Giải từng phương trình \ ( C ( x ) = 0 \ ) và \ ( A_1 ( x ) + B_1 ( x ) = 0 \ )

Ví dụ:

Giải phương trình : \ ( x ^ 2-4 + \ frac { x-2 } { 3 } = 0 \ )

Cách giải:

Phương trình đã cho tương tự với :
\ ( ( x-2 ) ( x + 2 ) + \ frac { x-2 } { 3 } = 0 \ )
\ ( \ Leftrightarrow ( x-2 ) ( x + 2 + \ frac { 1 } { 3 } ) = 0 \ )
\ ( \ Leftrightarrow \ left [ \ begin { array } { l } x = 2 \ \ x = – \ frac { 7 } { 3 } \ end { array } \ right. \ )

Phương pháp sử dụng hằng đẳng thức

Để sử dụng giải pháp này tất cả chúng ta cần nắm vững bảy hằng đẳng thức đáng nhớ :

Ngoài ra tất cả chúng ta nên ghi nhớ thêm 1 số ít đẳng thức thường gặp :
\ ( a ^ 4 – b ^ 4 = ( a ^ 2 + b ^ 2 ) ( a-b ) ( a + b ) \ )
\ ( ( a + b + c ) ^ 2 = a ^ 2 + b ^ 2 + c ^ 2 + 2 ab + 2 bc + 2 ac \ )
\ ( ( a + b + c ) ^ 3 = a ^ 3 + b ^ 3 + c ^ 3 + 3 ( a + b ) ( b + c ) ( c + a ) \ )
\ ( ( a + b ) ( b + c ) ( c + a ) = ( a + b + c ) ( ab + bc + ca ) – abc \ )

Ví dụ:

Giải phương trình : \ ( x ^ 2 + 4 x + 4 – \ sqrt { 2 x + 1 } – ( x-1 ) ^ 2 = 0 \ )

Cách giải:

ĐKXĐ : \ ( x \ geq \ frac { – 1 } { 2 } \ )
Phương trình đã cho tương tự với :
\ ( \ Leftrightarrow ( x + 2 ) ^ 2 – ( x-1 ) ^ 2 – \ sqrt { 2 x + 1 } = 0 \ )
\ ( \ Leftrightarrow 3 ( 2 x + 1 ) – \ sqrt { 2 x + 1 } = 0 \ )
\ ( \ Leftrightarrow \ sqrt { 2 x + 1 }. ( 3 – \ sqrt { 2 x + 1 } ) = 0 \ )
\ ( \ Leftrightarrow \ left [ \ begin { array } { l } 2 x + 1 = 0 \ \ 3 = \ sqrt { 2 x + 1 } \ end { array } \ right. \ )
\ ( \ Leftrightarrow \ left [ \ begin { array } { l } x = \ frac { – 1 } { 2 } \ \ x = 4 \ end { array } \ right. \ )

Phương pháp tách, thêm bớt để xuất hiện nhân tử chung

Cơ sở của giải pháp này là tất cả chúng ta sử dụng định lý sau :
Nếu \ ( x = a \ ) là một nghiệm của phương trình \ ( f ( x ) = 0 \ ) thì ta luôn hoàn toàn có thể viết \ ( f ( x ) \ ) dưới dạng \ ( f ( x ) = ( x-a ). g ( x ) \ )
Như vậy ở những bài toán phương trình tích thì tất cả chúng ta cần nhẩm được nghiệm nguyên \ ( a \ ) của phương trình rồi từ đó tách, ghép để làm Open nhân tử \ ( ( x-a ) \ )

Phương pháp tách 

Bài toán : \ ( A ( x ) + B ( x ) + C ( x ) = 0 \ )
Cách làm như sau : Chúng ta tách \ ( C ( x ) = C_1 ( x ) + C_2 ( x ) \ ) hài hòa và hợp lý sao cho \ ( [ A ( x ) + C_1 ( x ) ] \ ) và \ ( [ B ( x ) + C_2 ( x ) ] \ ) có nhân tử chung

Ví dụ:

Giải phương trình \ ( 5 x ^ 3-7 x + 2 = 0 \ )

Cách giải:

Nhẩm nghiệm thấy \ ( x = 1 \ ) là nghiệm của phương trình nên ta cần tách để làm Open nhân tử \ ( ( x-1 ) \ )
Phương trình đã cho tương tự với
\ ( 5 x ^ 3-5 x – 2 x + 2 = 0 \ )
\ ( \ Leftrightarrow 5 x ( x ^ 2-1 ) – 2 ( x-1 ) = 0 \ )
\ ( \ Leftrightarrow 5 x ( x + 1 ) ( x-1 ) – 2 ( x-1 ) = 0 \ )
\ ( \ Leftrightarrow ( 5 x ^ 2 + 5 x – 2 ) ( x-1 ) = 0 \ )
\ ( \ Leftrightarrow \ left [ \ begin { array } { l } 5 x ^ 2 + 5 x – 2 = 0 \ \ x = 1 \ end { array } \ right. \ )
\ ( \ Leftrightarrow \ left [ \ begin { array } { l } x = \ frac { – 1 – \ frac { \ sqrt { 13 } } { 5 } } { 2 } \ \ x = \ frac { 1 – \ frac { \ sqrt { 13 } } { 5 } } { 2 } \ \ x = 1 \ end { array } \ right. \ )

Phương pháp thêm bớt

Bài toán: \( A(x)+B(x)=0 \)

Cách làm như sau : Chúng ta thêm vào \ ( A ( x ) \ ) một đại lượng \ ( C ( x ) \ ) rồi bớt đi ở \ ( B ( x ) \ ) đại lượng \ ( C ( x ) \ ) sao cho \ ( A ( x ) + C ( x ) \ ) và \ ( B ( x ) – C ( x ) \ ) có nhân tử chung

Ví dụ:

Giải phương trình : \ ( x ^ 3 – x ^ 2-4 = 0 \ )

Cách giải:

Nhẩm nghiệm thấy \ ( x-2 \ ) là nghiệm của phương trình nên ta thêm bớt để làm Open nhân tử \ ( ( x-2 ) \ )
Phương trình đã cho tương tự với
\ ( x ^ 3-2 x ^ 2 + x ^ 2-2 x + 2 x – 4 = 0 \ )
\ ( \ Leftrightarrow x ^ 2 ( x-2 ) + x ( x-2 ) + 2 ( x-2 ) = 0 \ )
\ ( \ Leftrightarrow ( x-2 ) ( x ^ 2 + x + 2 ) = 0 \ )
\ ( \ Leftrightarrow \ left [ \ begin { array } { l } x = 2 \ \ x ^ 2 + x + 2 = 0 \ end { array } \ right. \ )
Mặt khác \ ( x ^ 2 + x + 2 = ( x + \ frac { 1 } { 2 } ) ^ 2 + \ frac { 7 } { 4 } > 0 \ hspace { 1 cm } \ forall x \ in \ mathbb { R } \ )
Vậy phương trình đã cho có nghiệm duy nhất \ ( x = 2 \ )
Chú ý : Hầu hết trong những bài toán phương trình tích có nghiệm nguyên thì chúng cần nhẩm được nghiệm của phương trình đó rồi từ đó sử dụng những giải pháp hài hòa và hợp lý để làm Open nhân tử chung .

Tìm hiểu bất phương trình tích là gì?

Định nghĩa bất phương trình tích

Tương tự như phương trình tích thì bất phương trình tích là những bất phương trình có một vế là tích của những đa thức còn một vế bằng \ ( 0 \ ). Dấu của bất phương trình hoàn toàn có thể là \ ( >, < \ ) hoặc \ ( \ leq, \ geq \ )

Dạng tổng quát bất phương trình tích

\ ( f_1 ( x ). f_2 ( x ) … f_n ( x ) > 0 \ )

Phương pháp giải:

• Bước 1 : Sử dụng những chiêu thức nghiên cứu và phân tích nhân tử để đổi khác đưa bất phương trình về dạng như trên
• Bước 2 : Tìm nghiệm của từng hàm số \ ( f_1 ( x ) ; f_2 ( x ) ; … ; f_n ( x ) \ )
• Bước 3 : Lập bảng xét dấu và tìm tập hợp nghiệm của bất phương trình

Ví dụ:

Giải bất phương trình : \ ( 2 x ^ 2 – ( x-1 ) \ sqrt { x + 1 } – 2 \ geq 0 \ )

Cách giải:

ĐKXĐ : \ ( x \ geq – 1 \ )
Bất phương trình đã cho tương tự với :
\ ( 2 ( x ^ 2-1 ) – ( x-1 ) \ sqrt { x + 1 } \ geq 0 \ )
\ ( \ Leftrightarrow 2 ( x-1 ) ( x + 1 ) – ( x-1 ) \ sqrt { x + 1 } \ geq 0 \ )
\ ( \ Leftrightarrow ( x-1 ) \ sqrt { x + 1 } ( 2 – \ sqrt { x + 1 } ) \ geq 0 \ )
Ta có bảng xét dấu sau :

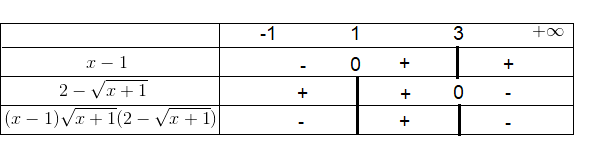
Bài tập về phương trình tích nâng cao

Phương pháp đặt ẩn phụ

Trong một số ít bài toán phức tạp, tất cả chúng ta đặt ẩn phụ \ ( y = f ( x ) \ ) thích hợp rồi sau đó nghiên cứu và phân tích nhân tử với hàm số hai ẩn \ ( x ; y \ ). Sau khi nghiên cứu và phân tích nhân tử xong tất cả chúng ta thay \ ( y \ ) bởi \ ( f ( x ) \ ) vào phương trình tích thu được .

Ví dụ:

Giải phương trình : \ ( x \ sqrt { x } – \ sqrt { x } \ sqrt { x + 1 } + \ sqrt { x } – x \ sqrt { x + 1 } + x + 2-2 \ sqrt { x + 1 } = 0 \ )

Cách giải:

ĐKXĐ : \ ( x \ geq 0 \ )
Ta có phương trình tương tự với :
\ ( \ Leftrightarrow x \ sqrt { x } – \ sqrt { x } ( \ sqrt { x + 1 } – 1 ) – x ( \ sqrt { x + 1 } – 1 ) + ( x + 1 ) – 2 \ sqrt { x + 1 } + 1 = 0 \ )
\ ( \ Leftrightarrow x \ sqrt { x } – \ sqrt { x } ( \ sqrt { x + 1 } – 1 ) – x ( \ sqrt { x + 1 } – 1 ) + ( \ sqrt { x + 1 } – 1 ) ^ 2 = 0 \ )
Đặt \ ( \ sqrt { x + 1 } – 1 = y \ ). Thay vào phương trình đã cho ta có :
\ ( x \ sqrt { x } – \ sqrt { x } y-xy + y ^ 2 = 0 \ )
\ ( \ Leftrightarrow \ sqrt { x } ( x-y ) – y ( x-y ) = 0 \ )
\ ( \ Leftrightarrow ( x-y ) ( \ sqrt { x } – y ) = 0 \ )
Thay \ ( \ sqrt { x + 1 } – 1 = y \ ) vào ta có :
\ ( ( x + 1 – \ sqrt { x + 1 } ) ( \ sqrt { x } + 1 – \ sqrt { x + 1 } ) = 0 \ )
\ ( \ Leftrightarrow \ sqrt { x + 1 } ( \ sqrt { x + 1 } – 1 ) ( \ sqrt { x } + 1 – \ sqrt { x + 1 } ) = 0 \ )
Ta có :
\ ( \ sqrt { x + 1 } = 0 \ Leftrightarrow x = – 1 \ ) ( loại )
\ ( \ sqrt { x + 1 } – 1 = 0 \ Leftrightarrow x = 0 \ ) ( thỏa mãn nhu cầu )
\ ( \ sqrt { x } + 1 – \ sqrt { x + 1 } = 0 \ Rightarrow x + 1 + 2 \ sqrt { x } = x + 1 \ )
\ ( \ Leftrightarrow 2 \ sqrt { x } = 0 \ Leftrightarrow x = 0 \ ) ( thỏa mãn nhu cầu )
Vậy phương trình đã cho có nghiệm suy nhất \ ( x = 0 \ )

Phương pháp hệ số bất định

Phương pháp này thường được sử dụng để giải những phương trình bậc \ ( 4 \ ) mà ta không nhẩm được nghiệm nguyên. Nguyên lý của chiêu thức này như sau :
Nếu hàm số bậc \ ( 4 \ ) nghiên cứu và phân tích được thành nhân tử thì nó sẽ nghiên cứu và phân tích được dưới dạng \ ( ( k_1x ^ 2 + ax + b ) ( k_2x ^ 2 + cx + d ) \ )
Thường trong những bài toán thì \ ( k_1 = k_2 = 1 \ ). Khi đó khai triển ta được
\ ( ( x ^ 2 + ax + b ) ( x ^ 2 + cx + d ) = x ^ 4 + ( a + c ) x ^ 3 + ( ac + b + d ) x ^ 2 + ( ad + bc ) c + bd \ )
Như vậy với hàm số bậc \ ( 4 \ ) cho trước thì ta hoàn toàn có thể như nhau những thông số của từng hạng tử chứa \ ( x \ ) rồi giải hệ để tìm ra \ ( a, b, c, d \ ) rồi từ đó nghiên cứu và phân tích được thành nhân tử
Chú ý : Nếu \ ( k_1. k_2 \ neq 1 \ ) thì tất cả chúng ta khai triển gồm cả \ ( k_1 ; k_2 \ ) rồi giải hệ tìm \ ( k_1 ; k_2 \ )
Trong những bài toán thường thì những thông số \ ( a ; b ; c ; d \ ) là những số nguyên

Ví dụ:

Giải phương trình : \ ( x4 – 6 x ^ 3 + 12 x ^ 2 – 14 x + 3 = 0 \ )

Cách giải:

Giả sử ta nghiên cứu và phân tích được vế trái dưới dạng
\ ( ( x ^ 2 + ax + b ) ( x ^ 2 + cx + d ) \ )
Khi đó ta có :
\ ( x ^ 4 – 6 x ^ 3 + 12 x ^ 2 – 14 x + 3 = x ^ 4 + ( a + c ) x ^ 3 + ( ac + b + d ) x ^ 2 + ( ad + bc ) c + bd \ )
Đồng nhất thông số ta được
\ ( \ left \ { \ begin { matrix } a + c = – 6 \ \ ac + b + d = 12 \ \ ad + bc = – 14 \ \ bd = 3 \ end { matrix } \ right. \ )
Vì \ ( bd = 3 \ ) nên ta chọn \ ( b = 1 ; d = 3 \ )
Khi đó :
\ ( \ left \ { \ begin { matrix } a + c = – 6 \ \ ac = 8 \ \ 3 a + c = – 14 \ end { matrix } \ right. \ )
\ ( \ left \ { \ begin { matrix } a = – 4 \ \ c = – 2 \ end { matrix } \ right. \ )
Vậy \ ( \ left \ { \ begin { matrix } a = – 4 \ \ b = 1 \ \ c = – 2 \ \ d = 1 \ end { matrix } \ right. \ )
Như vậy phương trình đã cho tương tự với
\ ( ( x ^ 2-4 x + 1 ) ( x ^ 2-2 x + 3 ) = 0 \ )
Ta có :
\ ( x ^ 2-4 x + 1 = 0 \ Leftrightarrow \ left [ \ begin { array } { l } x = 2 – \ sqrt { 3 } \ \ x = 2 + \ sqrt { 3 } \ end { array } \ right. \ )
\ ( x ^ 2-2 x + 3 = ( x-1 ) ^ 2 + 2 > 0 \ hspace { 1 cm } \ forall x \ in \ mathbb { R } \ )
Vậy phương trình đã cho có nghiệm \ ( x = 2 – \ sqrt { 3 } \ ) hoặc \ ( x = 2 + \ sqrt { 3 } \ )

Bài viết trên đây của DINHNGHIA.VN đã giúp bạn tổng hợp lý thuyết về phương trình tích, bất phương trình tích cũng như phương pháp giải một số dạng toán cơ bản và nâng cao. Hy vọng những kiến thức trong bài viết sẽ giúp ích cho bạn trong quá trình học tập và nghiên cứu về chủ đề phương trình tích. Chúc bạn luôn học tốt!

Xem thêm >>> Định lý Talet trong tam giác, trong hình thang

Rate this post

Please follow and like us :

Source: http://wp.ftn61.com
Category: Hỏi Đáp