Ba ngàn năm trước Công Nguyên, một viên quan dưới thời Babylon cổ đại đến gặp người nông dân và nói rằng thuế lúa mì của mùa vụ này sẽ tăng lên. Lẽ dĩ nhiên, những người nông dân sẽ phải tăng diện tích thửa ruộng của mình để có thể nộp thêm thuế.
Khi một trong số họ muốn mở rộng cả chiều dài và chiều rộng thửa ruộng ra cùng một khoảng bằng x, người nông dân này vấp phải một phương trình dạng: Ax2 Bx C = 0. Đó có thể là lần đầu tiên mà con người phải đối mặt với một phương trình bậc hai.
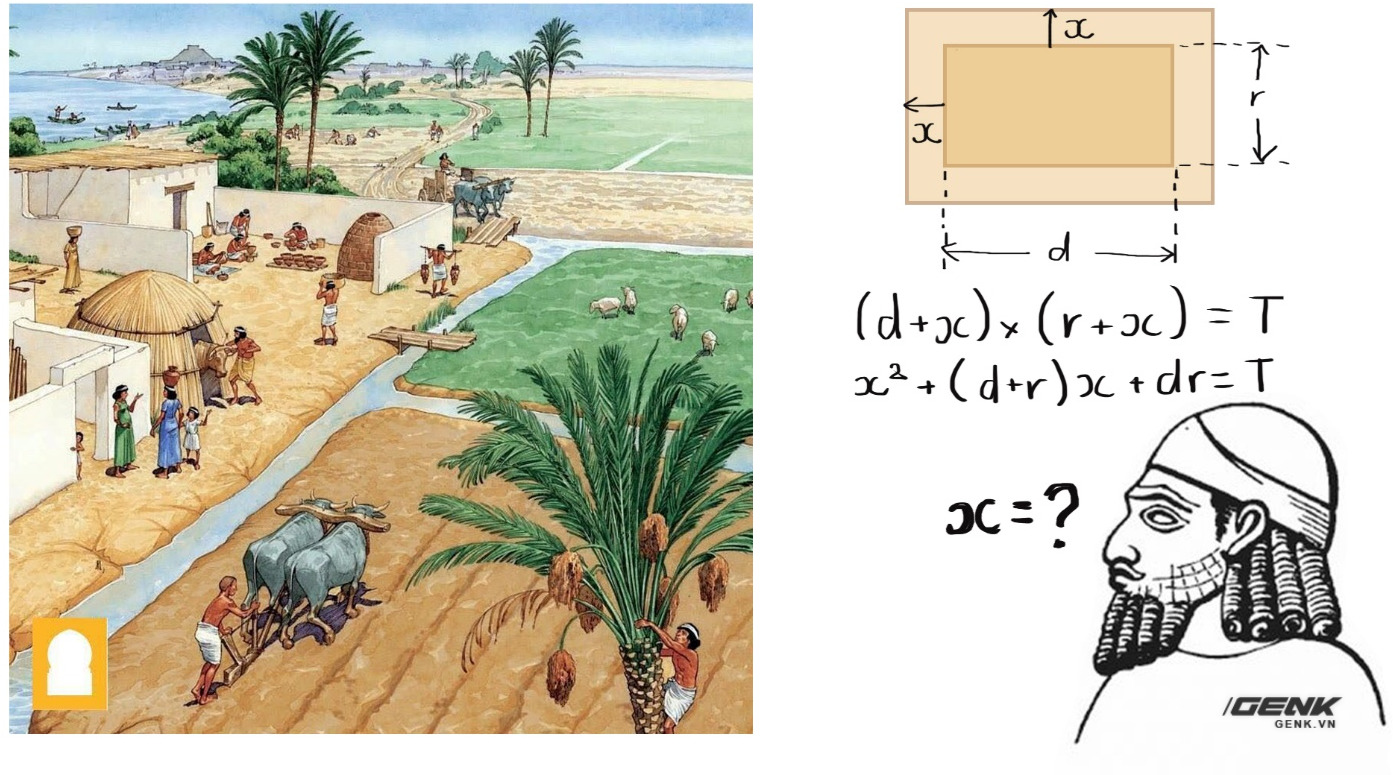
Xuyên suốt lịch sử, những bài toán đòi hỏi con người phải giải phương trình bậc hai đã xuất hiện ở mọi nền văn minh, từ Babylon, Ai Cập, Ấn Độ cho tới Trung Quốc. Trong quá khứ, phương trình bậc hai đã được sử dụng để tính toán những diện tích khổng lồ – biểu tượng của văn minh, từ những bậc thang của kim tự tháp cho tới những mái ngói đền thờ, lăng tẩm.
Nhờ những ứng dụng từ cơ bản tới vĩ đại, phương trình bậc hai thời nay được đưa vào mọi chương trình toán học đại trà phổ thông trên quốc tế. Thật đáng tiếc, cách nó được dạy khá máy móc. Tất cả những giáo trình toán trung học đều bắt học viên thuộc lòng một công thức tính nghiệm của phương trình bậc hai tổng quát :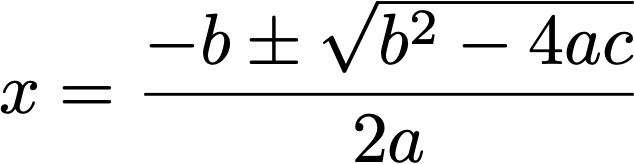
Đây thực sự rất khó nhớ và không mang tính trực quan chút nào. Giải phương trình bậc hai sử dụng công thức nghiệm gần như là một bài tập trí nhớ, thay vì rèn luyện suy luận. Nếu bạn hoàn toàn có thể nhớ công thức nghiệm, về cơ bản bạn sẽ giải được tổng thể những phương trình bậc hai. Chỉ có điều, toán học không sử dụng suy luận thật nhạt nhẽo và không có ý nghĩa .Đó là nguyên do mà Po-Shen Loh, một nhà toán học tại Đại học Carnegi Mellon, huấn luyện viên đội tuyển toán Olympic Hoa Kỳ muốn tìm ra một lời giải đơn thuần, trực quan và mang tính suy luận hơn cho phương trình bậc hai. Và anh ấy đã thành công xuất sắc .
Po-Shen Loh, huấn luyện viên đội tuyển toán Olympic Hoa KỳNăm 2019, Po-Shen Loh xuất bản một bài báo khoa học san sẻ về chiêu thức giải phương trình bậc hai mới của anh. Nó trọn vẹn vượt ra khỏi sự gò bó của việc vận dụng công thức nghiệm, không nhu yếu học viên phải nhớ công thức một cách máy móc, mà vẫn hoàn toàn có thể giải được mọi phương trình bậc hai, thậm chí còn với cả nghiệm phức .Hãy cùng tìm hiểu và khám phá đâu là cách Po-Shen Loh đã sử dụng :
1. Giả sử, ta có phương trình bậc hai như sau: x2 Bx C = 0
2. Với một chút quan sát hoặc nhớ lại định lý Viete, ta có thể thấy mọi đa thức vế trái đều có thể phân tích thành dạng:
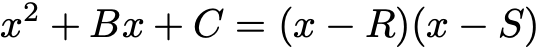
Nếu vế trái bằng 0, phương trình này sẽ có nghiệm x =R hoặc x = S. Cơ bản, đó chính là hai nghiệm của phương trình bậc hai đã cho.
Bây giờ, khi nhân bung vế phải để phá ngoặc, ta sẽ có :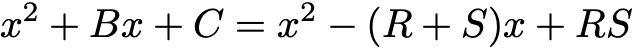
Phương trình này tương đương với -B = R S và C = R.S. Không có gì đặc biệt, nó chỉ giống với những gì mà nhà toán học người Pháp Viete đã rút ra được từ thế kỷ 16. Nhưng bước sau này là sự sáng tạo của Po-Shen Loh, khi anh đã dùng cùng một cách mà các nhà toán học thời Babylon cổ đại đã dùng để giải tiếp phương trình.
3. Po-Shen Loh nhận thấy nếu -B là tổng của R và S, thì trung bình cộng của R và S sẽ là -B/2. Ta gọi z là giá trị tuyệt đối của hiệu số giữa R và S với số trung bình cộng. Khi đó, ta có thể biểu diễn R và S theo -B/2 và chỉ còn duy nhất z là đại lượng chưa biết:
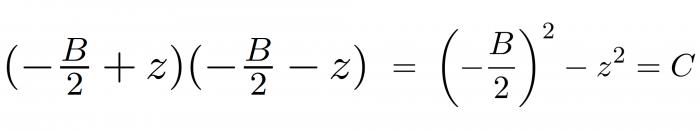
Sau đó, chúng ta đơn giản là chuyển vế rồi lấy căn bậc hai để tìm ra z:
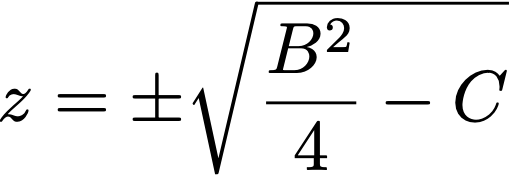
4. Lắp z trở lại R và S, ta sẽ được 2 nghiệm của phương trình ban đầu là:
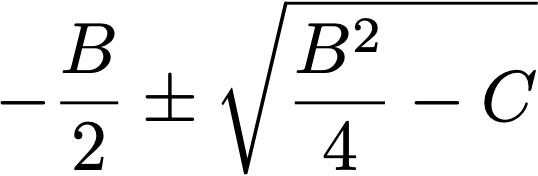
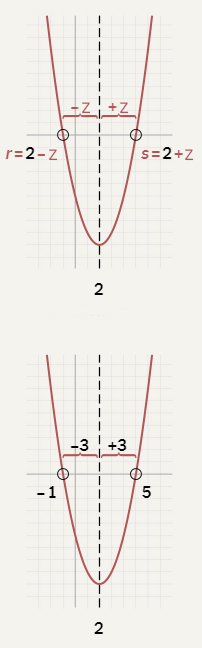TADA ! Nhìn thì có vẻ cũng có chút phức tạp. Nhưng hãy thử vận dụng vào một phương trình bậc hai để xem nó đơn thuần đến thế nào. Ta hoàn toàn có thể dùng đồ thị để tưởng tượng về chiêu thức của Po-Shen Loh :
Giả sử ta có hàm số y = x2 – 4x -5. Hàm số này được thể hiện là một parabol trên đồ thị bên phải. Ở hai điểm giao của parabol với trục hoành, ta có x2 – 4x -5 =0, chính là một phương trình bậc hai. Hoành độ của 2 giao điểm chính là nghiệm của phương trình này: R và S.
Theo định lý Viete, R S = 4, trung bình cộng của R và S là 2.
z là nửa khoảng cách giữa R và S, là đại lượng chưa biết thì R =2-z và S = 2 z.
Áp dụng tiếp định lý Viete, ta có R.S = -5. Nghĩa là (2-z). (2 z)= -5.
Nhân phá ngoặc, ta được 4-z2=-5
Tương đương với z2=9, z=3.
Vậy nghiệm của phương trình đầu tiên là R =2-3= -1 và S = 2 3= 5.
Tiếp tục thử cách giải của Po-Shen Loh với một phương trình bậc hai khác có nghiệm phức, ta thấy nó vẫn đúng. Giả sử phương trình lúc này là: x2 -2x 4 = 0.
Khi đã quen với phương pháp của Po-Shen Loh, ta có thể nhẩm nhanh phương trình này sẽ có 2 nghiệm: -B/2 ± z. Ở đây, B =-2 nên ta có 2 nghiệm là 1 ± z. Vì tích hai nghiệm phải bằng C =4, ta lại có:
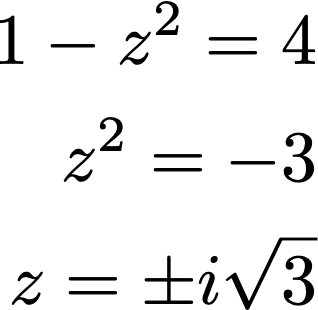Vậy, ở đầu cuối hai nghiệm của phương trình khởi đầu là :
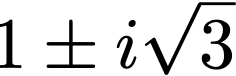Cùng một phương trình này, nếu giải bằng công thức nghiệm sẽ trở nên phức tạp hơn nhiều. Do đó, chiêu thức của Po-Shen Loh vừa đơn thuần, mang tính suy luận lại trực quan. Nó cũng hoàn toàn có thể vận dụng với mọi phương trình bậc hai mà bạn gặp .
Nếu phương trình có dạng Ax2 Bx C = 0, bạn chỉ việc chia tất cả các hệ số cho A để được phương trình mới dạng x2 (B/A) x C/A = 0 và áp dụng cách giải của Po-Shen Loh như bình thường.
Một chiêu thức phát minh sáng tạo hơn khi giải phương trình bậc haiNăm 2019, ngay khi bài báo khoa học của Po-Shen Loh được phát hành trên arXiv. org, một loạt những giáo viên toán đã phải kinh ngạc về giải thuật này. Điều mê hoặc là khi giải thuật của Po-Shen Loh được trình làng cho học viên, tổng thể đều hoàn toàn có thể thuận tiện vận dụng nó với sự thú vị hơn hẳn so với công thức nghiệm .Câu hỏi là tại sao từ trước đến nay chưa có ai vô tình tìm ra giải pháp này và san sẻ nó thoáng đãng ? Trên thực tiễn, Po-Shen Loh thừa nhận cách giải của mình chỉ là sự tích hợp giữa định lý Viete với một giải pháp của người Babylon có từ hàng ngàn năm trước .Tuy nhiên, anh cho biết từ trước đến nay chưa có ai từng phối hợp hai giải thuật này lại với nhau, để dạy cho học viên một cách tư duy đơn thuần nhưng rất là logic khi đi tìm nghiệm của phương trình bậc hai .Trong bài báo, Po-Shen Loh cho biết mình đã tìm lại toàn bộ những tài liệu ghi lại chiêu thức giải phương trình bậc hai của người Babylon cổ đại, Trung Quốc, Hy Lạp, Ấn Độ và Ả Rập cũng như những nhà toán học văn minh từ thời Phục hưng cho đến thời nay .Kết quả cho thấy không ai trong số họ từng giải phương trình bậc hai theo cách của anh, mặc dầu định lý Viete và những khai triển của người Babylon đã sống sót cách đây hàng trăm, hàng ngàn năm. Vâỵ thì tại sao giờ đây giải pháp này mới được phát hiện ?
Po-Shen Loh cho biết có thể đó là do cách tiếp cận của chúng ta với phương trình bậc hai. Các cách giải hiện đại, điển hình là dùng công thức nghiệm có thể chứng minh một phương trình bậc hai có nghiệm hay vô nghiệm. Nó khiến tính chất nghiệm bị bỏ qua một bên, chúng ta không mấy khi để ý rằng tổng hai nghiệm của phương trình bậc hai nếu có sẽ bằng -B còn tích của chúng bằng đúng hệ số C.
Ngoài ra, phương trình bậc hai giờ đây cũng chỉ gắn liền với những bài tập trong sách giáo khoa. Học sinh sẽ được dạy đi dạy lại những công thức, cách vận dụng chúng một cách máy móc .Không giống với trong quá khứ, người Babylon sử dụng phương trình bậc hai vào những bài toán thực tiễn mà họ gặp phải trong đời sống. Giải phương trình khi đó nhằm mục đích tìm ra đáp án, hay giải pháp cho yếu tố họ đang gặp phải .Vì thế, việc tìm ra nghiệm mới được chú trọng, và để làm được điều đó, tổ tiên của tất cả chúng ta trong quá khứ đã có nhiều chiêu thức phát minh sáng tạo hơn .
Po-Shen Loh nghĩ toán học hoàn toàn có thể mê hoặc học viên hơn, nếu nó trực quan và trở nên đơn thuần .Bây giờ, sau khi phát hiện ra cách giải mới cho phương trình bậc hai, Po-Shen Loh đã ứng dụng nó vào ngay trong những chương trình giảng dạy của mình. Anh hiện vẫn đang là một nhà nghiên cứu toán học, một huấn luyện viên cho đội tuyển Olympic toán Hoa Kỳ .Nhưng điều tuyệt vời nhất so với Po-Shen Loh có lẽ rằng là sự tiếp đón rất hào hứng của những học viên với cách giải mới này. Nhiều học viên cho biết giải pháp giải này rất có ích. Với nó, họ đã hoàn toàn có thể tưởng tượng về phương trình bậc hai một cách trực quan hơn, chứ không còn là những số lượng và công thức khô khan nữa .
Po-Shen Loh cho biết cách giải này cũng nhấn mạnh một triết lý trong phương pháp giảng dạy của anh. “Tôi nghĩ nếu mình hay ai đó có thể làm cho toán học trở nên sống động trở lại, làm sao để mọi người bất kể ai cũng có thể hiểu và hấp thụ nó, thì lợi ích từ việc làm này sẽ rất lớn”.
Một khi học viên thấy toán học mê hoặc và hiểu được nó, họ sẽ không còn tâm ý sợ toán hay ngại toán nữa. Những người trước đây từng nghĩ rằng mình dốt toán hay đó không phải môn học dành cho mình cũng sẽ tự tin hơn khi đương đầu với môn học này .Rốt cuộc, toán học sau hàng ngàn năm vẫn rất sôi động và mê hoặc. Chỉ là cách tất cả chúng ta đang dạy và học toán đã biến nó thành một môn học khô khan và áp lực đè nén mà thôi .
Tham khảo MIT, Nytimes
Source: http://wp.ftn61.com
Category: Hỏi Đáp
Để lại một bình luận