Cách giải phương trình bằng phương pháp biến đổi tương đương cực hay
Trang trước Trang sau Quảng cáo- Phương trình tương đương : Hai phương trình f1 ( x ) = g1 ( x ) và f2 ( x ) = g2 ( x ) được gọi là tương đương nếu chúng có cùng tập nghiệm- Kí hiệu là f1 ( x ) = g1 ( x ) f2 ( x ) = g2 ( x )
– Phép biến đổi không làm thay đổi tập nghiệm của phương trình gọi là phép biến đổi tương đương.
Bạn đang đọc: Phương trình tương đương là gì lớp 10
– Phương trình hệ quả : f2 ( x ) = g2 ( x ) gọi là phương trình hệ quả của phương trình f1 ( x ) = g1 ( x ) nếu tập nghiệm của nó chứa tập nghiệm của phương trình f1 ( x ) = g1 ( x )- Kí hiệu là f1 ( x ) = g1 ( x ) f2 ( x ) = g2 ( x )- Để giải phương trình ta triển khai những phép biến hóa để đưa về phương trình tương đương với phương trình đã cho đơn thuần hơn trong việc giải nó. Một số phép đổi khác thường sử dụng :+ Cộng ( trừ ) cả hai vế của phương trình mà không làm đổi khác điều kiện kèm theo xác lập của phương trình ta thu được phương trình tương đương phương trình đã cho .+ Nhân ( chia ) vào hai vế với một biểu thức khác không và không làm đổi khác điều kiện kèm theo xác lập của phương trình ta thu được phương trình tương đương với phương trình đã cho .+ Bình phương hai vế của phương trình ta thu được phương trình hệ quả của phương trình đã cho .Bình phương hai vế của phương trình ( hai vế luôn cùng dấu ) ta thu được phương trình tương đương với phương trình đã cho .
Bài 1: Giải phương trình
Hướng dẫn:
Điều kiện :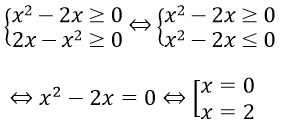
Bài 2: Giải phương trình
Hướng dẫn:
Điều kiện :Ta thấy x = 3 thỏa mãn nhu cầu điều kiện kèm theo ( * )Nếu x 3. thì ( * )
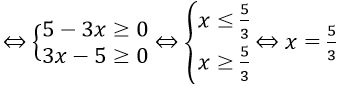
Bài 3: Giải phương trình
Hướng dẫn:
a. Điều kiện : x – 1 .Ta có x = – 1 là một nghiệm .Nếu x > – 1 thì ( x + 1 ) > 0. Do đó phương trình tương đương
x2 – x – 2 = 0 x = – 1 hoặc x = 2 .Đối chiếu điều kiện kèm theo ta được nghiệm của phương trình là x = – 1, x = 2 .Vậy phương trình đã cho có hai nghiệm S = { – 1 ; 2 }b. ĐKXĐ : x > 2Với điều kiện kèm theo đó phương trình tương đương với phương trìnhx2 = 1 – ( x – 2 ) x2 + x – 3 = 0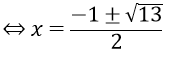
Bài 4: Giải phương trình
Hướng dẫn:
a. Điều kiện : x 1 .Với điều kiện kèm theo trên phương trình tương đương x2 – x + 1 = 2 x – 1 x = 1 hoặc x = 2Đối chiếu điều kiện kèm theo ta được phương trình có nghiệm duy nhất x = 2 .b. ĐKXĐ :Với điều kiện kèm theo đó phương trình tương đương với
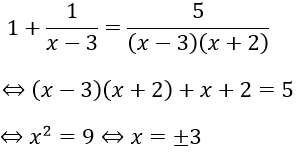
Bài 5: Tìm m để cặp phương trình sau tương đương
x2 + mx – 1 = 0 ( 1 ) và ( m-1 ) x2 + 2 ( m-2 ) x + m – 3 = 0 ( 2 )
Hướng dẫn:
Giả sử hai phương trình ( 1 ) và ( 2 ) tương đươngTa có ( m-1 ) x2 + 2 ( m-2 ) x + m – 3 = 0Do hai phương trình tương đương nên x = – 1 cũng là nghiệm của phương trình ( 1 )Thay x = – 1 vào phương trình ( 1 ) ta được m = 0Với m = 0 thay vào hai phương trình ta thấy không tương đương .
Vậy không có giá trị nào của m thỏa mãn.
Chuyên đề Toán 10 : rất đầy đủ triết lý và những dạng bài tập có đáp án khác :
Giới thiệu kênh Youtube Tôi
Trang trước Trang sau
Source: http://wp.ftn61.com
Category: Hỏi Đáp
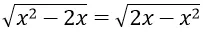
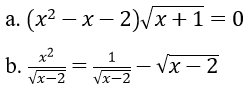
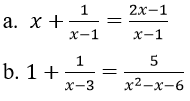


Để lại một bình luận