Các Dạng Toán Phương Trình Có Dạng A B C=0, Cách Nhẩm Nghiệm Phương Trình Bậc Hai

Cần phải có phương pháp giải và tính nhẩm nghiệm phương trình bậc 2 thật chính xác để làm bước khởi đầu tiến sâu vào tam thức bậc 2 và các bài toán liên quan khác.
Đang xem : Phương trình có dạng a b c = 0

Phương pháp giải và tính nhẩm nghiệm phương trình bậc 2
Nếu trong quy trình học tập, học viên vẫn chưa hiểu rõ về cách giải phương trình bậc 2, hãy cùng chúng tôi tìm hiểu thêm và tìm hiểu và khám phá cách giải cụ thể và cách tính nhẩm nghiệm phương trình bậc 2 trong bài viết san sẻ dưới đây nhé !

Phương trình bậc 2 là gì?

Phương trình bậc hai là phương trình có dạng: ax2 + bx + c = 0. Với

x là ẩn sốa, b, c là những số đã biết sao cho : a ≠ 0 a, b, c là những thông số của phương trình và hoàn toàn có thể phân biệt bằng cách gọi tương ứng với thông số của x ( theo phương trình trên thì a là thông số bậc hai, b là thông số bậc một, c là hằng số hay số hạng tự do ) .

Phương pháp giải phương trình bậc 2

Giải phương trình bậc 2 : ax2 + bx + c = 0 theo biệt thức delta ( Δ )

Định lý Vi-ét

Công thức Vi-ét về quan hệ giữa những nghiệm của đa thức với những thông số của nó. Trong trường hợp phương trình bậc hai một ẩn, được phát biểu như sau :

Một số trường hợp đặc biệt

Nếu phương trình bậc 2 có :

Cách tính nhẩm nghiệm phương trình bậc 2

Cách tính nhẩm nghiệm phương trình bậc 2

Giảng viên Trường Trung học đại trà phổ thông TP HCM san sẻ : Xuất phát từ định lý Vi-ét, tất cả chúng ta có những dạng toán tính nhẩm như sau :

Dạng 1: A = 1, B = Tổng, C = Tích

Nếu phương trình có dạng x2 – ( u + v ) x + uv = 0 thì phương trình đó có hai nhiệm u và v .
Nếu phương trình có dạng x2 + ( u + v ) x + uv = 0 thì phương trình có hai nghiệm – u và – v .

Tóm lại:

x2 – ( u + v ) x + uv = 0 => x1 = u, x2 = v ( 1 ) x2 + ( u + v ) x + uv = 0 => x1 = – u, x2 = – v
Như vậy, với dạng này tất cả chúng ta cần triển khai 2 phép nhẩm : “ Phân tích thông số c thành tích và b thành tổng ”. Trong hai phép nhẩm đó, tất cả chúng ta nên nhẩm thông số c trước rồi phối hợp với b để tìm ra hai số thỏa mãn nhu cầu tích bằng c và tổng bằng b .

Khi tiến hành, bạn nhẩm trong đầu như sau: Tích của hai nghiệm bằng c, mà tổng lại bằng b.

Xem thêm : Phương Trình Ion Rút Gọn Là Gì, Nghĩa Của Từ Phương Trình Ion Trong Tiếng Việt

Ví dụ phương trình:

x2 – 5 x + 6 = 0

Nhẩm: “Tích của hai nghiệm bằng 6, mà tổng lại bằng 5”. Hai số đó là: 2 và 3 vì 6 = 2×3 và 5 = 2 + 3. Vậy phương trình có hai nghiệm x = 2, x = 3.

x2 – 7 x + 10 = 0

Nhẩm: “Tích của hai nghiệm bằng 10, mà tổng lại bằng 7”. Hai số đó là: 2 và 5 vì 10 = 2×5 và 7 = 2 + 5. Vậy phương trình có hai nghiệm x = 2, x = 5.

Dạng 2: A + B + C = 0 và A – B + C = 0

x2 – ( u + v ) x + uv = 0 => x1 = u, x2 = v ( 1 )
Nếu thay v = 1 vào ( 1 ) thì tất cả chúng ta sẽ có trường hợp nhẩm nghiệm quen thuộc a + b + c = 0, với a = 1, b = – ( u + 1 ), c = u. Nếu thay v = – 1 vào ( 1 ) thì bạn sẽ có trường hợp nhẩm nghiệm a – b + c = 0, với a = 1, b = – ( u-1 ), c = – u .
Do loại này đã quá quen thuộc và thường gặp, nên bài viết không xét những ví dụ cho trường hợp này mà tập trung chuyên sâu vào Dạng 1 và Dạng 3 .

Dạng 3: Hai nghiệm là nghịch đảo của nhau

Nếu u ≠ 0 và v = 1 / u thì phương trình ( 1 ) có dạng :

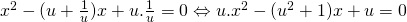
Khi đó : Phương trình có hai nghiệm là nghịch đảo của nhau x = u, x = 1 / u. Đây cũng là trường hợp hay gặp khi giải toán. Ví dụ phương trình :
2 × 2 – 5 x + 2 = 0 có hai nghiệm x = 2, x = 1/23 × 2 – 10 x + 3 = 0 có hai nghiệm x = 3, x = 1/3

Một số ví dụ vận dụng cách tính nhẩm nghiệm phương trình bậc 2

Một số ví dụ vận dụng

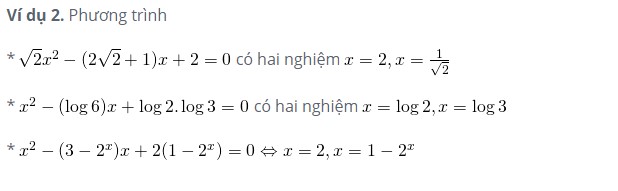
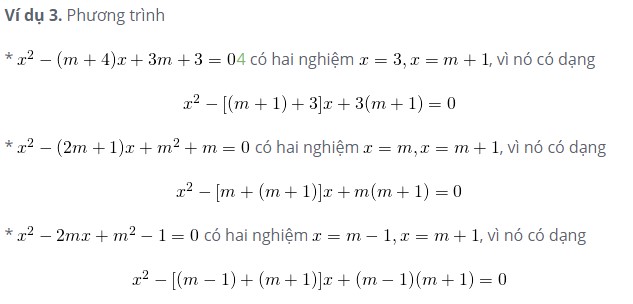
Dựa vào đó, các bạn hãy áp dụng và thử giải các bài tập sau đây nhé:

2×2 + 6x + 5 = 0x2 – 4x + 4 = 02×2 + 7x – 3 = 0.

Xem thêm : Cách Tính Tiền Chậm Nộp Tiền Thuê Đất, Cách Tính Tiền Sử Dụng Đất Chậm Nộp
Khi mới làm quen với tính nhẩm, hoàn toàn có thể tất cả chúng ta sẽ gặp một chút ít khó khăn vất vả, nhưng đừng cho nên vì thế mà ngại khó và bỏ cuộc. Hãy tưởng tượng thành quả mà giải pháp tính nhẩm đem lại cho tất cả chúng ta là “ không đếm được ” so với những “ trở ngại đếm được ” mà bạn đang phải đương đầu. Chúng ta sẽ có thêm động lực tiến lên .

Xem thêm bài viết thuộc chuyên mục: Phương trình

Điều hướng bài viết

Source: http://wp.ftn61.com
Category: Hỏi Đáp