Viết phương trình đường thẳng là giao tuyến của hai mặt phẳng
A. Phương pháp giải
Cách 1 :
+ Cả hai trường hợp đều suy ra 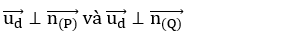
Mà ( P ) và ( Q. ) cắt nhau
=>Véc tơ chỉ phương của d là
+ Tìm một điểm M thuộc đường thẳng d .
+ Đường thẳng d đi qua M và nhận vecto làm vecto chỉ phương
=> phương trình tham số và phương trình chính tắc của đường thẳng
Cách 2 :
Nếu d là giao tuyến của hai mặt phẳng cắt nhau ( P ) và ( Q. ) thì với mỗi điểm
M ( x ; y ; z ) thuộc d là nghiệm của hệ phương trình :
Đặt x = t ( hoặc y = t hoặc z = t ) thay vào hệ ( * ) rồi rút y ; z theo t
Từ đó suy ra phương trình của đường thẳng d .

B. Ví dụ minh họa
Ví dụ 1: Trong không gian với hệ tọa độ Oxyz; gọi d là giao tuyến của hai mặt phẳng (α):x-3y+z=0 và (α’):x+y-z+4=0. Viết phương trình tham số của đường thẳng d
A.
B.
C.
D.
Hướng dẫn giải
* Cách 1 : Điểm M ( x ; y ; z ) ∈ d khi tọa độ của M là nghiệm của hệ phương trình :
Đặt y = t, ta có:
Vậy phương trình tham số của d là :
Cách 2 : Ta tìm một điểm thuộc đường thẳng d bằng cách cho y = 0 trong hệ ( * )
Ta có hệ
Vậy điểm M0 ( – 2 ; 0 ; 2 ) thuộc đường thẳng d .
Vectơ chỉ phương của đường thẳng d là
Chọn 1 vectơ chỉ phương của đường thẳng d là
Vậy phương trình tham số của d là :
Chọn C .
Ví dụ 2: Trong không gian với hệ tọa độ Oxyz; gọi d là giao tuyến của mặt phẳng (P): y – 2z + 3 = 0 và mặt phẳng tọa độ (Oyz).
A.
B.
C.
D.
Hướng dẫn giải
Mặt phẳng ( Oyz ) có phương trình x = 0
Điểm M ( x ; y ; z ) ∈ d khi tọa độ của M là nghiệm của hệ phương trình :
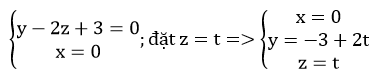
Chọn A .
Ví dụ 3: Viết phương trình đường thẳng d đi qua A (1; 2; – 1) và song song với đường thẳng giao tuyến của hai mặt phẳng (α):x+y-z+3=0 và (α’):2x-y+5z-4=0
A.
B.
C.
D.
Hướng dẫn giải
Vecto pháp tuyến của hai mặt phẳng là:
Vectơ chỉ phương của đường thẳng d là
Vậy phương trình đường thẳng d là
Chọn C .
Ví dụ 4: Viết phương trình đường thẳng d là giao tuyến của hai mặt phẳng (α):2x+y+1=0 và (β):x-y+z-1=0
A.
B.
C.
D. Đáp án khác
Hướng dẫn giải
Vecto pháp tuyến của hai mặt phẳng
Vectơ chỉ phương của đường thẳng d là
Điểm M ( x ; y ; z ) ∈ d khi đó tọa độ của M là nghiệm của hệ phương trình :
Ta tìm một điểm thuộc đường thẳng d bằng cách cho x = 0 trong hệ ( * )
Ta có hệ
Vậy điểm M0 ( 0 ; – 1 ; 0 ) thuộc đường thẳng d .
Vậy phương trình đường thẳng d là
Chọn C .
Ví dụ 5: Trong không gian với hệ tọa độ Oxyz; cho đường thẳng Δ là giao tuyến của hai mặt phẳng (α): x- 2y – z+10= 0 và (β): 2x+2y – 3z – 40= 0. Phương trình đường thẳng d đi qua điểm M(2; 3; 1) và song song với đường thẳng Δ là
A.
B.
C.
D.
giải
Mặt phẳng (α) có vec tơ pháp tuyến
Mặt phẳng (β ) có vec tơ pháp tuyến
Đường thẳng d đi qua điểm M và có vectơ chỉ phương là
Vậy phương trình của d là :
Chọn D .
Ví dụ 6: Trong không gian với hệ tọa độ Oxyz; cho hai mặt phẳng (P): x- 2y+ 2z- 9= 0 và (Q): 3x- 5y – 2z + 9= 0. Phương trình đường thẳng d đi qua điểm M(-2; -3; 5) và song song với hai mặt phẳng (P) và ( Q) là
A.
B.
C.
D.
Hướng dẫn giải
Mặt phẳng (P) có vectơ pháp tuyến
Mặt phẳng (Q) có vectơ pháp tuyến
Đường thẳng d đi qua điểm M ( – 2 ; – 3 ; 5 ) và có vectơ chỉ phương là :
Vậy phương trình của d là
Chọn A
Ví dụ 7: Trong không gian với hệ tọa độ (Oxyz) cho mặt phẳng (P): 2x- y+ 2z- 3= 0. Phương trình đường thẳng d đi qua điểm A(2; -3; -1 ), song song với hai mặt phẳng ( P) và ( Oyz) là.
A.
B.
C.
D.
Hướng dẫn giải
Mặt phẳng (P) có vectơ pháp tuyến
Mặt phẳng (Oyz) có phương trình x= 0 nên có vectơ pháp tuyến
Đường thẳng d đi qua điểm A ( 2 ; – 3 ; – 1 ) và có vectơ chỉ phương là
Vậy phương trình của d là
Chọn B .
Ví dụ 8. Trong không gian với hệ trục oxyz; cho đường thẳng d đi qua A(1; 0; -3) và song song với hai mặt phẳng ( Oxy) và ( Oxz). Viết phương trình của đường thẳng d?
A.
B.
C.
D.
Hướng dẫn giải
Mặt phẳng (Oxy) có phương trình z= 0 nên có vectơ pháp tuyến
Mặt phẳng (Oxz) có phương trình y= 0 nên có vectơ pháp tuyến
Xem thêm: Bộ Kế hoạch Đầu tư Tiếng Anh là gì?
Đường thẳng d đi qua điểm A(1;0;-3) và có vectơ chỉ phương là
Vậy phương trình của d là :
Chọn A .
Source: http://wp.ftn61.com
Category: Hỏi Đáp
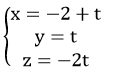
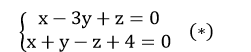
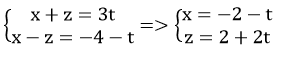
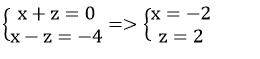
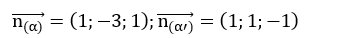
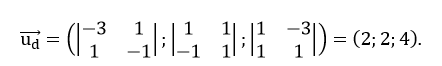
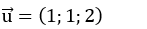
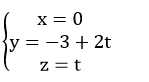
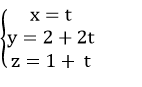
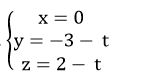
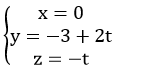
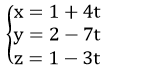
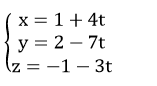
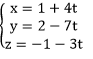
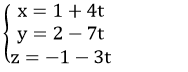
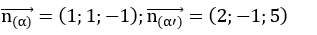
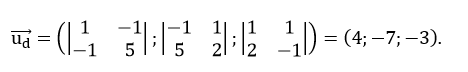
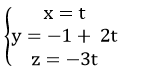
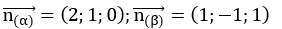
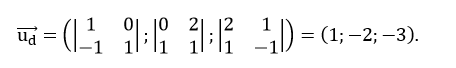
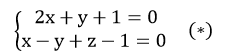
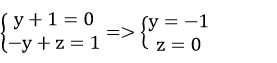
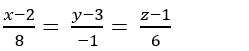
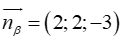
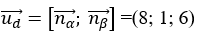
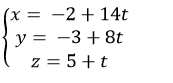
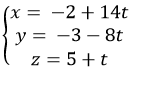
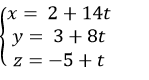
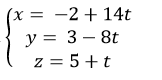
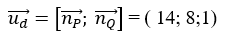
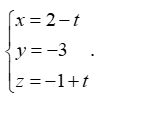
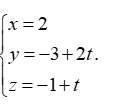
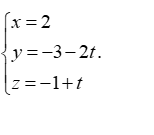
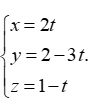
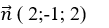
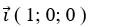
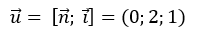
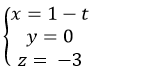
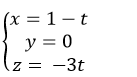
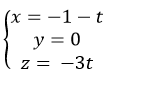
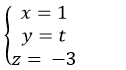


Để lại một bình luận