Giải đáp Toán học: Tổ hợp, chỉnh hợp, hoán vị là gì?

Tổ hợp chỉnh hợp, hoán vị đều là những khái niệm khá là mơ hồ so với những bạn học viên nên khi vận dụng vào những dạng bài tập thì hầu hết mọi người đều gặp phải những khó khăn vất vả. Đừng lo ngại, bài viết này sẽ giúp bạn biết công thức tổ hợp chỉnh hợp hoán vị là gì cũng như phân biệt được về hai khái niệm này .

Tổ hợp là gì?

Trong Toán học, tổ hợp là cách chọn những thành phần chứa từ một nhóm lớn hơn mà không phân biệt thứ tự .
Ví dụ : Có ba loại quả đó là một quả táo, một quả cam và một quả lê. Từ đây ta sẽ có ba cách để tích hợp hai loại quả từ tập hợp này như sau : một quả táo và một quả cam, một quả cam và một quả lê, một quả lê và một quả táo .

Theo định nghĩa, tổ hợp chập k của n phần tử chính là một tập hợp con của tập hợp mẹ S bao gồm n phần tử. Tập hợp con này sẽ gồm k phần tử riêng biệt thuộc S và không sắp thứ tự. Số tổ hợp chập k của n phần tử sẽ bằng với hệ số nhị thức.

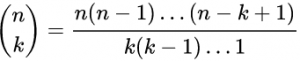
Công thức trên hoàn toàn có thể được viết dưới dạng giai thừa :

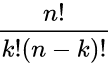
Trong đó :

k: trong số định nghĩa cần phải thỏa mãn điều kiện và kết quả sxe là 0 khi k > n. Tập hợp tất cả các tổ chập k của tập S thường được ký hiệu bởi .

Các tổ hợp hoàn toàn có thể là tổ chập gồm có k những thành phần khác nhau lấy từ n thành phần có sự tái diễn hoặc không lặp lại .

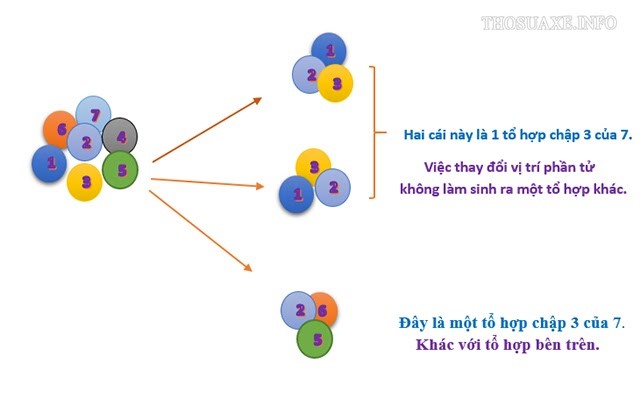
Chỉnh hợp là gì?

Trong Toán học thì chỉnh hợp là cách chọn những thành phần từ một nhóm nào đó lớn hơn và có phân biệt thứ tự. Nó khác với tổ hợp là không phân biệt thứ tự .
Theo khái niệm, chỉnh hợp chập k của n thành phần là một tập con của tập hợp mẹ S chứa n thành phần. Tập con này gồm k thành phần riêng không liên quan gì đến nhau thuộc S và có sắp xếp theo thứ tự .
Số chỉnh hợp chập k của một tập S thường được tính theo công thức sau :

Ví dụ : Với tập hợp E = { a, b, c, d }. Chỉnh hợp chập 3 của 4 thành phần trong E sẽ là :

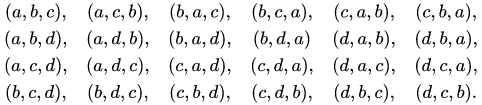
Số lượng chỉnh hợp mà bạn tính được sẽ là:

Trong Tiếng Việt, chỉnh hợp được ký hiệu bằng chữ A, đây là viết tắt của “Arrangement”.

Hoán vị là gì?

Trong Toán học đặc biệt quan trọng là trong đại số và những nghành có tương quan thì, một hoán vị sẽ là một tuy nhiên ánh từ một tập hợp hữu hạn X vào chính nó. Bên cạnh đó, theo triết lý tổ hợp thì hoán vị còn mang một ý nghĩa truyền thống cuội nguồn đó là miêu tả một bộ có thứ tự không lặp. Tuy nhiên, đến nay thì nó không còn được dùng nhiều nữa .
Cho tập hợp A gồm có n thành phần ( n ≥ 1 ). Mỗi hiệu quả của việc sắp xếp thứ tự n thành phần của tập hợp A sẽ được gọi là một hoán vị của n thành phần đó .
Công thức hoàn vị :

Ký hiệu hoán vị của n thành phần là : Pn .

Phân biệt tổ hợp chỉnh hợp

Để phân biệt tổ hợp và chỉnh hợp ta hoàn toàn có thể dựa vào định nghĩa của hai thuật ngữ này .

Đối với chỉnh hợp:

Trong n thành phần của tập hợp A ta sẽ lấy ra k thành phần. Trong k thành phần đã lấy ra này ta sắp xếp chúng theo một thứ tự và mỗi cách sắp xếp như vậy ta sẽ được một chỉnh hợp. Ví dụ ta lấy ra 3 số là 1, 2, 3 sau đó từ 3 số này ta lại sắp xếp thành những số có 3 chữ số. Như vậy ta sẽ có những số như sau : 123, 132, 312, 321, 213, 231. Qua đây bạn hoàn toàn có thể nhận thấy với việc đổi khác vị trí ra đã có được 6 số khác nhau và mỗi số đó lại là 1 chỉnh hợp .

Đối với tổ hợp

Tròn n thành phần của tập hợp A ta lấy ra một tập con gồm k thành phần. Khi nói đến khái niệm tổ hợp ta sẽ không phân biệt vị trí hay thứ tự của những thành phần trong đó, mà tất cả chúng ta chỉ chăm sóc xem trong tập đó có bao nhiêu thành phần thôi. Mỗi cách ta sẽ lấy ra một tập con gồm k thành phần cứu như vậy ta thu được một tổ hợp .
Ví dụ : Ta lấy ra 3 thành phần là những số : 1, 2, 3. Sau đó những số này ta sẽ đặt vào những vị trí khác nhau trong tập con. Từ đó, ta thu được những tập con là : A = { 1 ; 2 ; 3 } ; B = { 1 ; 2 ; 3 } ; C = { 2 ; 2 ; 3 } ; D = { 2 ; 3 ; 1 } ; E = { 3 ; 1 ; 2 } ; F = { 3 ; 2 ; 1 } .
Qua đây những bạn sẽ thấy tất cả chúng ta thu về được 6 tập con là A, B, C, D, E, F thế nhưng những thành phần vẫn là 1, 2, 3. Vậy nên 6 tập con ở trên là bằng nhau hay nói đơn thuần thì chúng là một .

Qua lý thuyết tổ hợp chỉnh hợp và hai ví dụ đưa ra để phân biệt tổ hợp chỉnh hợp trên đây bạn có thể thấy chỉnh hợp bao giờ cũng nhiều số hơn tổ hợp. Bởi vì chỉnh hợp còn phân biệt cả vị trí và thứ tự của các phần tử.

Các dạng bài tập của tổ hợp, chỉnh hợp, hoán vị

Các dạng bài tập phổ cập của tổ hợp, chỉnh hợp, hoán vị đó là :

• Dạng 1 là bài toán đếm

  Xem thêm: Làm Thế Nào Để Jailbreak Iphone?

• Dạng 2 là xếp vị trí – cách chọn và phân công việc làm
• Dạng 3 là đếm tổ hợp tương quan đến hình học .

Như vậy bài viết trên vừa chia sẻ cho bạn đọc các thông tin hữu ích liên quan đến tổ hợp chỉnh hợp và hoán vị. Hy vọng những kiến thức chia sẻ tại bài viết trên sẽ giúp ích được bạn đọc trong quá trình học tập.

Source: http://wp.ftn61.com
Category: Thủ Thuật