Trả lời câu hỏi Toán 10 Đại số Bài 1 trang 53: Nêu ví dụ về phương trình một ẩn, phương trình hai ẩn
Lời giải
Phương trình một ẩn: 2x + 4 = 0
Phương trình hai ẩn : 3 x + 7 y = 10
Trả lời câu hỏi Toán 10 Đại số Bài 1 trang 54: Cho phương trình
Khi x = 2 vế trái của phương trình đã cho có nghĩa không ? Vế phải có nghĩa khi nào ?
Lời giải
Khi x = 2 vế trái của phương trình đã cho không có nghĩa do mẫu bằng 0
Vế phải có nghĩ khi x – 1 ≥ 0 ⇔ x ≥ 1
Trả lời câu hỏi Toán 10 Đại số Bài 1 trang 54: Hãy tìm điều kiện của các phương trình
Lời giải
a ) ĐKXĐ : 2 – x > 0 ⇔ x < 2
Trả lời câu hỏi Toán 10 Đại số Bài 1 trang 55: Các phương trình sau có tập nghiệm bằng nhau hay không
a ) x2 + x = 0 và 4 x / ( x-3 ) + x = 0 ?
b ) x2 – 4 = 0 và 2 + x = 0 ?
Lời giải
a ) x2 + x = 0 ⇔ x ( x + 1 ) = 0 ⇔ x = 0 hoặc x = – 1
Tập nghiệm của phương trình là S = { 0 ; – 1 }
* 4 x / ( x-3 ) + x = 0 ĐKXĐ : x ≠ 3
⇒ 4 x + x ( x – 3 ) = 0
⇔ x2 + x = 0 ⇔ x ( x + 1 ) = 0 ⇔ x = 0 hoặc x = – 1
Tập nghiệm của phương trình là S = { 0 ; – 1 }
Vậy hai phương trình trên có cùng tập nghiệm .
b ) x2 – 4 = 0 ⇔ x = ± 2
Tập nghiệm của phương trình là S = { 2 ; – 2 }
* 2 + x = 0 ⇔ x = – 2
Tập nghiệm của phương trình là S = { – 2 }
Vậy hai phương trình trên không cùng tập nghiệm
Trả lời câu hỏi Toán 10 Đại số Bài 1 trang 56: Tìm sai lầm trong phép biến đổi sau
Lời giải
Phép biến hóa tiên phong không tương tự do biểu thức 1 / ( x-1 ) chưa có điều kiện kèm theo xác lập ( chỉ được dùng dấu suy ra trong phép biến hóa này )
Bài 1 (trang 57 SGK Đại số 10): Cho hai phương trình:
3 x = 2 và 2 x = 3
Cộng những vế tương ứng của hai phương trình đã cho. Hỏi :
a ) Phương trình nhận được có tương tự với một trong hai phương trình đã cho hay không ?
b ) Phương trình đã cho có phải là phương trình hệ quả của một trong hai phương trình đã cho hay không ?
Lời giải:
a ) Cộng những vế tương ứng của hai phương trình ta được :
5 x = 5 ⇔ x = 1
Trong khi :
3 x = 2 ⇔ x = 2/3
và 2 x = 3 ⇔ x = 3/2
Nên phương trình mới không tương tự với một trong hai phương trình đã cho .
b ) Phương trình này không phải là phương trình hệ quả của một trong hai phương trình. Bởi vì nghiệm của một trong hai phương trình đã cho không phải là nghiệm của phương trình mới .
Bài 2 (trang 57 SGK Đại số 10): Cho hai phương trình:
4 x = 5 và 3 x = 4
Nhân những vế tương ứng của hai phương trình đã cho. Hỏi :
a ) Phương trình nhận được có tương tự một trong hai phương trình đã cho hay không ?
b ) Phương trình đó có phải là phương trình hệ quả của một trong hai phương trình đã cho hay không ?
Lời giải:
Nhân các vế tương ứng của hai phương trình đã cho ta được phương trình:
a ) Phương trình nhận được không tương tự một trong hai phương trình đã cho vì chúng không có cùng tập nghiệm ( không tuân thủ theo phép biến hóa tương tự ) .
b ) Phương trình nhận được không là phương trình hệ quả của một trong hai phương trình đã cho vì nó không chưa tập nghiệm của một trong hai phương trình đã cho .
Bài 3 (trang 57 SGK Đại số 10): Giải các phương trình
Lời giải:
a ) Ta có :
Vậy phương trình có nghiệm duy nhất x = 1
b ) Điều kiện :
Giá trị x = 2 nghiệm đúng với phương trình nên phương trình có nghiệm duy nhất x = 2 .
c ) Ta có :
Vậy phương trình có nghiệm duy nhất x = 3
d ) Điều kiện :
Vậy phương trình đã cho vô nghiệm .
Bài 4 (trang 57 SGK Đại số 10): Giải các phương trình
Lời giải:
a ) Điều kiện : x ≠ 3
Ta có :
⇔ x + 1 = 1
⇔ x = 0 ( thỏa mãn nhu cầu điều kiện kèm theo )
Vậy phương trình có nghiệm x = 0 .
b ) Điều kiện : x ≠ 1
Ta có :
⇔ 2 x ( x – 1 ) + 3 = 3 x
⇔ 2×2 – 2 x + 3 = 3 x
⇔ 2×2 – 5 x + 3 = 0
⇔ ( x – 1 ) ( 2 x – 3 ) = 0
⇔ x1 = 1 ( loại ) ; x2 = 3/2 ( thỏa mãn nhu cầu )
Vậy phương trình có nghiệm x = 3/2 .
( Phương trình có a + b + c = 2 – 5 + 3 = 0 nên phương trình có 1 nghiệm : x1 = 1 )
c ) Điều kiện : x > 2
Ta có :
⇔ x2 – 4 x – 2 = x – 2
⇔ x2 – 5 x = 0
⇔ x ( x – 5 ) = 0
⇔ x = 0 ( loại )
x = 5 ( thỏa mãn nhu cầu điều kiện kèm theo )
Vậy phương trình có nghiệm x = 5 .
d )
⇔ 2×2 – x – 3 = 2 x – 3
⇔ 2×2 – 3 x = 0
⇔ x(2x – 3) = 0
⇔ x = 0 ( loại )
x = 3/2 ( loại )
Vậy phương trình đã cho vô nghiệm .
Post navigation
Source: http://wp.ftn61.com
Category: Hỏi Đáp
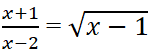
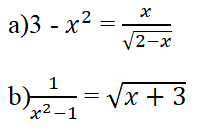
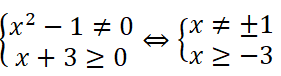

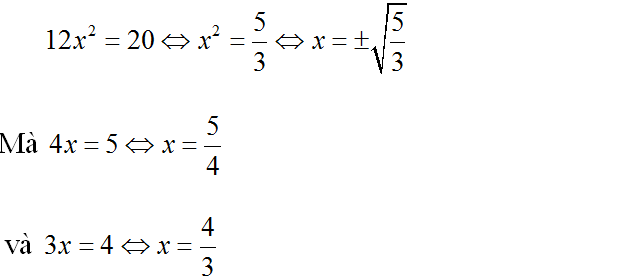

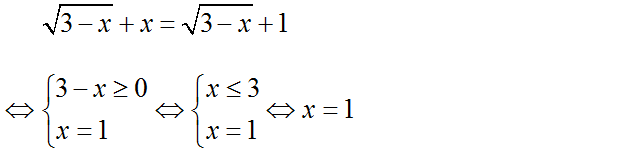
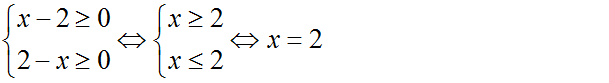
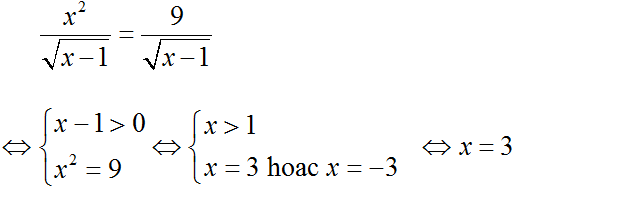
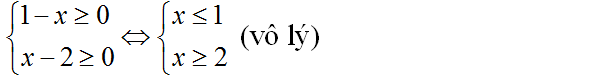
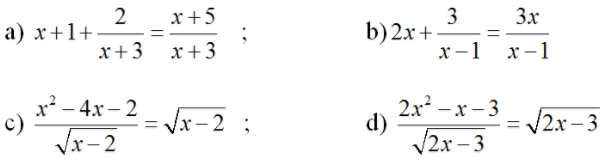
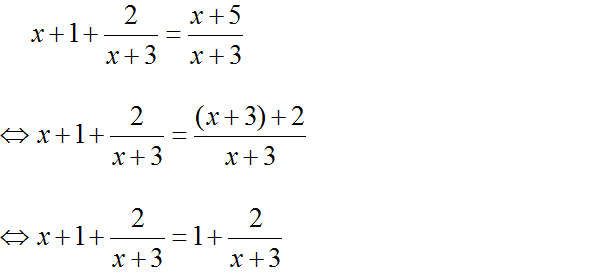
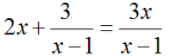
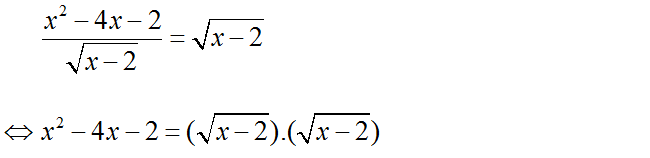
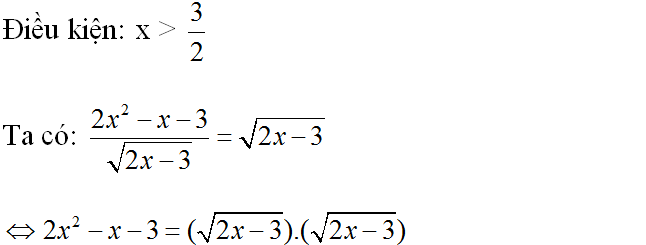



Để lại một bình luận