Viết Phương Trình Đường Thẳng Đi Qua 2 Điểm Cực Trị Cực Hay, Có Lời Giải

Trong những đề thi ĐH, một phần không hề thiếu là những bài toán về cực trị của hàm số. Một dạng toán thường hay gặp là tìm giá trị tham số để hàm số có cực trị và cực trị thỏa đặc thù P nào đó. Bài toán viết phương trình đường thẳng đi qua hai điểm cực trị của hàm số bậc ba đóng vai trò quan trọng và có nhiều dạng toán cần sử dụng đường thẳng đi qua hai điểm cực trị .
Đang xem : Viết phương trình đường thẳng đi qua 2 điểm cực trị
Trong một bài viết nhỏ này, tất cả chúng ta sẽ bàn về cách viết phương trình đường thẳng đi qua hai điểm cực trị của hàm số bậc ba ( nếu có ) và những ứng dụng của nó .

I – ĐIỀU KIỆN CẦN VÀ ĐỦ ĐỂ HÀM SỐ BẬC BA CÓ CỰC TRỊ

Xét hàm số

có

Hàm số có cực trị khi và chỉ khi phương trình

có hai nghiệm phân biệt và đổi dấu qua hai nghiệm đó .
Khi đó, nếu

là điểm cực trị thì giá trị cực trị
được tính như sau :

II – ĐƯỜNG THẲNG ĐI QUA HAI ĐIỂM CỰC TRỊ

1. Phương trình đường thẳng đi qua hai điểm cực trị

Giả sử hàm số bậc ba
có hai điểm cực trị là

. Khi đó, triển khai phép chia
cho

ta được :
Do đó, ta có :

Suy ra, những điểm
nằm trên đường thẳng

2. Áp dụng

a ) Có thể sử dụng phương trình đường thẳng đi qua cực lớn, cực tiểu để tìm cực trị khi biết điểm cực trị của hàm số .
b ) Vận dụng hệ thức Vi-et và phương trình đường thẳng đi qua cực lớn, cực tiểu để xử lý bài toán tìm giá trị tham số để hàm số có CĐ, CT thỏa đặc thù P .
Xem thêm : Tính Cách Con Gái Nghệ An, Anh Nhé, Người Nghệ Thấy Đúng Mới Phò

III- MỘT SỐ VÍ DỤ ÁP DỤNG

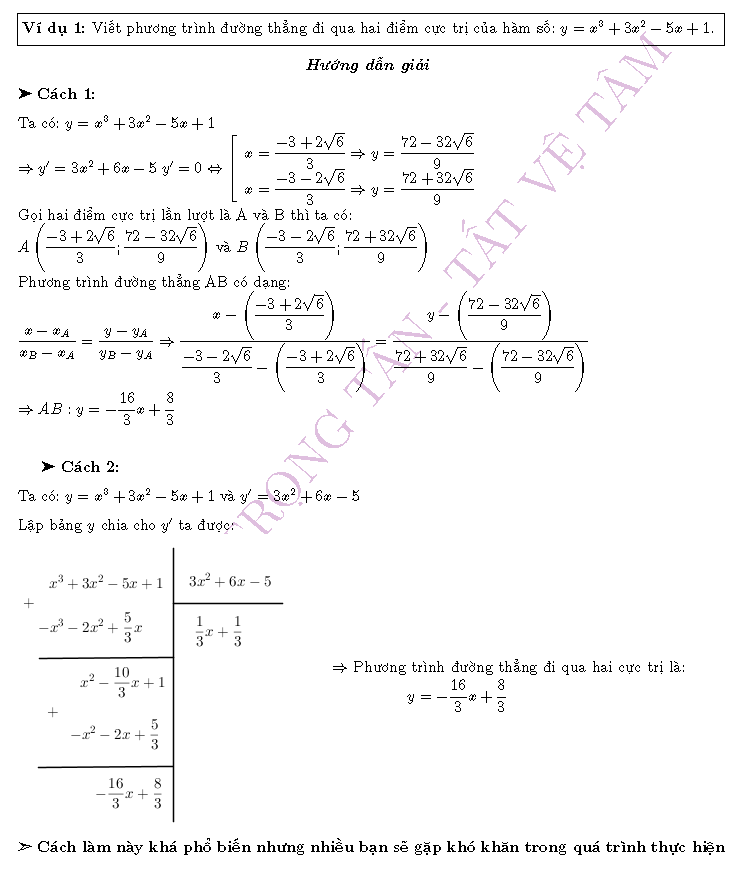
Ví dụ 1: Viết phương trình đường thẳng đi qua các điểm cực trị của hàm số sau

a )
b )

Giải:

a ) Ta có :
có hai nghiệm phân biệt. Thực hiện phép chia
cho
ta được

Đường thẳng đi qua hai điểm cực trị là
.
b ) Ta có

có hai nghiệm phân biệt nên hàm số có hai điểm cực trị. Đường thẳng đi qua hai điểm cực trị là :

Ví dụ 2: Cho hàm số

( m là tham số )
a ) Tìm

để hàm số có cực lớn cực tiểu .
b ) Với

như trên hãy viết phương trình đường thẳng đi qua các điểm cực trị của đồ thị hàm số.

Giải:

a ) Ta có :

0 ″ class = ” latex ” / >
Vậy hàm số luôn có cực lớn, cực tiểu với mọi
b ) Thực hiện phép chia y cho y ’, ta được :

Khi đó, đường thẳng đi qua hai điểm cực trị là :

Ví dụ 3: Cho hàm số

( 1 )
Tìm
để hàm số ( 1 ) có đường thẳng đi qua hai điểm cực trị song song với đường thẳng

Giải:

Ta có :
Hàm số có cực lớn, cực tiểu khi và chỉ khi
0 ″ class = ” latex ” / >

( 1 )
Thực hiện phép chia
cho
ta có phương trình đường thẳng đi qua cực lớn, cực tiểu là :

.
Xem thêm : Tính Cách Phù Hợp Với Nghề Nhân Sự, Những Phẩm Chất Cần Có Của Một Người Làm Nhân Sự
Để đường thẳng đi qua những điểm cực trị song song với đường thẳng
ta phải có :

Kết hợp với điều kiện kèm theo ( 1 ), ta có giá trị
cần tìm là :
;

Ví dụ 4: Cho hàm số

. Tìm
để đường thẳng đi qua cực lớn cực tiểu của đồ thị hàm số vuông góc với đường thẳng
.

Giải:

Ta có :

Hàm số có cực lớn, cực tiểu
0 \ Leftrightarrow \ left < \ begin { array } { l } m > \ sqrt { 21 } \ \ m
Thực hiện phép chia
cho
ta có phương trình đường thẳng đi qua cực lớn, cực tiểu là :

Để đường thẳng đi qua cực lớn, cực tiểu của hàm sô vuông góc với đường thẳng
, ta phải có :

Xem thêm bài viết thuộc chuyên mục: Phương trình

Điều hướng bài viết

Source: http://wp.ftn61.com
Category: Hỏi Đáp