Giải Toán 9 Bài 3: Giải hệ phương trình bằng phương pháp thế

Để quá trình tiếp thu kiến thức mới trở nên dễ dàng và đạt hiệu quả nhất, trước khi bắt đầu bài học mới các em cần có sự chuẩn bị nhất định qua việc tổng hợp nội dung kiến thức lý thuyết trọng tâm, sử dụng những kiến thức hiện có thử áp dụng giải các bài toán, trả lời câu hỏi liên quan. Dưới đây chúng tôi đã soạn sẵn Lời giải Bài 3: Giải hệ phương trình bằng phương pháp thế đầy đủ nhất, giúp các em tiết kiệm thời gian. Nội dung chi tiết được chia sẻ dưới đây.

Bài 3: Giải hệ phương trình bằng phương pháp thế

Câu hỏi ôn tập

Câu 1 trang 14:

Giải hệ phương trình sau bằng phương pháp thế ( màn biểu diễn y theo x từ phương trình thứ hai của hệ )

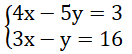
Hướng dẫn giải chi tiết:

Ta có ( màn biểu diễn y theo x từ phương trình thứ hai ) :

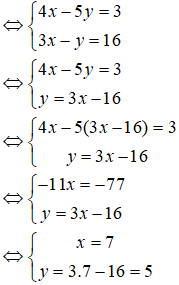
Vậy hệ phương trình có nghiệm duy nhất ( 7 ; 5 )

Câu 2 trang 15:

Bằng minh họa hình học, hãy lý giải tại sao hệ ( III ) có vô số nghiệm .

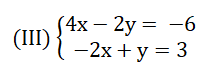
Hướng dẫn giải chi tiết:

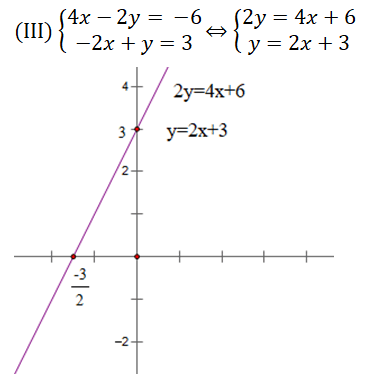
Hai đường thẳng trên trùng nhau nên hệ phương trình ( III ) có vô số nghiệm

Câu 3 trang 15:

Cho hệ phương trình

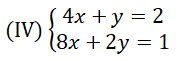
Bằng minh họa hình học và phương pháp thế, chứng tỏ rằng hệ ( IV ) vô nghiệm .

Hướng dẫn giải chi tiết:

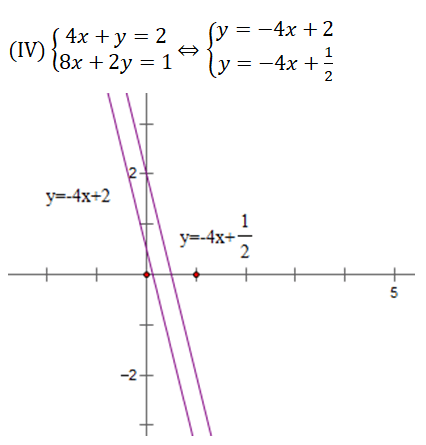
Hai đường thẳng trên song song nên chúng không có điểm chung hay hệ phương trình ( IV ) vô nghiệm .
Phương pháp thế :
Ta có ( trình diễn y theo x từ phương trình thứ nhất ) :

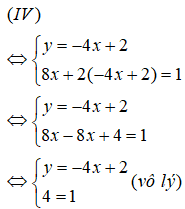
Vậy hệ phương trình ( IV ) vô nghiệm .

Bài tập:

Bài 12 (trang 15 SGK Toán 9 Tập 2): 

Giải những hệ phương trình sau bằng phương pháp thế :

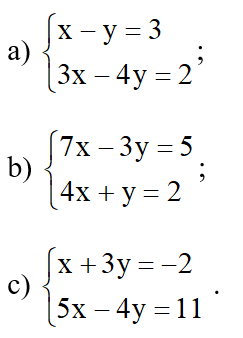
Hướng dẫn giải chi tiết:

Cách 1

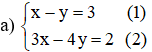
Từ ( 1 ) rút ra được y = x – 3
Thế vào phương trình ( 2 ) ta được :
3 x – 4. ( x – 3 ) = 2 ⇔ 3 x – 4 x + 12 = 2 ⇔ x = 10
Từ x = 10 ⇒ y = x – 3 = 7 .
Vậy hệ phương trình có nghiệm duy nhất ( 10 ; 7 ) .

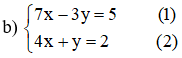
Từ ( 2 ) rút ra được y = – 4 x + 2 .
Thế y = – 4 x + 2 vào phương trình ( 1 ) ta được :

7x – 3.(-4x+2) = 5 ⇔ 7x + 12x – 6 = 5 ⇔ 19x = 11 ⇔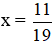 

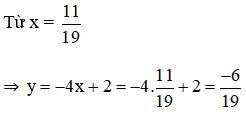
Vậy hệ phương trình có nghiệm duy nhất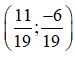 

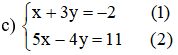
Từ ( 1 ) rút x theo y ta được : x = – 3 y – 2
Thế x = – 3 y – 2 vào phương trình ( 2 ) ta được :

5.(-3y – 2) – 4y = 11 ⇔ -15y – 10 – 4y = 11 ⇔ -19y = 21 ⇔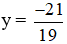 

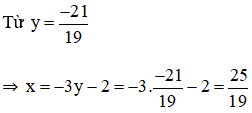
Vậy hệ phương trình có nghiệm duy nhất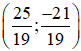 

Cách 2

  

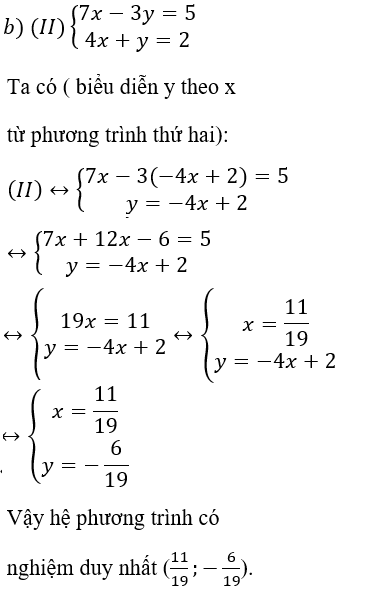
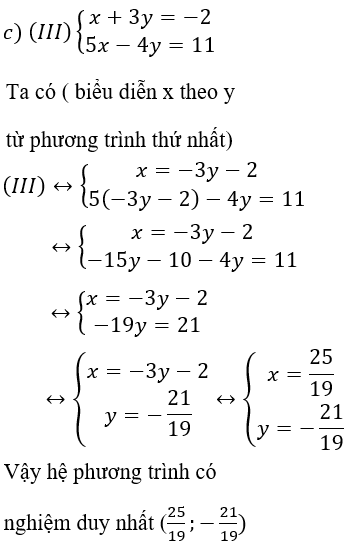
Kiến thức áp dụng

Giải hệ phương trình 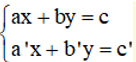 ta làm như sau:

Bước 1 : Từ một phương trình ( coi là phương trình thứ nhất ), ta màn biểu diễn x theo y ( hoặc y theo x ) ta được phương trình ( * ). Sau đó, ta thế ( * ) vào phương trình thứ hai để được một phương trình mới ( chỉ còn một ẩn ) ..
Bước 2 : Dùng phương trình mới ấy thay thế sửa chữa cho phương trình thứ hai, phương trình ( * ) thay thế sửa chữa cho phương trình thứ nhất của hệ ta được hệ phương trình mới tương tự ..
Bước 3 : Giải hệ phương trình mới ta tìm được nghiệm của hệ phương trình .

Bài 13 (trang 15 SGK Toán 9 Tập 2): 

Giải những hệ phương trình sau bằng phương pháp thế :

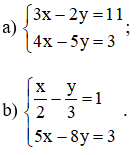
Hướng dẫn giải chi tiết:

Bài toán giải hệ phương trình bằng phương pháp thế có 2 cách trình diễn .

Cách 1:

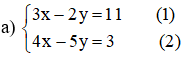
Từ (1) ta rút ra được  (*)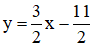

Thế ( * ) vào phương trình ( 2 ) ta được :

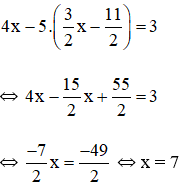
Thay x = 7 vào (*) ta suy ra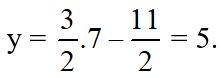 

Vậy hệ phương trình có nghiệm duy nhất ( 7 ; 5 ) .

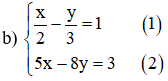
Từ (1) ta rút ra được :  (*)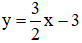

Thế ( * ) vào phương trình ( 2 ) ta được :

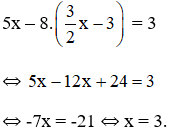
Thay x = 3 vào (*) ta suy ra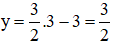 

Vậy hệ phương trình có nghiệm duy nhất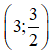 

Cách 2:

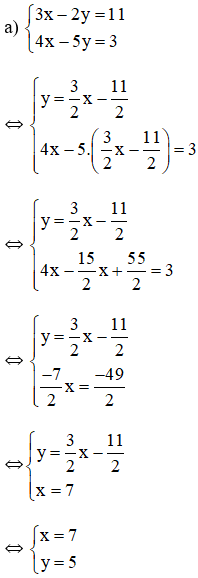
Vậy hệ phương trình có nghiệm duy nhất ( 7 ; 5 ) .

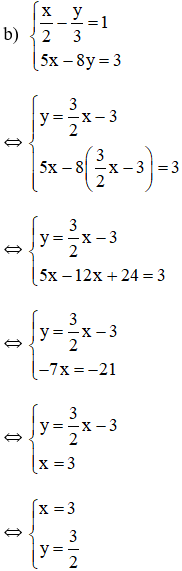
Vậy hệ phương trình có nghiệm duy nhất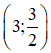 

Kiến thức áp dụng

Giải hệ phương trình ta làm như sau :
Bước 1 : Từ một phương trình ( coi là phương trình thứ nhất ), ta trình diễn x theo y ( hoặc y theo x ) ta được phương trình ( * ). Sau đó, ta thế ( * ) vào phương trình thứ hai để được một phương trình mới ( chỉ còn một ẩn ) .
Bước 2 : Dùng phương trình mới ấy thay thế sửa chữa cho phương trình thứ hai, phương trình ( * ) thay thế sửa chữa cho phương trình thứ nhất của hệ ta được hệ phương trình mới tương tự .
Bước 3 : Giải hệ phương trình mới ta tìm được nghiệm của hệ phương trình .

Bài 14 (trang 15 SGK Toán 9 Tập 2): 

Giải những hệ phương trình sau bằng phương pháp thế :

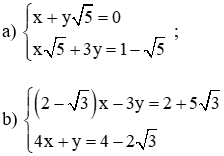
Hướng dẫn giải chi tiết:

Bài toán giải hệ phương trình bằng phương pháp thế có 2 cách trình diễn .

Cách 1:

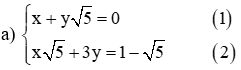
Từ ( 1 ) ta rút ra được x = – y √ 5 ( * )
Thế ( * ) vào phương trình ( 2 ) ta được :

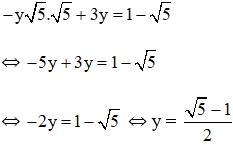
Thay 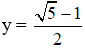 vào (*) ta được: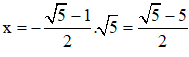 

Vậy hệ phương trình có nghiệm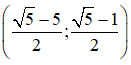 

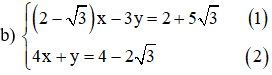
Từ ( 2 ) ta rút ra được y = – 4 x + 4 – 2 √ 3 ( * )
Thế ( * ) vào phương trình ( 1 ) ta được :

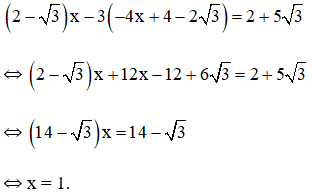
Thay x = 1 vào ( * ) ta được y = – 4.1 + 4 – 2 √ 3 = – 2 √ 3
Vậy hệ phương trình có nghiệm duy nhất ( 1 ; – 2 √ 3 )

Cách 2 :

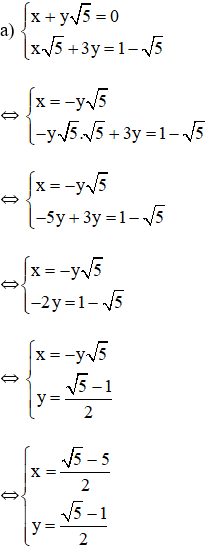
Vậy hệ phương trình có nghiệm duy nhất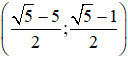 

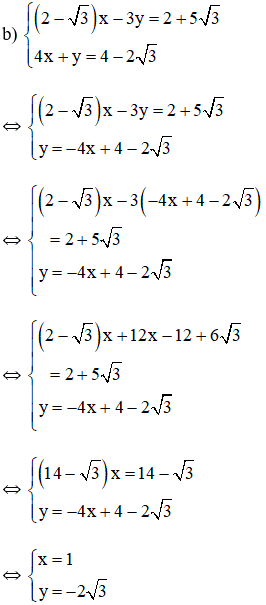
Vậy hệ phương trình có nghiệm duy nhất ( 1 ; – 2 √ 3 )

Kiến thức áp dụng

Giải hệ phương trình ta làm như sau :
Bước 1 : Từ một phương trình ( coi là phương trình thứ nhất ), ta màn biểu diễn x theo y ( hoặc y theo x ) ta được phương trình ( * ). Sau đó, ta thế ( * ) vào phương trình thứ hai để được một phương trình mới ( chỉ còn một ẩn ) .
Bước 2 : Dùng phương trình mới ấy sửa chữa thay thế cho phương trình thứ hai, phương trình ( * ) thay thế sửa chữa cho phương trình thứ nhất của hệ ta được hệ phương trình mới tương tự .
Bước 3 : Giải hệ phương trình mới ta tìm được nghiệm của hệ phương trình .

Còn tiếp:………

►Tải trọn bộ hướng dẫn giải bài tập chi tiết bài 3: Giải hệ phương trình bằng phương pháp thế tại đường link dưới đây:

Lý thuyết trọng tâm:

I. Quy tắc thế

Quy tắc thế dùng để biến hóa một hệ phương trình thành hệ phương trình tương tự. Quy tắc thế gồm hai bước sau :

    + Bước 1: Từ một phương trình của hệ đã cho (coi là phương trình thứ nhất), ta biểu diễn một ẩn theo ẩn kia rồi thế vào phương trình thứ hai để được một phương trình mới (chỉ còn một ẩn).

    + Bước 2: Dùng phương trình mới để thay thế cho phương trình thứ hai trong hệ (và giữ nguyên phương trình thứ nhất).

II. Tóm tắt cách giải hệ phương trình bằng phương pháp thế

Tóm tắt cách giải :

    + Bước 1: Dùng quy tắc thế biến đổi hệ phương trình đã cho để được một hệ phương trình mới, trong đó có một phương trình một ẩn.

    + Bước 2: Giải phương trình một ẩn vừa có, rồi suy ra nghiệm của hệ đã cho.

III. Chú ý khi giải hệ phương trình bằng phương pháp thế

Nếu thấy Open phương trình có những thông số của hai ẩn đều bằng 0 thì hệ phương trình đã cho hoàn toàn có thể có vô số nghiệm hoặc vô nghiệm .
Hy vọng tài liệu sẽ có ích cho những em học viên và quý thầy cô giáo tìm hiểu thêm và so sánh đáp án đúng chuẩn .
► Ngoài ra những em học viên và thầy cô hoàn toàn có thể tìm hiểu thêm thêm nhiều tài liệu có ích tương hỗ ôn luyện thi môn toán như đề kiểm tra học kì, 1 tiết, 15 phút trên lớp, hướng dẫn giải sách giáo khoa, sách bài tập được update liên tục tại chuyên trang của chúng tôi .

Source: http://wp.ftn61.com
Category: Hỏi Đáp