Để ôn luyện sâu kiến thức, các em cần tích cực giải các bài tập trong sách giáo khoa và sách bài tập từ đó tìm ra phương pháp giải hay cho các dạng toán, chuẩn bị tốt cho các kì thi sắp tới. Dưới đây là hướng dẫn giải bài tập Toán 8 Bài 7: Giải bài toán bằng cách lập phương trình (tiếp theo) từ đội ngũ chuyên gia giàu kinh nghiệm chia sẻ miễn phí, hỗ trợ các em ôn luyện hiệu quả. Mời các em học sinh cùng quý thầy cô tham khảo dưới đây.
Tóm tắt nội dung bài viết
Bài 7: Giải bài toán bằng cách lập phương trình (tiếp theo)
Trả lời câu hỏi Toán 8 Tập 2 Bài 7 trang 28:
Trong Ví dụ trên, hay thử chọn ẩn số theo cách khác : Gọi s ( km ) là quãng đường từ Thành Phố Hà Nội đến điểm gặp nhau của hai xe. Điền vào bảng sau rồi lập phương trình với ẩn số s :
| Vận tốc (km/h) | Quãng đường đi (km) | Thời gian đi (h) | |
| Xe máy | s | ||
| Ô tô |
Lời giải
| Vận tốc (km/h) | Quãng đường đi (km) | Thời gian đi (h) | |
| Xe máy | 35 | s | S/35 |
| Ô tô | 45 | 90 – s | (90 – S)/45 |
Ô tô xuất phát sau xe máy 2/5 giờ nên
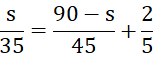
Trả lời câu hỏi Toán 8 Tập 2 Bài 7 trang 28:
Giải phương trình nhận được rồi suy ra đáp số của bài toán. So sánh hai cách chọn ẩn, em thấy cách nào cho giải thuật gọn hơn ?
Lời giải
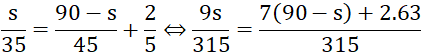
⇔ 9 s = 7 ( 90 – s ) + 126
⇔ 9 s = 756 – 7 s
⇔ 16 s = 756
⇔ s = 47,25 ( km )
Thời gian để hai xe gặp nhau từ lúc xe máy khởi hành là :
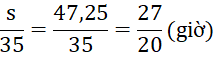
So sánh hai cách chọn ẩn, cách tiên phong ( chọn ẩn là thời hạn từ lúc xe máy khởi hành đến lúc hai xe gặp nhau ) cho cách giải ngắn gọn hơn vì phương trình đơn thuần hơn .
Bài 37 (trang 30 SGK Toán 8 tập 2):
Lúc 6 giờ sáng, một xe máy khởi hành từ A để đến B. Sau đó 1 giờ, một xe hơi cũng xuất phát từ A đến B với tốc độ trung bình lớn hơn tốc độ trung bình của xe máy 20 km / h. Cả hai xe đến B đồng thời vào lúc 9 giờ 30 phút sáng cùng ngày. Tính độ dài quãng đường AB và tốc độ trung bình của xe máy .
Lời giải:
* Phân tích bài toán:
Chọn x là tốc độ trung bình của xe máy .
( Các bạn hoàn toàn có thể chọn x là quãng đường AB và làm tựa như ) .
| Thời gian | Vận tốc | Quãng đường AB | |
| Xe máy | 3,5 | x | 3,5x |
| Ô tô | 2,5 | x + 20 | 2,5(x + 20). |
* Giải:
Gọi tốc độ trung bình của xe máy là x ( x > 0, km / h ) .
Thời gian xe máy đi từ A đến B : 9 h30 – 6 h = 3,5 ( h ) .
Quãng đường AB ( tính theo xe máy ) là : 3,5. x ( km ) .
Vận tốc trung bình của xe hơi lớn hơn tốc độ trung bình của xe máy 20 km / h
⇒ Vận tốc trung bình của xe hơi là : x + 20 ( km / h )
Ô tô xuất phát sau xe máy 1 h
⇒ thời hạn xe hơi đi từ A đến B là : 3,5 – 1 = 2,5 ( h ) .
Quãng đường AB ( tính theo xe hơi ) là : 2,5 ( x + 20 ) ( km )
Vì quãng đường AB là không đổi nên ta có phương trình :
3,5 x = 2,5 ( x + 20 ) ⇔ 3,5 x = 2,5 x + 50
⇔ 3,5 x – 2,5 x = 50 ⇔ x = 50 ( thỏa mãn nhu cầu ) .
⇒ Quãng đường AB : 3,5. 50 = 175 ( km ) .
Vậy quãng đường AB dài 175 km và tốc độ trung bình của xe máy là 50 km / h .
Kiến thức áp dụng
Các bước giải bài toán bằng cách lập phương trình :
Bước 1 : Lập phương trình
+ Chọn ẩn và đặt điều kiện kèm theo cho ẩn ( thường chọn đại lượng đề bài nhu yếu làm ẩn )
+ Biểu diễn toàn bộ các đại lượng khác qua ẩn vừa chọn .
+ Lập phương trình biểu lộ mối quan hệ giữa các đại lượng .
Bước 2 : Giải phương trình
Bước 3 : Đối chiếu điều kiện kèm theo rồi Kết luận .
Bài 38 (trang 30 SGK Toán 8 tập 2):
Điểm kiểm tra Toán của một tổ học tập được cho trong bảng sau :

Biết điểm trung bình của cả tổ là 6,6. Hãy điền các giá trị thích hợp vào hai ô còn trống ( được lưu lại * ) .
Lời giải:
Gọi x là số học sinh (tần số) được điểm 5 (x ∈ N; 0 ≤ x ≤ 4).
Tần số hay số học viên được điểm 9 là :
10 – ( 1 + 2 + 3 + x ) = 4 – x
Điểm trung bình của cả tổ bằng 6,6 điểm nên :

Kiến thức áp dụng
Các bước giải bài toán bằng cách lập phương trình :
Bước 1 : Lập phương trình
+ Chọn ẩn và đặt điều kiện kèm theo cho ẩn ( thường chọn đại lượng đề bài nhu yếu làm ẩn )
+ Biểu diễn toàn bộ các đại lượng khác qua ẩn vừa chọn .
+ Lập phương trình biểu lộ mối quan hệ giữa các đại lượng .
Bước 2 : Giải phương trình
Bước 3 : Đối chiếu điều kiện kèm theo rồi Kết luận .
Bài 39 (trang 30 SGK Toán 8 tập 2):
Lan mua hai loại hàng và phải trả tổng số 120 nghìn đồng, trong đó đã tính cả 10 nghìn đồng là thuế giá trị ngày càng tăng ( viết tắt là thuế Hóa Đơn đỏ VAT ). Biết rằng thuế Hóa Đơn đỏ VAT so với loại hàng thứ nhất là 10 % ; thuế Hóa Đơn đỏ VAT so với loại hàng thứ 2 là 8 %. Hỏi nếu không kể thuế Hóa Đơn đỏ VAT thì Lan phải trả mỗi loại hàng bao nhiêu tiền ?
Ghi chú : VAT là thuế mà người mua hàng phải trả, người bán hàng thu và nộp cho Nhà nước. Gỉa sử thuế Hóa Đơn đỏ VAT so với mẫu sản phẩm A được lao lý là 10 %. Khi đó nếu giá cả của A là a đồng thì kể cả thuế Hóa Đơn đỏ VAT, người mua loại sản phẩm này phải trả tổng số là a + 10 % a đồng .
Lời giải:
* Phân tích:
Vì trong 120000 Lan trả có 10000 thuế Hóa Đơn đỏ VAT nên giá gốc của hai mẫu sản phẩm không tính Hóa Đơn đỏ VAT là 110000 đồng .
| Giá gốc | Thuế VAT | |
| Hàng thứ 1 | x | 0,1.x |
| Hàng thứ 2 | 110000 – x | 0,08.(110000 – x) |
Thuế Hóa Đơn đỏ VAT của cả hai mẫu sản phẩm là 10 nghìn nên có phương trình :
0,1 x + 0,08 ( 110000 – x ) = 10000 .
* Giải
Gọi giá gốc của loại sản phẩm thứ nhất là x ( 0 < x < 110000 đồng ) . Vì trong 120000 đồng Lan trả đã có 10000 đồng thuế Hóa Đơn đỏ VAT nên tổng giá gốc của cả hai loại sản phẩm chỉ bằng : 120000 – 10000 = 110000 ( nghìn đồng ) . ⇒ Giá gốc của loại sản phẩm thứ hai là : 110000 – x ( đồng ) . Thuế Hóa Đơn đỏ VAT của loại sản phẩm thứ nhất bằng : 10 %. x = 0,1 x ( đồng ) . Thuế Hóa Đơn đỏ VAT của mẫu sản phẩm thứ hai bằng : 8 %. ( 110000 – x ) = 0,08. ( 110000 – x ) ( đồng ) . Thuế Hóa Đơn đỏ VAT của cả hai loại sản phẩm bằng : 0,1 x + 0,08 ( 110000 – x ) ( nghìn đồng ) . Theo đề bài, tổng thuế Hóa Đơn đỏ VAT của cả hai loại sản phẩm là 10000 đồng nên ta có phương trình : 0,1 x + 0,08 ( 110000 – x ) = 10000 ⇔ 0,1 x + 8800 – 0,08 x = 10000 ⇔ 0,02 x = 1200 ⇔ x = 60000 ( thỏa mãn nhu cầu điều kiện kèm theo ) . Vậy không kể Hóa Đơn đỏ VAT thì giá của mẫu sản phẩm thứ nhất là 60000 đồng, giá của loại sản phẩm thứ hai là 110000 – 60000 = 50000 đồng .
Kiến thức áp dụng
Các bước giải bài toán bằng cách lập phương trình :
Bước 1 : Lập phương trình
+ Chọn ẩn và đặt điều kiện kèm theo cho ẩn ( thường chọn đại lượng đề bài nhu yếu làm ẩn )
+ Biểu diễn tổng thể các đại lượng khác qua ẩn vừa chọn .
+ Lập phương trình biểu lộ mối quan hệ giữa các đại lượng .
Bước 2 : Giải phương trình
Bước 3 : Đối chiếu điều kiện kèm theo rồi Tóm lại .
►►Tải free hướng dẫn giải bài tập Toán 8 Bài 7: Giải bài toán bằng cách lập phương trình (tiếp theo) file word, pdf tại đường link dưới đây:
Hy vọng tài liệu sẽ có ích cho các em học viên và quý thầy cô giáo tìm hiểu thêm và so sánh đáp án đúng mực .
► Ngoài ra các em học viên và thầy cô hoàn toàn có thể tìm hiểu thêm thêm nhiều tài liệu có ích tương hỗ ôn luyện thi môn toán như đề kiểm tra học kì, 1 tiết, 15 phút trên lớp, hướng dẫn giải sách giáo khoa, sách bài tập được update liên tục tại chuyên trang của chúng tôi .
Source: http://wp.ftn61.com
Category: Hỏi Đáp



Để lại một bình luận