Tổng Hợp Các Dạng Phương Trình Lượng Giác Thường Gặp – VUIHOC

Trong chương trình toán trung học phổ thông, các em sẽ được làm quen với dạng bài về phương trình lượng giác thường gặp. Bài viết dưới đây Vuihoc. vn sẽ tổng hợp không thiếu về phương trình lượng giác thường gặp cùng ví dụ minh họa giúp các em hiểu bài nhanh hơn .

1. Phương trình bậc nhất đối với hàm số lượng giác sinx và cosx

Phương trình bậc nhất với một số ít hàm số lượng giác có dạng phương trình như sau :
at + b = 0

Trong đó:  a,b: hằng số (a≠0)

                  t: một trong các hàm số lượng giác

Phương trình lượng giác dạng asinx + bcosx = c, trong đó có a, b, c cùng thuộc R, USD a ^ { 2 } + b ^ { 2 } \ neq 0 $ là phương trình bậc nhất với sin ⁡ x và cos ⁡ x .
Ta xét :
+ Nếu USD a ^ { 2 } + b ^ { 2 } < c ^ { 2 } $ thì phương trình vô nghiệm . + Nếu USD a ^ { 2 } + b ^ { 2 } \ geqslant c ^ { 2 } $, để tìm nghiệm của phương trình ta triển khai tiếp các bước sau . Với phương trình bậc nhất so với hàm số lượng giác sinx và cosx, ta xét phương trình asinx + bcosx = c Lúc này : + Ta chia 2 vế của phương trình cho $ \ sqrt { a ^ { 2 } + b ^ { 2 } } $ + Gọi $ \ alpha USD là góc lượng giác được tạo ra bởi chiều dương của trục hoành với vectơ $ \ vec { OM } = ( a, b ) USD, phương trình trở thành : USD sin ( x + \ alpha ) = \ frac { c } { \ sqrt { a ^ { 2 } + b ^ { 2 } } } $ ( 1 ) Điều kiện phương trình có nghiệm : USD \ left | \ frac { c } { \ sqrt { a ^ { 2 } + b ^ { 2 } } } \ right | \ leqslant 1 \ Rightarrow \ left | c \ right | \ leqslant \ sqrt { a ^ { 2 } + b ^ { 2 } } \ Rightarrow c ^ { 2 } \ leqslant a ^ { 2 } + b ^ { 2 } $ Suy ra được điều kiện kèm theo để phương trình asinx + bcosx = c có nghiệm Công thức đặc biệt quan trọng : • sin ⁡ x + cos ⁡ x = 0 ⇔ x = – π4 + kπ ( k ∈ Z ) . • sin ⁡ x – cos ⁡ x = 0 ⇔ x = π4 + kπ Ví dụ : Hãy giải phương trình sau : ( 1 + $ \ sqrt { 3 } $ ) sinx + ( 1 - $ \ sqrt { 3 } $ ) cosx = 2 Giải :

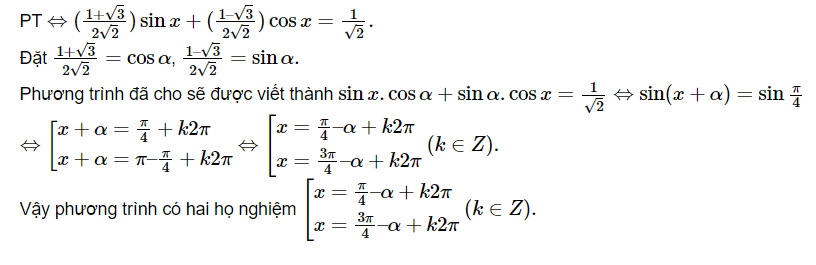
2. Phương trình bậc hai một số hàm lượng giác 

Dạng 1 : USD asin ^ { 2 } x + bsinx + c USD ( a ≠ 0 ; a, b, c ∈ R )

Phương pháp giải: 

Đặt :

• t = sin ⁡ x, với điều kiện kèm theo | t | ≤ 1, sau đó đưa phương trình USD asin ^ { 2 } x + bsinx + c USD về phương trình bậc hai theo t .
• Giải phương trình tìm ra t, quan tâm tích hợp điều kiện kèm theo của t rồi tìm x .

Dạng 2 : USD acos ^ { 2 } x + bcosx + c USD, ( a ≠ 0 ; a, b, c ∈ R ) .
Phương pháp giải : Đặt t = cos ⁡ x, điều kiện kèm theo | t | ≤ 1

• Đưa phương trình USD acos ^ { 2 } x + bcosx + c USD về phương trình bậc hai theo t .
• Giải phương trình ra tìm t, chú ý quan tâm tích hợp điều kiện kèm theo của t rồi tìm x .

Dạng 3 : USD atan ^ { 2 } x + btanx + c USD ( a ≠ 0 ; a, b, c ∈ R ) .
Phương pháp giải : Điều kiện cos ⁡ x ≠ 0

 ⇔x≠π2+kπ (k∈Z).

• Đặt t = tan ⁡ x ( t ∈ R ), đưa phương trình USD atan ^ { 2 } x + btanx + c USD về phương trình bậc hai theo t. Chú ý rằng khi tìm được nghiệm x cần thử lại vào điều kiện kèm theo xem có thoả mãn hay không .

Dạng 4 : USD acot ^ { 2 } x + bcotx + c USD ( a ≠ 0 ; a, b, c ∈ R ) .
Phương pháp giải : Điều kiện sin ⁡ x ≠ 0 ⇔ x ≠ kπ ( k ∈ Z ) .

• Đặt t = cot ⁡ x ( t ∈ R ), ta đưa phương trình USD acot ^ { 2 } x + bcotx + c USD về phương trình bậc hai theo ẩn t
• Giải ra t rồi tìm x, quan tâm khi tìm được nghiệm cần thử lại vào điều kiện kèm theo xem có thoả mãn hay không .

Ví dụ : Hãy giải phương trình USD 2 cos ^ { 2 } x-3cosx+1 USD
Giải :

3. Phương trình lượng giác thuần bậc hai đối với sinx và cosx

Phương trình thuần nhất bậc hai với sin ⁡ x và cos ⁡ x là phương trình có dạng : USD asin ^ { 2 } x + bsinx.cosx + ccos ^ { 2 } x = d USD, trong đó có : a, b, c, d cùng thuộc R .
Phương pháp giải :

Ta chia từng vế của phương trình cho một trong ba $sin^{2}x$, $cos^{2}x$ hoặc sin⁡x.cos⁡x. Ví dụ nếu ta chia cho $cos^{2}x$ ta làm theo các bước sau:

• Cho : cos ⁡ x = 0 ⇔ x = 2 + kπ ( k ∈ Z ) xem nó có phải là nghiệm của phương trình USD asin ^ { 2 } x + bsinx.cosx + ccos ^ { 2 } x = d USD không ?
• Với cos ⁡ x ≠ 0, chia cả hai vế cho USD cos ^ { 2 } x USD, lúc này phương trình USD asin ^ { 2 } x + bsinx.cosx + ccos ^ { 2 } x = d USD trở thành : USD atan ^ { 2 } x + btanx + c = d ( 1 + tan2x ) USD

⇔ USD ( a-d ) tan ^ { 2 } x + btanx + c-d = 0 USD .
Ta xét thấy, phương trình có dạng bậc hai theo tan .
Ví dụ : Hãy giải phương trình USD 2 \ sqrt { 3 } cos ^ { 2 } x + 6 sinxcosx = 3 + \ sqrt { 3 } $

4. Phương trình đối xứng với sinx và cosx

Phương trình đối xứng với sin ⁡ x và cos ⁡ x là phương trình dạng a ( sin ⁡ x + cos ⁡ x ) + bsin ⁡ xcos ⁡ x + c = 0, với a, b, c thuộc R .
Phương pháp giải :
Do : USD ( sinx + cosx ) ^ { 2 } $
= 1 + 2 sin ⁡ x.cos ⁡ x nên ta đặt :
t = sin ⁡ x + cos ⁡ x = $ \ sqrt { 2 } sin ( x + \ frac { \ pi } { 4 } ) = 2 cosz ( \ frac { \ pi } { 4 } – x ) USD
Điều kiện | t | ≤ 2 .
Nên sin ⁡ x.cos ⁡ x = $ \ frac { t ^ { 2 } – 1 } { 2 } $ và phương trình a ( sin ⁡ x + cos ⁡ x ) + bsin ⁡ xcos ⁡ x + c = 0 được viết lại là USD bt ^ { 2 } + 2 at – ( b + 2 c ) = 0 USD
Ví dụ : Giải pt sin ⁡ x + cos ⁡ x – 2 sin ⁡ x.cos ⁡ x + 1 = 0
Giải :

5. Phương trình lượng giác dạng thuận nghịch

Ta có dạng phương trình thuận nghịch là :
USD A ( f ^ { 2 } ( x ) + \ frac { k ^ { 2 } } { f ^ { 2 } ( x ) } ) + B ( f ( x ) + \ frac { k } { f ( x ) } ) + C = 0 USD ( 1 )
Hoặc $ A ( a ^ { 2 } tan ^ { 2 } x + b ^ { 2 } cot ^ { 2 } x ) + B ( atanx + bcotx ) + C = 0 USD ( 2 )
Giải :

• Đối với ( 1 ) : Đặt t = f ( x ) + $ \ frac { k } { f ( x ) } $
• Đối với ( 2 ) : Đặt t = a tanx + b cotx

Ví dụ : Giải phương trình $ \ frac { 3 } { cos ^ { 2 } x } + 3 cot ^ { 2 } x + 4 ( tanx + cotx ) – 1 = 0 USD
Giải :

6. Phương trình đẳng cấp bậc hai đối với sinx và cosx

Phương trình đẳng cấp bậc 2 so với sinx và cosx là phương trình có dạng :

USD asin ^ { 2 } x + bsinx.cosx + ccos ^ { 2 } x = d USD
Trong đó : x là một ẩn số
a, b, c, d là thông số
Giải :

• Trường hợp 1 : a = d

Lúc này phương trình có dạng :
USD asin ^ { 2 } x + bsinx.cosx + ccos ^ { 2 } x = a USD
USD \ Leftrightarrow asin ^ { 2 } x + bsinx.cosx + ccos ^ { 2 } = asin ^ { 2 } x + acos ^ { 2 } x USD
USD \ Leftrightarrow bsinx.cosx + ( c-a ) cos ^ { 2 } x = 0 USD
USD \ Leftrightarrow cosx \ left [ bsinx + ( c-a ) cosx \ right ] = 0 USD
USD \ Leftrightarrow cosx = 0 USD hoặc $ [ bsinx + ( c-a ) cosx \ right ] = 0 USD
Trường hợp 2 : USD a \ neq d USD
USD \ Leftrightarrow asin ^ { 2 } x + bsinx.cosx + ccos ^ { 2 } x = dsin ^ { 2 } x + dcos ^ { 2 } x USD
USD \ Leftrightarrow ( a-d ) sin ^ { 2 } x + bsinxcosx + ( c-d ) cos ^ { 2 } x = 0 USD
Có thể thấy cosx = 0 không phải là nghiệm phương trình, ta chia cả 2 vế cho cos ^ { 2 } x ta được :
USD ( a-d ) tan ^ { 2 } x + btanx + c-d = 0 USD
Ví dụ : Giải phương trình : USD 6 sin ^ { 2 } x + 14 sinxcosx – 4 ( 1 + cos2x ) = 6 USD

Giải:

PT $\Leftrightarrow 3(1-cos2x)+7 sin2x-4(1+cos2x)=6$
$\Leftrightarrow 7sin2x-7cos2x=7$
$\Leftrightarrow sin2x-cos2x=1$
$\Leftrightarrow sin(2x-\frac{\pi }{4})=\frac{1}{\sqrt{2}}$
$\Leftrightarrow x=\frac{\pi }{4}+k\pi$ hoặc $x=\frac{\pi }{2}+k\pi$

Bài viết trên đã tổng hợp lý thuyết cũng như các dạng toán về phương trình lượng giác thường gặp. Hy vọng rằng các em sẽ tiếp thu bài học kinh nghiệm thuận tiện hơn và giải bài tập thật thành thạo. Truy cập ngay nền tảng học trực tuyến Vuihoc. vn để để ôn tập nhiều hơn về các dạng toán khác nhé ! Chúc các bạn ôn tập hiệu suất cao .

>> Xem thêm: 

Source: http://wp.ftn61.com
Category: Hỏi Đáp