Lý thuyết & Phương pháp giải
1. Phương trình bậc nhất hai ẩn
Phương trình bậc nhất hai ẩn x, y có dạng tổng quát là
ax + by = c (1)
Bạn đang đọc: Cách giải và biện luận hệ phương trình bậc nhất cực hay
trong đó a, b, c là các thông số, với điều kiện kèm theo a và b không đồng thời bằng 0 .
CHÚ Ý
a. Khi a = b = 0 ta có phương trình 0 x + 0 y = c. Nếu c ≠ 0 thì phương trình này vô nghiệm, còn nếu c = 0 thì mọi cặp số ( x0 ; y0 ) đều là nghiệm .
b. Khi b ≠ 0, phương trình ax + by = c trở thành
y = ( – a / b ) x + c / b ( 2 )
Cặp số ( x0 ; y0 ) là một nghiệm của phương trình ( 1 ) khi và chỉ khi điểm M ( x0 ; y0 ) thuộc đường thẳng ( 2 ) .
Tổng quát, người ta chứng tỏ được rằng phương trình bậc nhất hai ẩn luôn luôn có vô số nghiệm. Biểu diễn hình học tập nghiệm của phương trình của phương trình ( 1 ) là một đường thẳng trong mặt phẳng tọa độ Oxy .
2. Hệ hai phương trình bậc nhất hai ẩn
Hệ phương trình bậc nhất hai ẩn có dạng tổng quát là
Trong đó x, y là hai ẩn ; các chữ số còn lại là thông số .
Nếu cặp số ( x0 ; y0 ) đồng thời là nghiệm của cả hai phương trình của hệ thì ( x0 ; y0 ) được gọi là một nghiệm của hệ phương trình ( 1 ) .
Giải hệ phương trình ( 1 ) là tìm tập nghiệm của nó
Công thức nghiệm : Quy tắc Crame .
| Xét D | Kết quả | |
| D ≠ 0 | Hệ có nghiệm duy nhất x = Dx/D, y = Dy/D | |
| D = 0 | Dx ≠ 0 hoặc Dy ≠ 0 | Hệ vô nghiệm. |
| Dx = Dy = 0 | Hệ có vô số nghiệm. | |
Để giải hệ phương trình bậc nhất hai ẩn ta hoàn toàn có thể dùng các cách giải đã biết như : chiêu thức thế, giải pháp cộng đại số .
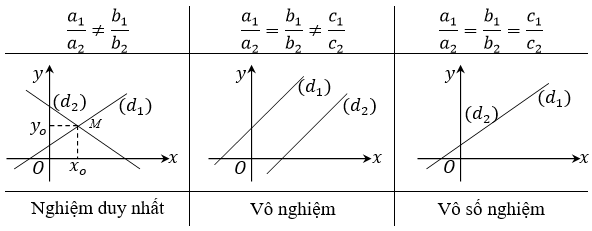
Biểu diễn hình học của tập nghiệm :
Nghiệm ( x ; y ) của hệ ( I ) là tọa độ điểm M ( x ; y ) thuộc cả 2 đường thẳng :
( d1 ) : a1x + b11y = c1 và ( d2 ) : a2x + b2y = c2
+ Hệ ( I ) có nghiệm duy nhất ⇔ ( d1 ) và ( d2 ) cắt nhau .
+ Hệ ( I ) vô nghiệm ⇔ ( d1 ) và ( d2 ) song song với nhau .
+ Hệ ( I ) có vô số nghiệm ⇔ ( d1 ) và ( d2 ) trùng nhau .
3. Hệ ba phương trình bậc nhất ba ẩn
Phương trình bậc nhất ba ẩn có dạng tổng quát là
ax + by + cz = d
trong đó x, y, z là ba ẩn ; a, b, c, d là các thông số và a, b, c không đồng thời bằng 0
Hệ phương trình bậc nhất ba ẩn có dạng tổng quát là
Trong đó x, y, z là ba ẩn ; các chữ còn lại là các thông số .
Mỗi bộ ba số ( x0, y0, z0 ) nghiệm đúng của ba phương trình của hệ được gọi là một nghiệm của hệ phương trình ( 2 ) .
Phương pháp giải
Nguyên tắc chung để giải các hệ phương trình nhiều ẩn là khử bớt ẩn để đưa về các phương trình hay hệ phương trình có số ẩn ít hơn. Để khử bớt ẩn, ta cũng hoàn toàn có thể dùng các giải pháp cộng đại số, giải pháp thế như so với hệ phương trình bậc nhất hai ẩn .

Ví dụ minh họa
Bài 1: Cho hệ phương trình 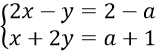
Hướng dẫn:
Ta có :
Đẳng thức xảy ra khi a = 1/2
Bài 2: Giải hệ phương trình
Hướng dẫn:
ĐK : xy ≠ 0. Khi đó
Bài 3: Có bao nhiêu cặp số nguyên (a; b) sao cho hệ phương trình
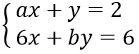
Hướng dẫn:
Ta có ax + y = 2 ⇒ y = 2 – ax
Thay vào phương trình 6 x + by = 6 có
6 x + b ( 2 – ax ) = 6 ⇔ x ( 6 – ab ) + 2 b – 6 = 0
Hệ vô nghiệm khi và chỉ khi phương trình x ( 6 – ab ) + 2 b – 6 = 0 vô nghiệm
Do ( a ; b ) nguyên nên ( a ; b ) = { ( 6 ; 1 ) ; ( 1 ; 6 ) ; ( – 6 ; – 1 ) ; ( – 1 ; – 6 ) ; ( – 2 ; – 3 ) ; ( – 3 ; – 2 ) ; ( 3 ; 2 ) }
Bài 4: Gọi (x0; y0; z0) là nghiệm của hệ phương trình
Tính giá trị của biểu thức P = x0y0z0
Hướng dẫn:
Ta có
Phương trình ( 3 ) ⇔ z = 24 – 3 x – 2 y. Thay vào ( 1 ) và ( 2 ) ta được hệ phương trình
Suy ra z = 24 – 3.4 – 2.5 = 2
Vậy hệ phương trình có nghiệm ( x ; y ; z ) = ( 4 ; 5 ; 2 ) → P = 4.5.2 = 40
Bài 5: Tìm giá trị thực của tham số m để hệ phương trình
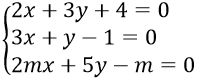
Hướng dẫn:
Từ hệ phương trình đã cho ta suy ra
Hệ phương trình
Có nghiệm duy nhất khi ( 1 ; – 2 ) là nghiệm của phương trình 2 mx + 5 y – m = 0 tức là 2 m. 1 + 5. ( – 2 ) – m = 0 ⇔ m = 10
Bài 6: Giải hệ phương trình
Hướng dẫn:
a. Ta có : y = 1 – √ 2 x ⇒ 3 x + √ 2 ( 1 – √ 2. x ) = 2 ⇒ x = 2 – √ 2 ⇒ y = 3 – 2 √ 2
b. Ta có : Thế y = 4 – 2 x vào phương trình y + z = 2 + √ 2 ta được – 2 x + z = – 2 + √ 2
Giải hệ 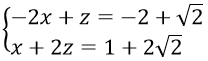
Source: http://wp.ftn61.com
Category: Hỏi Đáp
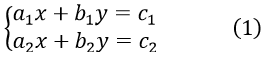
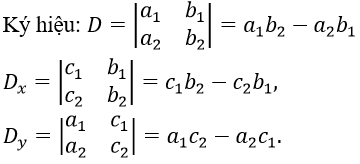
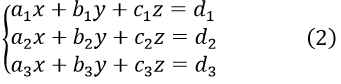
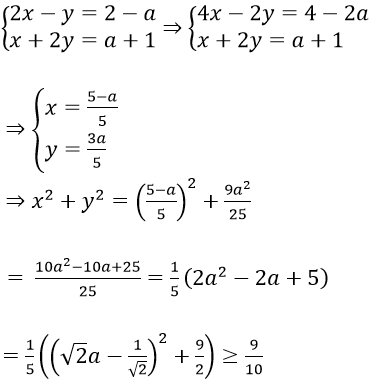
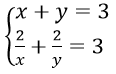
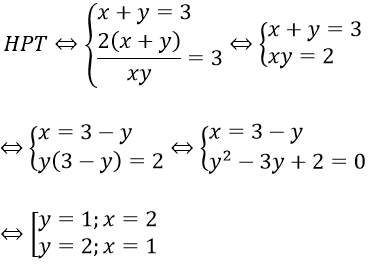
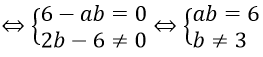
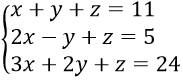
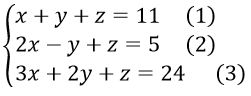
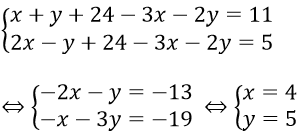
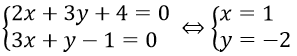
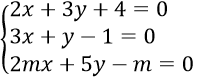
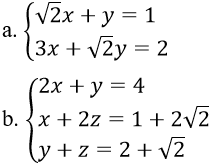



Để lại một bình luận