Tổng hợp cách giải hệ phương trình bậc nhất 3 ẩn | Bán Máy Nước Nóng – Banmaynuocnong

Cách giải hệ phương trình bậc nhất 3 ẩn

Phương trình phương trình bậc nhất nhiều ẩn

A. KIẾN THỨC CẦN NHỚ

1. phương trình bậc nhất hai ẩn x, y có dạng

ax + by = c .

trong đó a, b, c là các số thực đã cho và a, b không đồng thời bằng 0

2. Hệ phương trình bậc nhất hai ẩn x, y có dạng

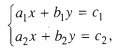
trong đó cả hai phương trình đều là phương trình bậc nhất hai ẩn
Có hai cách giải hệ phương trình bậc nhất hai ẩn quen thuộc
a ) Phương pháp thế. Từ một phương trình của hệ bộc lộ một ẩn qua ẩn kia rồi thay vào phương trình còn lại .
b ) Phương pháp cộng. Biến đôi cho thông số của một ẩn trong hai phương trình là hai số đối nhau rồi cộng từng vế hai phương trình lại .

3. Dạng tam giác của hệ ba phương trình bậc nhất ba ẩn là

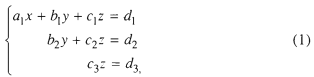
hoặc

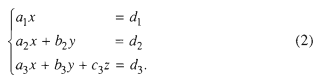
Cách giải. Từ phương trình cuối của hệ ( 1 ) tính được z, thay vào phương trình thứ hai tính được y tồi thay vào phương trình đầu rồi tính được x .
Từ phương trình đầu của hệ ( 2 ) tính được x, thay vào phương trình thứ hai tính được y rồi thay vào phương trình thứ 3 tính được z .
Hệ ba phương trình bậc nhất ba ẩn có dạng :

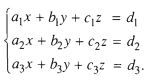
Cách giải. Dùng chiêu thức Gau-xơ khử dần ẩn số để đưa về hệ phương trình dạng tam giác .

B. BÀI TẬP MẪU

BÀI 1.

Giải các hệ phương trình

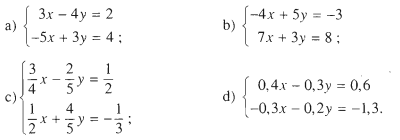
Giải

a ) Từ phương trình thứ nhất suy ra

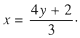
Thay biểu thức của x vào phương trình thứ 2 ta được

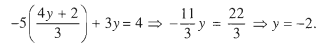
Từ đó

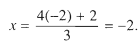
Vậy nghiệm của phương trình là ( – 2 ; – 2 )
b ) Từ đó .

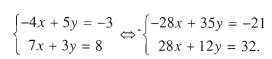
Cộng từng vế hai phương trình ta được 47 y = 11 ⇔ 11/47
Thay y = 11/47 vào một trong hai phương trình của hệ đã cho ta được x = 49/47

c ) ta có

Cộng từng vế hai phương trình ta được – 1,7 y = – 3,4 suy ra y = 2
Thay y = 2 vào một trong hai phương trình của hệ, ta được x = 3 .
Vậy nghiệm của hệ phương trình là ( 3 ; 2 ) .

BÀI 2.

Tìm một số ít có hai chữ số, biết hiệu của hai chữ số đó bằng 3. Nếu viết các chữ số theo thứ tự ngược lại thì được một số ít bằng 4/5 số bắt đầu trừ đi 10 .

Giải

Gọi chữ số hàng chục là x chữ số hàng đơn vị chức năng là y thì số phải tìm là l0x + y. Điều kiện bài toán là X, V nguyên và 1 ≤ x ≤ 9, 0 ≤ y ≤ 9
Số khởi đầu là 10 x + y thì số viết theo thứ tự ngược lại là 10 y + y
Theo giả thiết số viết theo thứ tự ngược lại phải nhỏ hơn số bắt đầu. cho nên vì thế phải có x > y. Ta có hệ phương trình :

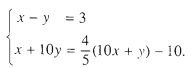
Thay x = y + 3 vào phương trình thứ hai của hệ, ta được
11 y = 55 ⇒ y = 5 ⇒ x = 8 .
Vậy số phải tìm là 85 .

BÀI 3.

Giải hệ phương trình

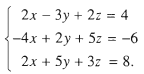
Giải

Nhân hai vế của phương trình đầu với 2 rồi cộng từng vế với phương trình thứ hai, ta được hệ phương trình

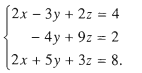
Nhân hai vế của phương trình đầu với – 1 rồi cộng từng vế với phương trình thứ ba, ta được hệ phương trình

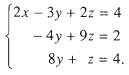
Như vậy, ta đã khử được ẩn x trong hai phương trình cuối. Để khử ẩn y trong phương trình thứ ba, ta nhân hai vế của phương trình thứ hai với 2 rồi cộng từng vế vói phương trình thứ ba ta được hệ phương trình có dạng tam giác

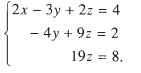
Từ phương trình sau cuối suy ra z = 8/19. Thay giá trị này của z vào phương trình thứ 2, ta được y = 17/38. Cuối cùng, thay các giá trị của y và z vừa tìm được vào phương trình đầu ta tìm được x = 171 / 76
Vậy nghiệm của phương trình là

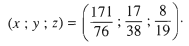
BÀI 4.

Giải hệ phương trình

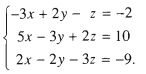
Giải

Nhận xét. Đối với hệ phương trình này, việc khử ẩn x không đơn thuần lắm. Tuy nhiên, nếu quan tâm đến thông số của z ở ba phương trình, ta thấy dễ khử ẩn z ở hai phương trình cuối .
Nhân hai vế của phương trình đầu với 2 rồi cộng từng vế với phương trình thứ hai. Nhân hai vế của phương trình đầu với – 3 rồi cộng từng vế với phương trình thứ ba, ta được hệ phương trình

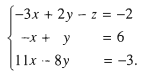
Đến đây, ta thấy dễ khử ẩn x ( hoặc ẩn y ) trong phương trình thứ ba. Chẳng hạn, nhân hai vế của phương trình thứ hai với 8 rồi cộng từng vế với phương trình thứ ba, ta được

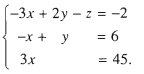
Hệ phương trình này có dạng tam giác. Giải lần lượt từ phương trình thứ ba lên ta được x = 15, y = 21, z = – 1
Đáp số : ( x ; y ; z ) = ( 15 ; 21 ; – 1 )

BÀI 5.

Ba cò Lan. Hương và Thuý cùng thêu một loại áo giống nhau. Số áo của Lan thêu trong 1 giờ ít hơn tổng số áo của Hường và Thuý thêu trong 1 giờ là 5 áo. Tổng số áo của Lan thêu trong 4 giờ và Hương thêu trong 3 giờ nhiều hơn số áo cua Thuý thêu trong 5 giờ là 30 áo. Số áo của Lan thêu trong 2 giờ cộng với số áo của Hương thêu trong 5 giờ và số áo của Thuý thêu trong 3 giờ tổng thể được 76 áo. Hỏi trong 1 giờ mỗi cỏ thêu được mấy áo ?

Giải

Gọi x, y, z lần lượt là số áo của Lan, Hương, Thúy thêu trong 1 giờ. Điều kiện là x, y, z nguyên dương .
Từ giả thiết của bài toán ta có

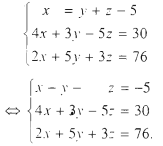
Đưa về tam giác, ta được hệ phương trình

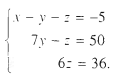
Hệ này có nghiệm ( x ; y ; z ) = ( 9 ; 8 ; 6 ) .
Kết luận. Trong một giờ, Lan thêu được 9 áo. Hương thêu được 8 áo. Thúy thêu được 6 áo .

C. BÀI TẬP

3.26 Một công ty có 85 xe chở khách gồm hai loại, xe chở được 4 khách và xe chở được 7 khách. Dùng tất cả số xe đó. tối đa công ty chở một lần được 445 khách. Hỏi công ty đó có mấy xe mỗi loại ?

⇒ Xem đáp án tại đây .

3.27 Giải các hệ phương trình:

⇒ Xem đáp án tại đây .

3.28. Giải các hệ phương trình sau bằng máy tính bỏ túi

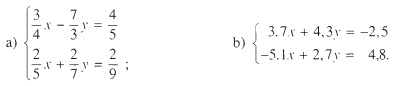
⇒ Xem đáp án tại đây .

3.29. Giải các hệ phương trình sau bằng máy tính bỏ túi:

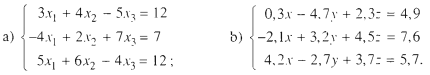
⇒ Xem đáp án tại đây .

3.30

Một chủ shop kinh doanh bán lẻ mang 1 500 000 đồng đến ngân hàng nhà nước đổi tiền xu để trả lại cho người mua. Ông ta đổi được tổng thể 1 450 đồng xu tiền xu các loại 2000 đồng, 1000 đồng và 500 đồng. Biết rằng số tiền xu loại 1 000 đồng bằng hai lần hiệu của số tiền xu loại 500 đồng với số tiền xu loại 2000 đồng. Hỏi mỗi loại có bao nhiêu đồng xu tiền xu ?
⇒ Xem đáp án tại đây .

3.31

Tìm giá trị của m để các hệ phương trình sau vô nghiệm

⇒ Xem đáp án tại đây .

Bài tập trắc nghiệm

3.32. Hệ phương trình

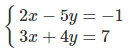
có nghiệm là :

⇒ Xem đáp án tại đây .

3.33 Nghiệm của hệ phương trình

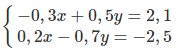
A. x = 2, y = – 3 B. x = – 2, y = 3 C. x = – 1, y = – 2 D. x = 1, y = 5
⇒ Xem đáp án tại đây .

3.34. Hệ phương trình

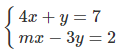
vô nghiệm khi m nhận giá trị :
A. m = 4 B. m = – 3 C. m = 2 D. m = – 12
⇒ Xem đáp án tại đây .

3.35

Một công ti kinh doanh thương mại xe buýt có 35 xe gồm hai loại : loại xe chở được 45 khách và loại xe chở được 12 khách. Nếu dùng toàn bộ số xe đó tối đa công ti chở một lần được 1113 khách. Vậy công ti có số xe mỗi loại là :
A. 20 xe 45 chỗ, 15 xe 12 chỗ .
B. 17 xe 45 chỗ, 18 xe 12 chỗ .
C. 21 xe 45 chỗ, 14 xe 12 chỗ .
D. 19 xe 45 chỗ, 16 xe 12 chỗ .
⇒ Xem đáp án tại đây .

3.36 Hệ phương trình

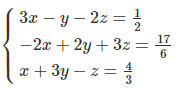
có nghiệm là :

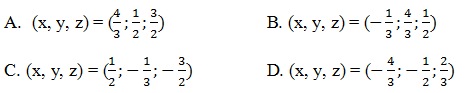
⇒ Xem đáp án tại đây .

3.37. Một khách sạn có 102 phòng gồm ba loại : phòng 3 ngựời, phòng 2 người và phòng 1 người. Nếu đầy khách tất cả các phòng thì khách sạn đón được 211 khách. Còn nếu cải tạo lại các phòng bằng cách : sửa các phòng 2 người thành phòng 3 người, còn phòng 3 người sửa lại thành phòng 2 người và giữ nguyên các phòng 1 người thì tối đa một lần có thể đón đến 224 khách.

Vậy số phòng từng loại lúc bấy giờ của khách sạn là
A. 50 phòng 3 người, 41 phòng 2 người, 11 phòng 1 người .
B. 32 phòng 3 người, 45 phòng 2 người, 25 phòng 1 người ,
C. 41 phòng 3 người, 51 phòng 2 người, 10 phòng 1 người .
D. 25 phòng 3 người, 59 phòng 2 người, 18 phòng 1 người .

⇒ Xem đáp án tại đây.

3.38.

Một số có ba chữ số. Nếu lấy số đó chia cho tổng các chữ số của nó thì được thương là 17 và dư 5. Nếu đổi hai chữ số hàng chục và hàng trăm cho nhau thì được số mới mà chia cho tổng các chữ số của nó thì được thương là 30 và dư là 4. Nếu đổi hai chữ số hàng chục và hàng đơn vị chức năng của số mới này cho nhau thì được một số ít mà chia cho tổng các chữ số của nó thì được thương là 34 và dư là 3. Vậy số đã cho khởi đầu là : A. 172 ; B. 296 ; C. 124 ; D. 587 .
⇒ Xem đáp án tại đây .

Source: http://wp.ftn61.com
Category: Hỏi Đáp