Phương trình đường tròn và các dạng bài tập có lời chuẩn 100%

Bạn gặp rắc rối về giải bài tập viết phương trình đường tròn nhưng bạn lúng túng không biết viết như thế nào ? Cho nên, chúng tôi sẽ san sẻ kim chỉ nan phương trình đường tròn và các dạng bài tập có giải thuật cụ thể để các bạn cùng tìm hiểu thêm nhé

Lý thuyết phương trình đường tròn

1. Phương trình đường tròn có tâm và bán kính cho trước

Trong mặt phẳng Oxy, đường tròn (C ) tâm I(a; b) bán kính R có phương trình: (x – a)2 + (y – b)2 = R2

Lưu ý. Phương trình đường tròn có tâm là gốc tọa độ O và bán kính R là x2 + y2 = R2

2. Nhận xét

+ ) Phương trình đường tròn ( x – a ) 2 + ( y – b ) 2 = R2 hoàn toàn có thể viết dưới dạng : x2 + y2 – 2 ax – 2 by + c = 0. Trong đó c = a2 + b2 – R2 .
+ ) Phương trình x2 + y2 – 2 ax – 2 by + c = 0 là phương trình của đường tròn ( C ) khi a2 + b2 – c2 > 0. Khi đó, đường tròn ( C ) có tâm I ( a ; b ), nửa đường kính R = √ a2 + b2 – c

3. Phương trình tiếp tuyến của đường tròn

Cho điểm M0 ( x0 ; y0 ) nằm trên đường tròn ( C ) tâm I ( a ; b ). Gọi ∆ là tiếp tuyến với ( C ) tại M0 .

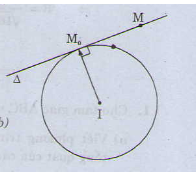
Ta có M0 thuộc Δ và vectơ IM0 → = ( x0 − a ; y0 − b ) là vectơ pháp tuyến cuả Δ
Do đó Δ có phương trình là :
( x0 − a ) ( x − x0 ) + ( y0 − b ) ( y − y0 ) = 0
Phương trình ( 1 ) là phương trình tiếp tuyến của đường tròn ( x − a ) 2 + ( y − b ) 2 = R2 tại điểm M0 nằm trên đường tròn .

Tham khảo thêm:

Các dạng bài tập phương trình đường tròn

1. Dạng 1: Tìm tâm và bán kính của đường tròn

Phương pháp:

Ví dụ : Tìm tâm và nửa đường kính của các đường tròn sau :
a. x2 + y2 − 2 x − 2 y − 2 = 0
b. 16×2 + 16 y2 + 16 x − 8 y − 11 = 0
c. x2 + y2 − 4 x + 6 y − 3 = 0 .
Lời giải :
a. Ta có : − 2 a = − 2 ⇒ a = 1
− 2 b = − 2 ⇒ b = 1 ⇒ I ( 1 ; 1 )
R2 = a2 + b2 − c = 12 + 12 − ( − 2 ) = 4 ⇒ R = √ 4 = 2
Cách khác :
x2 + y2 − 2 x − 2 y − 2 = 0 ⇔ ( x2 − 2 x + 1 ) + ( y2 − 2 y + 1 ) = 4 ⇔ ( x − 1 ) 2 + ( y − 1 ) 2 = 22
Vậy đường tròn có tâm I ( 1 ; 1 ) nửa đường kính R = 2 .
b. 16×2 + 16 y2 + 16 x − 8 y − 11 = 0
⇔ x2 + y2 + x − ½y − 11/16 = 0
− 2 a = 1 ⇒ a = − ½
− 2 b = − ½ ⇒ b = ¼
⇒ I ( − ½ ; ¼ )
R2 = a2 + b2 − c = ( − ½ ) 2 + ( ¼ ) 2 − ( − 11/16 ) = 1 ⇒ R = √ 1 = 1
Cách khác

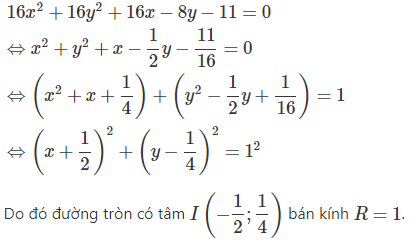
c. x2 + y2 − 4 x + 6 y − 3 = 0 .
− 2 a = − 4 ⇒ a = 2
− 2 b = 6 ⇒ b = − 3
⇒ I ( 2 ; − 3 )
R2 = a2 + b2 − c = 22 + ( − 3 ) 2 − ( − 3 ) = 16
⇒ R = √ 16 = 4
Cách khác :
x2 + y2 − 4 x + 6 y − 3 = 0 .
⇔ ( x2 − 4 x + 4 ) + ( y2 + 6 y + 9 ) = 16
⇔ ( x − 2 ) 2 + ( y + 3 ) 2 = 42
Do đó đường tròn có tâm I ( 2 ; − 3 ) nửa đường kính R = 4 .

2. Dạng 2: Viết phương trình đường tròn

Cách 1 :
Tìm tọa độ tâm I ( a ; b ) của đường tròn ( C )
Tìm nửa đường kính R của ( C )
Viết phương trình ( C ) theo dạng : ( x – a ) 2 + ( y – b ) 2 = R2 ( 1 )
Chú ý :

• (C) đi qua A, B ⇔ IA2 = IB2 = R2.
• (C) đi qua A và tiếp xúc với đường thẳng ∆ tại A ⇔ IA = d(I, ∆).
• (C) tiếp xúc với hai đường thẳng ∆1 và ∆2

⇔ d ( I, ∆ 1 ) = d ( I, ∆ 2 ) = R
Cách 2 :
Gọi phương trình đường tròn ( C ) là x2 + y2 – 2 ax – 2 by + c = 0 ( 2 )
Từ điều kiện kèm theo của đề bài đưa đến hệ phương trình với ba ẩn số là : a, b, c

Giải hệ phương trình tìm a, b, c để thay vào (2), ta được phương trình đường tròn (C)

Ví dụ 1 : Lập phương trình đường tròn ( C ) trong các trường hợp sau :

a. (C) có tâm I(−2;3) và đi qua M(2;−3);
b.(C) có tâm I(−1;2) và tiếp xúc với đường thẳng d:x–2y+7=0
c. (C) có đường kính AB với A(1;1) và B(7;5).

Lời giải
a. Đường tròn ( C ) có tâm I ( a ; b ) và đi qua điểm M thì có nửa đường kính là R = IM và có phương trình :
( x − a ) 2 + ( y − b ) 2 = R2 = IM2 .
( C ) có tâm I và đi qua M nên nửa đường kính R = IM .
⇒ R2 = IM2 = ( 2 + 2 ) 2 + ( − 3 − 32 ) = 52
Phương trình ( C ) : ( x + 2 ) 2 + ( y − 3 ) 2 = 52
b. Đường tròn ( C ) có tâm I ( a ; b ) và tiếp xúc với đường thẳng d thì R = d ( I ; d ) .
Đường tròn tiếp xúc với đường thẳng d
⇒ d ( I ; d ) = R

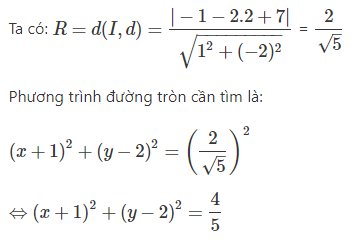
c. Đường tròn ( C ) có đường kính AB thì có tâm I là trung điểm của AB và nửa đường kính : R = AB / 2 .
Tâm I là trung điểm của AB, có tọa độ :

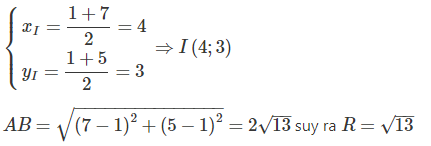
Phương trình cần tìm là : ( x − 4 ) 2 + ( y − 3 ) 2 = 13
Ví du : Lập phương trình đường tròn đi qua ba điểm : A ( 1 ; 2 ) ; B ( 5 ; 2 ) ; C ( 1 ; − 3 )
Lời giải :
Gọi phương trình đường tròn có dạng : ( C ) : x2 + y2 − 2 ax – 2 by + c = 0
A ( 1 ; 2 ) ∈ ( C ) nên : 12 + 22 – 2 a − 4 b + c = 0 ⇔ 2 a + 4 b – c = 5
B ( 5 ; 2 ) ∈ ( C ) nên : 52 + 22 – 10 a − 4 b + c = 0 ⇔ 10 a + 4 b – c = 29
C ( 1 ; − 3 ) ∈ ( C ) nên : 12 + ( − 3 ) 2 – 2 a + 6 b + c = 0 ⇔ 2 a − 6 b – c = 10

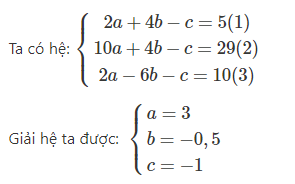
Phương trình cần tìm là : x2 + y2 − 6 x + y − 1 = 0

3. Dạng 3: Viết phương trình tiếp tuyến của đường tròn.

Loại 1 : Lập phương trình tiếp tuyến tại điểm Mo ­ ( xo ; yo ) thuộc đường tròn ( C )
Tìm tọa độ tâm I ( a, b ) của đường tròn ( C )
Phương trình tiếp tuyến với ( C ) tại Mo ­ ( xo ; yo ) có dạng :
( x0 – a ) ( x-x0 ) + ( y0 – b ) ( y – y0 ) = 0
Loại 2 : Lập phương trình tiếp tuyến của ∆ với ( C ) khi chưa biết tiếp điểm : dùng điều kiện kèm theo tiếp xúc với đường tròn ( C ) tâm I, nửa đường kính R ⇔ d ( I, ∆ ) = R
Ví dụ 1 : Cho đường tròn ( C ) : ( x – 3 ) 2 + ( y – 1 ) 2 = 10. Phương trình tiếp tuyến của ( C ) tại điểm A ( 4 ; 4 )
Lời giải :
Đường tròn ( C ) có tâm I ( 3 ; 1 ). Gọi d là tiếp tuyến của đường tròn ( C ) tại điểm A ; khi đó d và IA vuông góc với nhau .
⇒ IA → = ( 1 ; 3 ) là vectơ pháp tuyến của d .
Suy ra phương trình d : 1 ( x – 4 ) + 3 ( y – 4 ) = 0
Hay x + 3 y – 16 = 0 .
Ví dụ 2 : Cho đường tròn ( x – 3 ) 2 + ( y + 1 ) 2 = 5. Phương trình tiếp tuyến của ( C ) song song với đường thẳng d : 2 x + y + 7 = 0
Lời giải :
Do tiếp tuyến cần tìm song song với đường thẳng d : 2 x + y + 7 = 0 nên
phương trình tiếp tuyến có dạng ∆ : 2 x + y + m = 0 với m ≠ 7 .
Đường tròn ( C ) có tâm I ( 3 ; – 1 ) và nửa đường kính R = √ 5
Đường thẳng tiếp xúc với đường tròn ( C ) khi :

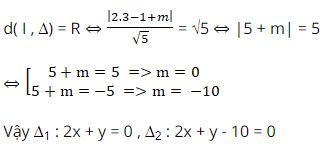
Sau khi đọc xong bài viết của chúng tôi các bạn hoàn toàn có thể mạng lưới hệ thống lại kiến thức và kỹ năng về phương trình đường tròn để vận dụng vào làm các dạng bài tập tương quan nhanh gọn nhé

Đánh giá bài viết

Source: http://wp.ftn61.com
Category: Hỏi Đáp