A. Phương pháp giải
* Để viết phương trình tổng quát của đường thẳng d ta cần xác lập :
– Điểm A ( x0 ; y0 ) thuộc d
– Một vectơ pháp tuyến n→( a; b) của d
Khi đó phương trình tổng quát của d là : a ( x-x0 ) + b ( y-y0 ) = 0
* Cho đường thẳng d : ax + by + c = 0 nếu đường thẳng d / / ∆ thì đường thẳng ∆ có dạng : ax + by + c ’ = 0 ( c ’ ≠ c ) .

B. Ví dụ minh họa
Ví dụ 1. Cho ba đường thẳng (a):3x – 2y + 5 = 0; (b): 2x + 4y – 7 = 0 và
( c ) : 3 x + 4 y – 1 = 0. Phương trình đường thẳng d đi qua giao điểm của a và b, và song song với c là :
A. 24x + 32y – 53 = 0. B. 23x + 32y + 53 = 0 C. 24x – 33y + 12 = 0. D. Đáp án khác
Lời giải
Giao điểm của ( a ) và ( b ) nếu có là nghiệm hệ phương trình :
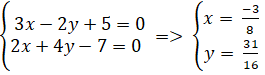
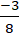
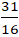
Ta có đường thẳng d / / c nên đường thẳng d có dạng : 3 x + 4 y + c = 0 ( c ≠ – 1 )
Vì điểm A thuộc đường thẳng d nên : 3. + 4. + c = 0 ⇔ c=
Vậy d : 3 x + 4 y + = 0 ⇔ d3 = 24 x + 32 y – 53 = 0
Chọn A.
Ví dụ 2: Viết phương trình tổng quát của đường thẳng ∆ đi qua M(1; -3) và nhận vectơ n→(1; 2) làm vectơ pháp tuyến.
A. ∆: x + 2y + 5 = 0 B. ∆: x + 2y – 5 = 0 C. ∆: 2x + y + 1 = 0 D. Đáp án khác
Lời giải
Đường thẳng ∆ : qua M ( 1 ; – 3 ) và VTPT n → ( 1 ; 2 )
Vậy phương trình tổng quát của đường thẳng ∆ là 1 ( x – 1 ) + 2 ( y + 3 ) = 0
Hay x + 2 y + 5 = 0
Chọn A.
Ví dụ 3: Cho đường thẳng (d): x-2y + 1= 0. Nếu đường thẳng (∆) đi qua M(1; -1) và song song với d thì ∆ có phương trình
A. x – 2y – 3 = 0 B. x – 2y + 5 = 0 C. x – 2y +3 = 0 D. x + 2y + 1 = 0
Lời giải
Do đường thẳng ∆ / / d nên đường thẳng ∆ có dạng x – 2 y + c = 0 ( c ≠ 1 )
Ta lại có M ( 1 ; – 1 ) ∈ ( ∆ ) ⇒ 1 – 2 ( – 1 ) + c = 0 ⇔ c = – 3
Vậy phương trình ∆ : x – 2 y – 3 = 0
Chọn A
Ví dụ 4: Cho ba điểm A(1; -2); B(5; -4) và C(-1;4). Đường cao AA’ của tam giác ABC có phương trình
A. 3x – 4y + 8 = 0 B. 3x – 4y – 11 = 0 C. -6x + 8y + 11 = 0 D. 8x + 6y + 13 = 0
Lời giải
Ta có BC → = ( – 6 ; 8 )
Gọi AA ’ là đường cao của tam giác ABC
⇒ AA ‘ nhận VTPT n → = BC → = ( – 6 ; 8 ) và qua A ( 1 ; – 2 )
Suy ra phương trình AA ’ : – 6 ( x – 1 ) + 8 ( y + 2 ) = 0
Hay – 6 x + 8 y + 22 = 0 ⇔ 3 x – 4 y – 11 = 0 .
Chọn B
Ví dụ 5. Đường thẳng d đi qua điểm A( 1; -3) và có vectơ pháp tuyến n→( 1; 5) có phương trình tổng quát là:
A. d: x + 5y + 2 = 0 B. d: x- 5y + 2 = 0 C. x + 5y + 14 = 0 D. d: x – 5y + 7 = 0
Lời giải
Ta có : đường thẳng d : qua A ( 1 ; – 3 ) và VTPT n → ( 1 ; 5 )
⇒ Phương trình tổng quát của đường thẳng d :
1 ( x – 1 ) + 5. ( y + 3 ) = 0 hay x + 5 y + 14 = 0
Chọn C.
Ví dụ 6. Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A(2; -1); B( 4; 5) và C( -3; 2). Lập phương trình đường cao của tam giác ABC kẻ từ A
A. 7x + 3y – 11 = 0 B. -3x + 7y + 5 = 0 C. 3x + 7y + 2 = 0 D. 7x + 3y + 15 = 0
Lời giải
Gọi H là chân đường vuông góc kẻ từ A .
Đường thẳng AH : qua A ( 2 ; – 1 ) và Nhận VTPT BC → ( 7 ; 3 )
⇒ Phương trình đường cao AH :
7 ( x – 2 ) + 3 ( y + 1 ) = 0 hay 7 x + 3 y – 11 = 0
Chọn A.
Ví dụ 7 : Cho tam giác ABC cân tại A có A(1 ; -2). Gọi M là trung điểm của BC và
M ( – 2 ; 1 ). Lập phương trình đường thẳng BC ?
A. x + y – 3 = 0 B. 2x – y + 6 = 0 C. x – y + 3 = 0 D. x + y + 1 = 0
Lời giải
+ Do tam giác ABC cân tại A nên đường trung tuyến AM đồng thời là đường cao
⇒ AM vuông góc BC .
⇒ Đường thẳng BC nhận AM → ( – 3 ; 3 ) = – 3 ( 1 ; – 1 ) làm VTPT
+ Đường thẳng BC : qua M ( – 2 ; 1 ) và VTPT n → ( 1 ; – 1 )
⇒ Phương trình đường thẳng BC :
1 ( x + 2 ) – 1 ( y – 1 ) = 0 hay x – y + 3 = 0
Chọn C.
Ví dụ 8 : Cho tam giác ABC có đường cao BH : x + y – 2 = 0, đường cao CK : 2x + 3y – 5 = 0 và phương trình cạnh BC : 2x – y + 2 = 0. Lập phương trình đường cao kẻ từ A của tam giác ABC ?
A. x – 3y + 1 = 0 B. x + 4y – 5 = 0 C. x + 2y – 3 =0 D. 2x – y + 1 = 0
Lời giải
+ Gọi ba đường cao của tam giác ABC đồng quy tại P. Tọa độ của P là nghiệm hệ phương trình :
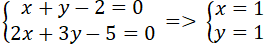
+ Tọa độ điểm B là nghiệm hệ phương trình :
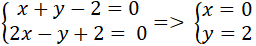
Tương tự ta tìm được tọa độ C(- 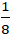
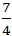
+ Đường thẳng AP :
⇒ Phương trình đường thẳng AP :
1 ( x – 1 ) + 2 ( y – 1 ) = 0 ⇔ x + 2 y – 3 = 0
Chọn C.
Ví dụ 9. Phương trình tổng quát của đường thẳng d đi qua O và song song với đường thẳng ∆ : 3x + 5y – 9 = 0 là:
A. 3x + 5y – 7 = 0 B. 3x + 5y = 0 C. 3x – 5y = 0 D. 3x – 5y + 9 = 0
Lời giải
Do đường thẳng d / / ∆ nên đường thẳng d có dạng : 3 x + 5 y + c = 0 ( c ≠ – 9 )
Do điểm O ( 0 ; 0 ) thuộc đường thẳng d nên :
3.0 + 5.0 + c = 0 ⇔ c = 0
Vậy phương trình đường thẳng d : 3 x + 5 y = 0
Chọn B.
Ví dụ 10: Cho tam giác ABC có B(-2; -4). Gọi I và J lần lượt là trung điểm của AB và AC. Biết đường thẳng IJ có phương trình 2x – 3y + 1 = 0. Lập phương trình đường thẳng BC?
A. 2x + 3y – 1 = 0 B. 2x – 3y – 8 = 0 C. 2x + 3y – 6 = 0 D. 2x – 3y + 1 = 0
Lời giải
Do I và J lần lượt là trung điểm của AB và AC nên IJ là đường trung bình của tam giác ABC .
⇒ IJ / / BC .
⇒ Đường thẳng BC có dạng : 2 x – 3 y + c = 0 ( c ≠ 1 )
Mà điểm B thuộc BC nên : 2. ( – 2 ) – 3 ( – 4 ) + c = 0 ⇔ c = – 8
⇒ phương trình đường thẳng BC : 2 x – 3 y – 8 = 0
Chọn B.
Ví dụ 11: Đường thẳng đi qua A(1; -2), nhận n→ = (1; -2) làm véc tơ pháp tuyến có phương trình là:
A. x – 2y + 1 = 0. B. 2x + y = 0 C. x – 2y – 5 = 0 D. x – 2y + 5 = 0
Lời giải
Gọi ( d ) là đường thẳng đi qua A và nhận n → = ( 1 ; – 2 ) làm VTPT
=> Phương trình đường thẳng ( d ) : 1 ( x – 1 ) – 2 ( y + 2 ) = 0 hay x – 2 y – 5 = 0
Chọn C.
C. Bài tập vận dụng
Câu 1: Viết phương trình tổng quát của đường thẳng d đi qua điểm M( -1; 2) và song song với trục Ox.
A. y + 2 = 0 B. x + 1 = 0 C. x – 1 = 0 D. y – 2 = 0
Câu 2: Cho đường thẳng (a) : 2x+ y- 3=0 và (b) : 3x- 4y+ 1= 0. Lập phương trình đường thẳng d đi qua giao điểm của hai đường thẳng a và b ; nhận vecto n→( 2 ; -3) làm VTPT ?
A. 2 x – 3 y + 6 = 0 B. – 2 x – 3 y + 6 = 0 C. 2 x – 3 y + 1 = 0 D. 2 x + 3 y – 1 = 0
Câu 3: Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A(2; -1), B(4; 5) và C( -3; 2). Lập phương trình đường cao của tam giác ABC kẻ từ B
A. 3 x – 5 y + 1 = 0 B. 3 x + 5 y – 20 = 0 C. 3 x + 5 y – 12 = 0 D. 5 x – 3 y – 5 = 0
Câu 4: Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A(2;-1) ; B( 4;5) và C( -3; 2). Tìm trực tâm tam giác ABC?
A. ( 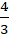
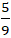
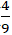
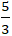
Câu 5: Cho tam giác ABC có A( 2;-1) ; B( 4; 5) và C( -3; 2). Phương trình tổng quát của đường cao AH của tam giác ABC là:
A. 3 x – 7 y + 11 = 0. B. 7 x + 3 y – 11 = 0 C. 3 x – 7 y – 13 = 0. D. 7 x + 3 y + 13 = 0 .
Câu 6: Cho đường thẳng (d): 3x- 2y+ 8= 0. Đường thẳng ∆ đi qua M(3; 1) và song song với (d) có phương trình:
A. 3 x – 2 y – 7 = 0. B. 2 x + 3 y – 9 = 0. C. 2 x – 3 y – 3 = 0. D. 3 x – 2 y + 1 = 0
Câu 7: Cho tam giác ABC có B(2; -3). Gọi I và J lần lượt là trung điểm của AB và AC. Biết đường thẳng IJ có phương trình x- y+ 3= 0. Lập phương trình đường thẳng BC?
A. x + y + 2 = 0 B. x – y – 5 = 0 C. x – y + 6 = 0 D. x – y = 0
Câu 8: Cho tam giác ABC cân tại A có A(3 ; 2). Gọi M là trung điểm của BC và M( -2 ; -4). Lập phương trình đường thẳng BC ?
A. 6 x – 5 y + 13 = 0 B. 5 x – 6 y + 6 = 0 C. 5 x + 6 y + 34 = 0 D. 5 x + 6 y + 1 = 0
Câu 9: Lập phương trình đường thẳng d đi qua điểm M( 2 ; 1) và nhận vecto n→( -2 ; 1) làm VTPT ?
A. 2 x + y – 5 = 0 B. – 2 x + y + 3 = 0 C. 2 x – y – 4 = 0 D. 2 x + y – 1 = 0
Source: http://wp.ftn61.com
Category: Hỏi Đáp
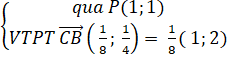



Để lại một bình luận