Các công thức Logarit, phương trình mũ và phương trình Logarit

Công thức Logarit là một nội dung kỹ năng và kiến thức mới và lạ mà học viên sẽ được học trong chương trình toán lớp 12. Đạo hàm logarit là phần kiến thức và kỹ năng sẽ có trong đề thi Đại học nên những bạn học viên cần đặc biệt quan trọng chú ý quan tâm phần kiến thức và kỹ năng quan trọng này. Nếu bạn đang gặp khó khăn vất vả trong việc ghi nhớ những công thức logarit cũng như giải phương trình logarit thì trong bài viết này, chúng tôi sẽ tổng hợp và mách bạn cách ghi nhớ bảng công thức đạo hàm logarit nhanh nhất nhé !

Xem thêm

• Định lý Viet và ứng dụng giải những dạng toán cơ bản

Logarit là gì ?

Logarit viết tắt là Log hay thường được gọi là đạo hàm ln, là phép toán nghịch đảo của lũy thừa. Theo đó, logarit của một số ít là số mũ của cơ số được nâng lên lũy thừa để tạo ra số khác. Hiểu đơn thuần, logarit là một phép nhân với số lần lặp đi lặp lại .
Định nghĩa về logarit được bộc lộ qua biểu thức sau :

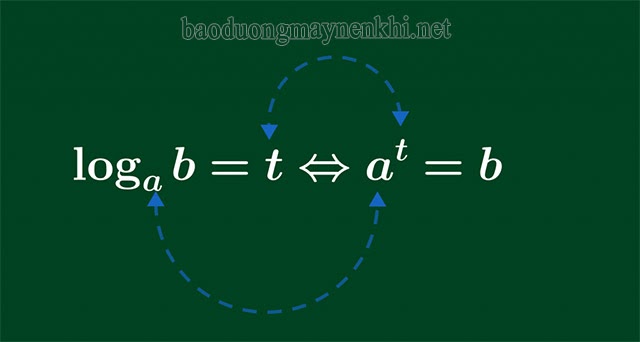
Chúng ta cùng xét một ví dụ đơn cử đơn thuần sau. Nếu ta lấy lũy thừa 3 của 2 thì ta có 2 ³ = 8. Điều đó có nghĩa là nếu ta lấy logarit cơ số 2 của 8 thì ta sẽ được tác dụng là 3 .
Nếu bạn chưa thể phân biệt được vị trí của a, b, t. Để khắc phục, bạn hãy nhớ “ cơ số vẫn mãi là cơ số ” và tưởng tượng sơ đồ như ảnh trên. Đầu tiên ta thay t bằng logarit cơ số a của b ở đẳng thức bên phải .

Như vậy, phương trình logarit luôn có chữ log. Nếu phương trình có thêm số mũ nghĩa là biến số được nâng lên thành lũy thừa thì đó là phương trình hàm mũ. Số mũ sẽ được đặt sau một số ít :

Tổng quát:

Logarit : Logax = y
Số mũ : ay = x

Các thành phần của công thức Logarit

Ví dụ công thức logarit : log28 = 3
Các thành phần của công thức logarit : Log là viết tắt của logarit. Cơ số là 2. Đối số là 8. Số mũ là 3 .

Tính chất của logarit

Tính chất của logarit giúp bạn giải những phương trình logarit và hàm mũ. Nếu thiếu đi những đặc thù logarit này, bạn sẽ không hề giải được phương trình logarit. Tính chất của logarit chỉ dùng được khi cơ số và đối số của logarit dương ( điều kiện kèm theo cơ số a # 1 hoặc 0 ) .

Bảng tóm tắt hàng loạt những công thức Logarit

Quy tắc tính Logarit

Logarit của một tích

Công thức logarit của một tích như sau : logα ( ab ) = logαb + logαc ; Điều kiện : a, b, c đều là số dương với a # 1 .
Đây là logarit hai số a và b triển khai theo phép nhân trải qua phép cộng logarit sinh ra vào thế kỷ 17. Sử dụng bảng logarit, ta sẽ đưa logarit về cơ số a = 10 là logarit thập phân sẽ thuận tiện tra bảng, thống kê giám sát hơn. Logarit tự nhiên với hằng số e là cơ số ( khoảng chừng bằng 2,718 ) được vận dụng thuận tiện trong toán học. Logarit nhị phân có cơ số 2 được dùng trong khoa học máy tính .
Nếu muốn thu nhỏ khoanh vùng phạm vi những đại lượng, bạn dùng thang logarit .

Logarit của lũy thừa

Ta có công thức logarit như sau : logabα = α logab ; điều kiện kèm theo với mọi số α, a và b là số dương với a # 1 .

Công thức logarit và cách giải nhanh

Về công thức đạo hàm logarit và cách giải bài tập logarit nhanh, bạn sẽ cần chăm sóc đến logarit hàm số lũy thừa, hàm số logarit và công thức mũ logarit. Công thức logarit tuy không khó nhưng dễ nhầm lẫn và thiếu sót điều kiện kèm theo logarit khi làm nhiều dạng toán khác nhau. Mẹo để bạn làm tốt bài tập logarit là học kỹ triết lý, hiểu chắc như đinh yếu tố sẽ giúp bạn tránh được điều này. Đồng thời ghi nhớ công thức logarit nhanh bằng cách giải bài tập logarit lặp đi lặp lại nhiều lần và thử những dạng toán khác nhau .

Cách sử dụng bảng đạo hàm Logarit

Với bảng đạo hàm logarit, bạn sẽ đo lường và thống kê nhanh hơn rất nhiều so với việc sử dụng máy tính, đặc biệt quan trọng khi muốn giám sát nhanh hoặc nhân số lớn, sử dụng bảng logarit thuận tiện hơn cả .

Cách tìm logarit nhanh

Để tìm logarit nhanh, bạn cần chú ý quan tâm những điều sau đây :

• Chọn bảng đúng : Hầu hết những bảng đạo hàm logarit là cho logarit cơ số 10 được gọi là logarit thập phân .
• Tìm ô đúng : Giá trị của ô chính tại những giao điểm của hàng dọc và hàng ngang .
• Tìm số đúng mực nhất bằng cách dùng những cột nhỏ hơn ở phía bên phải của bảng ( Cách này sử dụng trong trường hợp số có 4 hoặc nhiều hơn ) .
• Tìm tiền tố trước 1 số ít thập phân : Bảng đạo hàm của log cho bạn biết tiền tố trước 1 số ít thập phân. Phần sau dấu phẩy tên là mantissa .
• Tìm phần nguyên. Cách này dễ tìm nhất so với hàm log cơ số 10. Bạn tìm bằng cách đếm số còn lại của số thập phân và trừ đi một chữ số .

Cách tìm logarit nâng cao

Muốn giải những phương trình mũ và logarit nâng cao, bạn cần chú ý quan tâm những điều sau đây :

• Hiểu hàm số logarit là gì ? Ví dụ, 102 là 100, 103 là 1000. Như vậy số mũ 2, 3 là logarit cơ số 10 của 100 và 1000. Mỗi bảng công thức log chỉ hoàn toàn có thể sử dụng được với một cơ số nhất định. Cho đến nay, loại bảng công thức log phổ cập nhất là logarit cơ số 10, còn gọi là logarit đại trà phổ thông .
• Xác định đặc thù của số mà bạn muốn tìm logarit
• Khi tra bảng đạo hàm logarit, bạn nên cẩn trọng dùng ngón tay tra hàng dọc ngoài cùng bên trái để tính logarit trong bảng. Sau đó, bạn trượt ngón tay để tra hiệu quả ở điểm giao giữa hàng dọc và hàng ngang .

• Nếu bảng logarit có thêm bảng phụ nhỏ dùng để tính toán phép tính lớn hoặc để tìm giá trị chính xác hơn, bạn trượt tay đến cột được đánh dấu bằng chữ số tiếp theo của số bạn đang tìm kiếm trong bảng đó 

  Xem thêm: Làm Thế Nào Để Win 7 Chạy Nhanh Hơn

• Thêm những số được tìm thấy trong 2 bước trước đấy với nhau .
• Thêm đặc tính : Khi tra điểm giao của hai hàng ra số cần tìm, bạn thêm đặc tính với mantissa ở trên để có được hiệu quả tính logarit của mình .

Mẹo nhớ nhanh những công thức tính Logarit

Để nắm chắc kỹ năng và kiến thức tương quan đến đạo hàm ln, những bạn hoàn toàn có thể vận dụng 6 chiêu thức sau đây :

• Nắm vững kiến thức và kỹ năng nền tảng về Logarit, tập xác lập của hàm số logarit, bảng tổng hợp những công thức Logarit cơ bản
• Vì số lượng công thức log nhiều như vậy nên những bạn hoàn toàn có thể sử dụng giấy nhớ để ghi lại những công thức và dán tại những vị trí trong nhà mà mình hay quan sát, đặc biệt quan trọng là bàn học .
• Một cách thông dụng hơn là rèn luyện, giải thật nhiều những bài tập logarit cơ bản và nâng cao để nắm chắc kiến thức và kỹ năng hơn .
• Học nhóm và tìm hiểu thêm quan điểm thầy cô, bạn hữu sẽ giúp bạn hiểu sâu hơn về những kỹ năng và kiến thức cơ bản và nâng cao của công thức đạo hàm logarit
• Tham khảo những video, bài giảng qua những trang mạng tương quan đến đạo hàm ln

Ứng dụng công thức logarit giải bài tập

Công thức logarit vận dụng vào nhiều dạng bài tập logarit khác nhau như tìm điều kiện kèm theo xác lập của biểu thức chứa logarit, tập xác lập của log, biến hóa đạo hàm của log, so sánh biểu thức logarit. Các bài tập này đều là nền tảng cho phần đồ thị hàm logarit mà tất cả chúng ta sẽ được khám phá ở những bài học kinh nghiệm tiếp theo .

Dạng 1 : Tìm điều kiện kèm theo xác lập của biểu thức logarit

Ghi nhớ

Chú ý rằng : Khi giải bất phương trình An > 0 cần nhớ :

• n là số tự nhiên lẻ thì An > 0 ⇔ A > 0 .
• n là số tự nhiên chẵn thì An > 0 ⇔ A ≠ 0 .

Dạng 2 : Rút gọn và tính giá trị biểu thức logarit

Dạng 3 : Biểu diễn logarit theo những logarit đã biết

Ghi nhớ
Để xử lý bài toán màn biểu diễn hàm logarit theo những logarit đã biết, tất cả chúng ta hoàn toàn có thể sử dụng một trong hai cách :

• Cách 1 : Sử dụng những đặc thù của logarit .

• Cách 2 : Sử dụng MTCT .

Thủ thuật dùng máy tính Casio giải phương trình logarit

Phương pháp thông số hóa biến

• Bước 1 : Dựa vào hệ thức điều kiện kèm theo buộc của đề bài chọn giá trị thích hợp cho biến
• Bước 2 : Tính những giá trị tương quan đến biến rồi gắn vào A, B, C nếu những giá trị tính được lẻ
• Bước 3 : Quan sát 4 đáp án và chọn đáp án đúng chuẩn

Phương pháp casio

Tính giá trị của a = log23. Vì giá trị của a là một số lẻ, vậy ta lưu a vào A

Tính giá trị của b = log53 và lưu vào B

Kết quả hiển thị của máy tính Casio là 1 giá trị khác 0 vậy đáp án A sai

3. Phương pháp tự luận

Các bạn học sinh hãy sử dụng các công thức Logarit mà chúng tôi đã thống kê theo bảng rất dễ thuộc và ghi nhớ để vận dụng vào giải các bài tập, phương trình logarit thật thuần thục nhé!

Source: http://wp.ftn61.com
Category: Thủ Thuật