Bảng nguyên hàm và các phương pháp tìm nguyên hàm từ A – Z

Trong bài trước chúng tôi đã chia sẻ tới các bạn kiến thức về công thức lượng giác, công thức đạo hàm. Hôm nay, chúng tôi tiếp tục giới thiệu tới các bạn kiến thức về bảng nguyên hàm, công thức nguyên hàm hay các phương pháp tìm nguyên hàm là một trong những dạng bài tập thường gặp ở các đề thì tốt nghiệp phổ thông và đại học hiện nay. Mời các bạn cùng tham khảo nhé

Công thức nguyên hàm cơ bản thường gặp

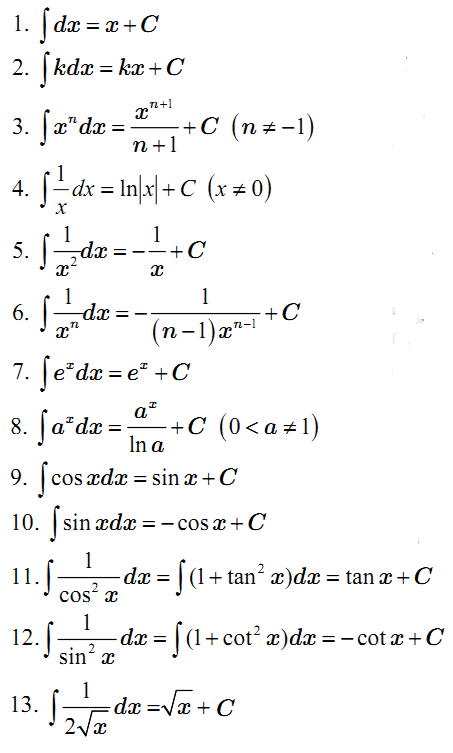
Công thức nguyên hàm mở rộng (a ≠ 0)

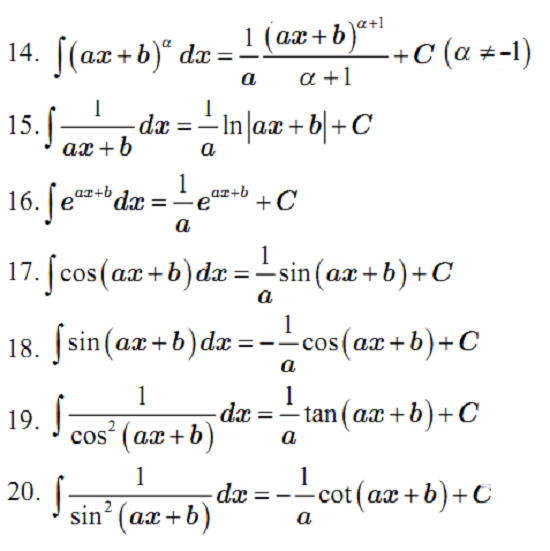
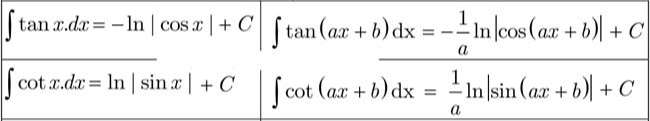
Thực ra, ta đã vận dụng đặc thù sau đây : Nếu F ( x ) là một nguyên hàm của f ( x ) thì :

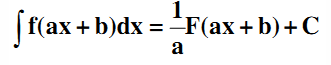
Bảng nguyên hàm nâng cao (a ≠ 0)

Bảng nguyên hàm hàm hợp

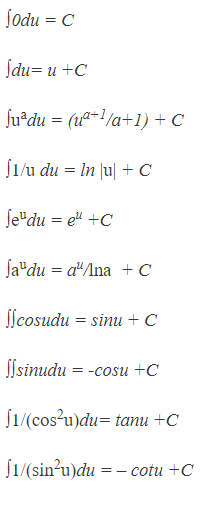
Bảng nguyên hàm đạo hàm

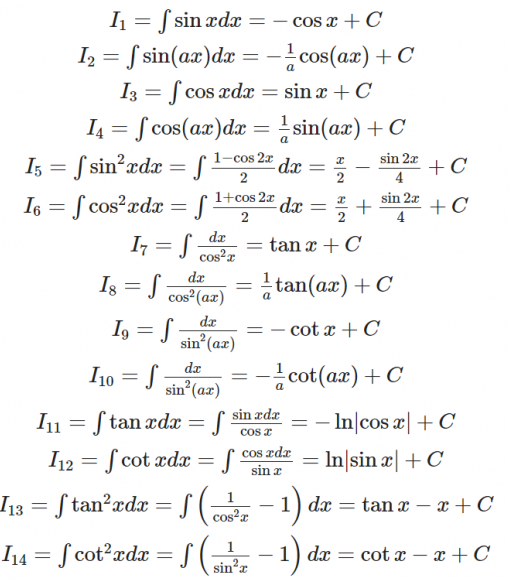
Các phương pháp tìm nguyên hàm

1. Phương pháp đổi biến

1.1. Đổi biến dạng 1

a. Định nghĩa.

Cho hàm số u = u ( x ) có đạo hàm liên tục trên K và hàm số y = f ( u ) liên tục sao cho f [ u ( x ) ] xác lập trên K. Khi đó, nếu F là một nguyên hàm của f, tức là : ∫ f ( u ) du = F ( u ) + C thì :
∫ f [ u ( x ) ] u ‘ ( x ) dx = F [ u ( x ) ] + C

b. Phương pháp giải

• Bước 1: Chọn t = φ(x). Trong đó φ(x) là hàm số mà ta chọn thích hợp.
• Bước 2: Tính vi phân hai vế: dt = φ'(t)dt.
• Bước 3: Biểu thị: f(x)dx = f[φ(t)]φ'(t)dt = g(t)dt.
• Bước 4: Khi đó: I = ∫ f(x)dx = ∫g(t)dt = G(t) + C

1.2. Phương pháp đổi biến loại 2

a. Định nghĩa:

Cho hàm số f ( x ) liên tục trên K ; x = φ ( t ) là một hàm số xác lập, liên tục trên K và có đạo hàm là φ ‘ ( t ). Khi đó, ta có :
∫ f ( x ) dx = ∫ f [ φ ( t ) ]. φ ‘ ( t ) dt

b. Phương pháp chung

• Bước 1: Chọn x = φ( t), trong đó φ(t) là hàm số mà ta chọn thích hợp.
• Bước 2: Lấy vi phân hai vế: dx = φ'(t)dt.
• Bước 3: Biến đổi: f(x)dx = f[φ(t)]φ'(t)dt = g(t)dt.
• Bước 4: Khi đó tính: ∫ f(x)dx = ∫g(t)dt = G(t) + C.

c. Các dấu hiệu đổi biến thường gặp

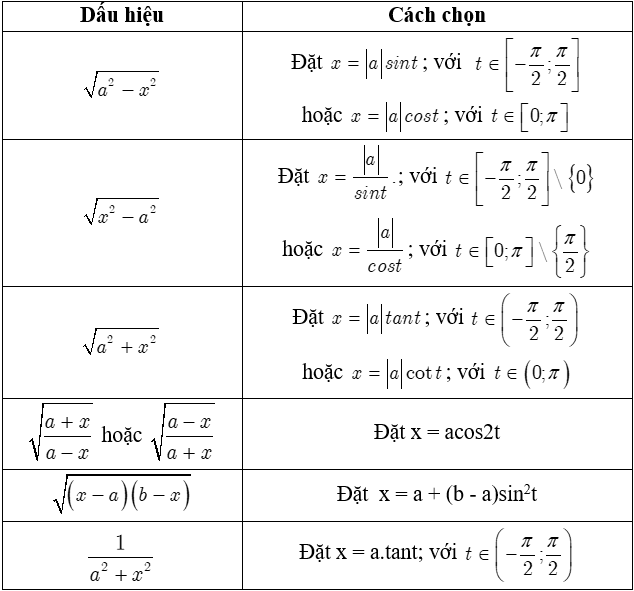
2. Phương pháp nguyên hàm từng phần

a. Định lí

Nếu u ( x ), v ( x ) là hai hàm số có đạo hàm liên tục trên K :
∫ u ( x ). v ‘ ( x ) dx = u ( x ). v ( x ) – ∫ v ( x ). u ‘ ( x ) dx

Hay ∫udv = uv – ∫vdu

( với du = u ‘ ( x ) dx, dv = v ‘ ( x ) dx )

b. Phương pháp chung

• Bước 1: Ta biến đổi tích phân ban đầu về dạng: I = ∫ f(x)dx = ∫ f1(x).f2(x)dx
• Bước 2: Đặt
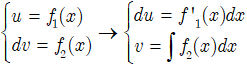
• Bước 3: Khi đó: ∫u.dv = u.v – ∫v.du

c. Các dạng thường gặp

Dạng 1

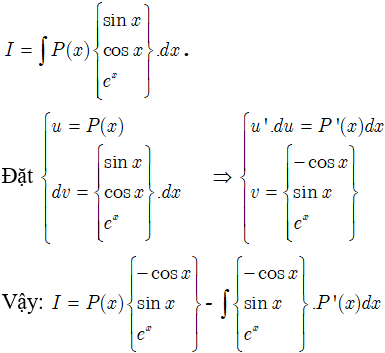
Dạng 2 :

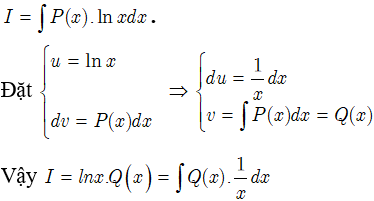
Dạng 3 :

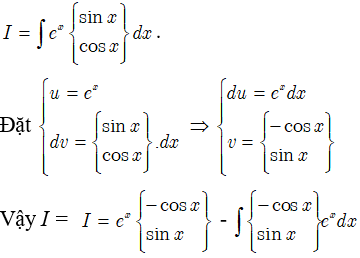
Bên trên chính là hàng loạt bảng nguyên hàm và giải pháp tìm nguyên hàm mà chúng tôi vừa chia sẽ cụ thể sẽ giúp những bạn mạng lưới hệ thống lại kỹ năng và kiến thức của mình nhé

Đánh giá bài viết

Source: http://wp.ftn61.com
Category: Thủ Thuật