Tóm tắt nội dung bài viết
Điều Kiện Phương Trình Mũ Logarit Chứa Tham Số M, Tập Xác Định Của Hàm Số Mũ Lũy Thừa Lôgarit
Tập xác định của hàm số mũ, lũy thừa, logarit tìm như thế nào?. Bài viết dưới đây tôi sẽ hướng dẫn các bạn các tìm tập xác định của ba loại hàm số kể trên. Hãy cùng theo dõi nhé!
I. TẬP XÁC ĐỊNH CỦA HÀM SỐ MŨ
Với hàm số mũ
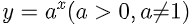
thì không có điều kiện. Nghĩa là tập xác định của nó là R.
Bạn đang đọc: Điều Kiện Phương Trình Mũ Logarit Chứa Tham Số M, Tập Xác Định Của Hàm Số Mũ Lũy Thừa Lôgarit
Đang xem : điều kiện phương trình mũ
Vì vậy khi tất cả chúng ta gặp bài toán tìm tập xác lập của hàm số
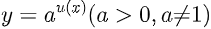
Thì ta chỉ viết điều kiện để cho u ( x ) xác lập .
Ví dụ:
Tìm tập xác lập của hàm số
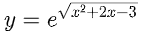
Lời giải:
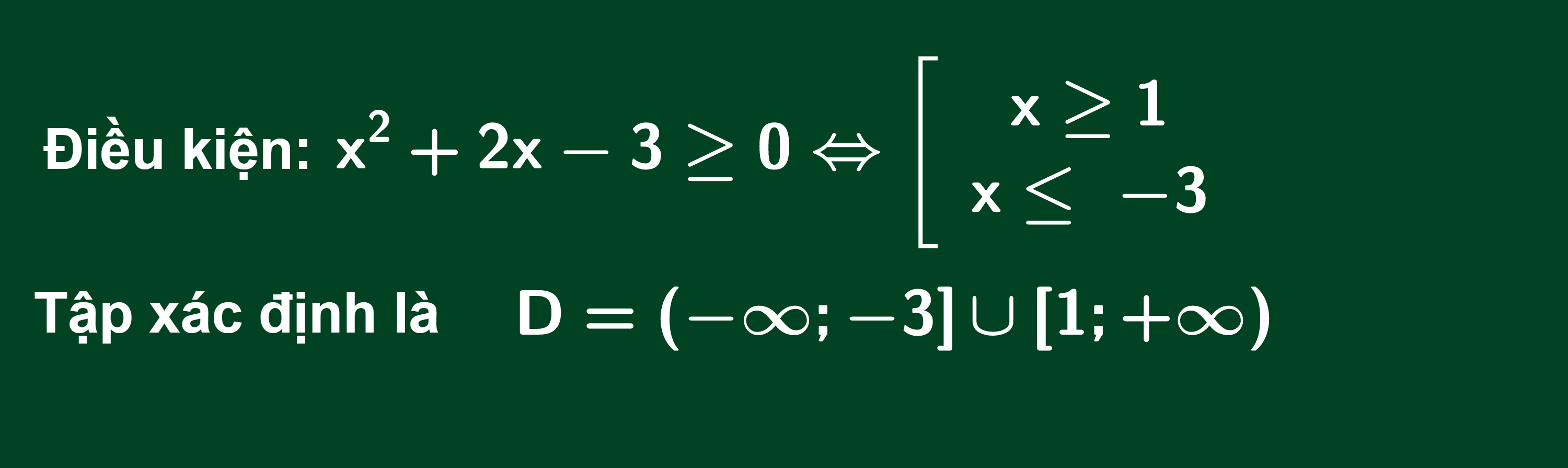
Bộ đề thi Online các dạng có giải chi tiết: Hàm số lũy thừa – Mũ – Logarit
II. TẬP XÁC ĐỊNH CỦA HÀM SỐ LOGARIT
Hàm số logarit
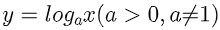
có tập xác lập là ( 0 ; + ∞ ) .
Xem thêm : đề cương luận văn thạc sĩ văn hóa truyền thống
Vì vậy với bài toán tìm tập xác lập của hàm số
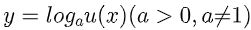
thì điều kiện xác định là u(x)>0 và u(x) xác định.
Xem thêm : Share Khóa Học Mát Xa Cho Chồng, Khóa Học Nghệ Thuật Massage Cho Chồng Yêu
Ví dụ:
Tìm tập xác lập của hàm số sau
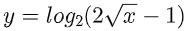
Lời giải:
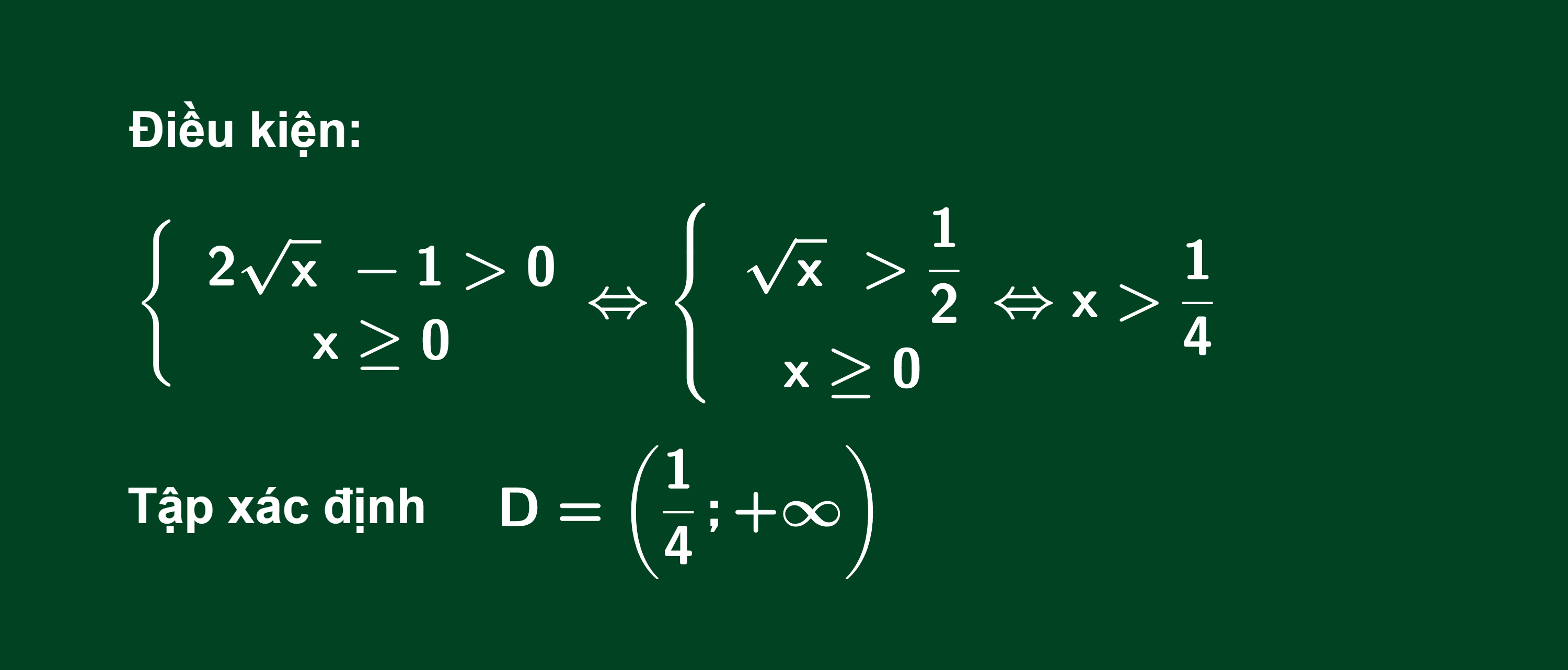
II. TẬP XÁC ĐỊNH CỦA HÀM SỐ LŨY THỪA
Theo quy ước của sách giáo khoa giải tích 12 thì hàm số lũy thừa có tập xác lập nhờ vào vào lũy thừa. Có tổng thể 3 trường hợp khác nhau về lũy thừa ảnh hưởng tác động đến tập xác lập là : Lũy thừa với số mũ nguyên dương ; Lũy thừa số mũ nguyên không dương ; Lũy thừa số mũ không nguyên .
Ở đây tất cả chúng ta xét hàm số lũy thừa dạng
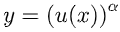
Ngoài điều kiện để u ( x ) xác lập. Chúng ta xét những trường hợp như đã nói ở trên theo sơ đồ sau :
Bộ đề thi Online các dạng có giải chi tiết: Hàm số lũy thừa – Mũ – Logarit
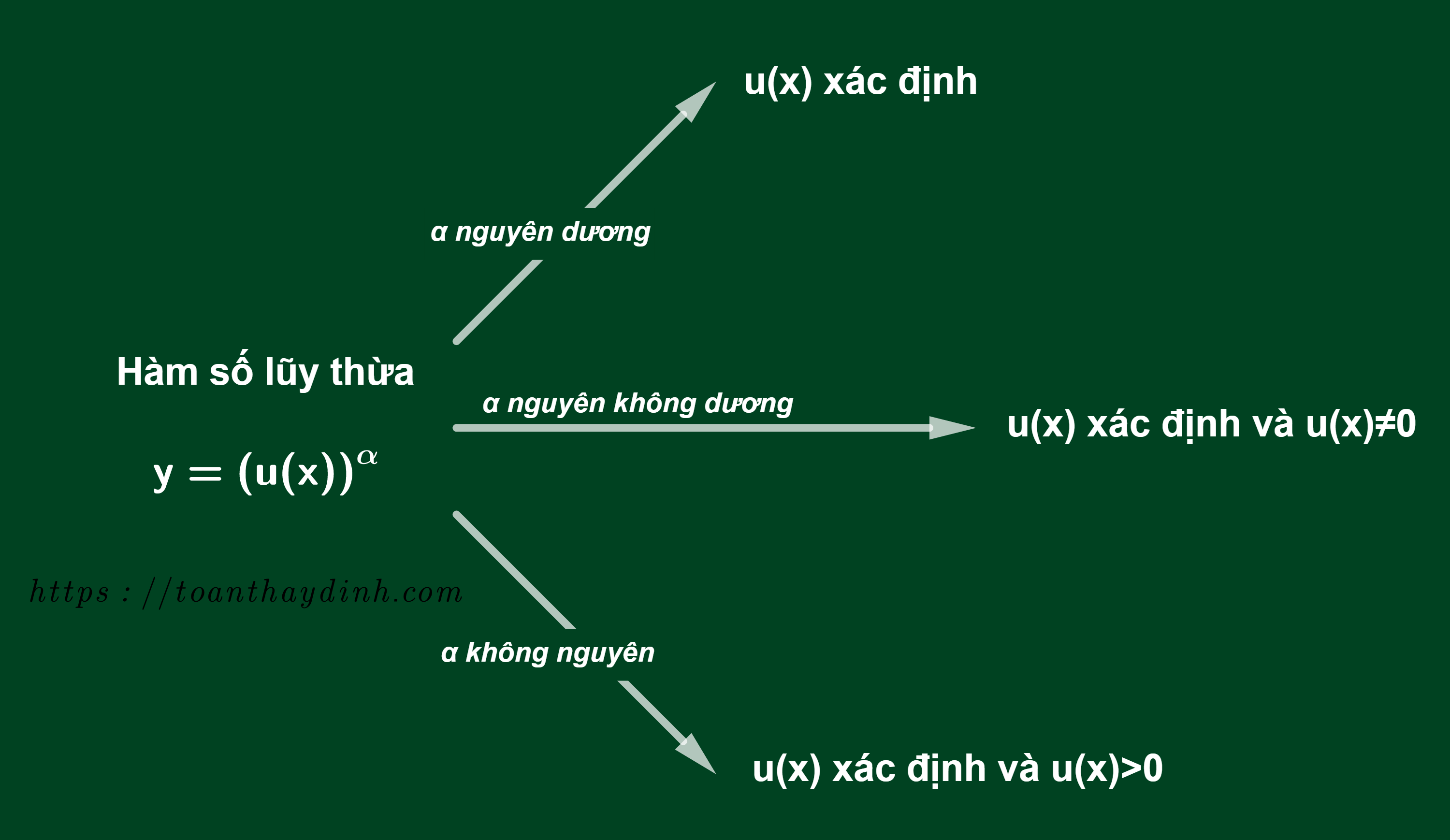
Cách tìm tập xác định hàm số lũy thừa
Ví dụ:
Tìm tập xác lập của hàm số
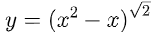
Bộ đề thi Online các dạng có giải chi tiết: Hàm số lũy thừa – Mũ – Logarit
Lời giải:

Trên đây là cách tìm tập xác lập của 3 loại hàm số : Lũy thừa ; Mũ ; Logarit. Mà lingocard.vn gửi tới những bạn. Hãy ghi nhớ để vận dụng vào những bài toán mà những bạn gặp phải. Chúc những bạn thành công xuất sắc !
Xem thêm bài viết thuộc chuyên mục: Phương trình
Điều hướng bài viết
Source: http://wp.ftn61.com
Category: Hỏi Đáp



Để lại một bình luận