Lý thuyết Giải hệ phương trình bằng phương pháp thế.>

1. Các kiến thức cần nhớ

Quy tắc thế

Phương pháp thế là một trong những cách biến hóa tương tự một hệ phương trình, ta sử dụng quy tắc thế, gồm có hai bước, sau đây :

Bước 1. Từ một phương trình của hệ phương trình đã cho (coi là phương trình thứ nhất), ta biểu diễn một ẩn theo ẩn kia rồi thế vào phương trình thứ hai để được một phương trình mới (chỉ còn một ẩn).

Bước 2. Dùng phương trình mới ấy để thay thế cho phương trình thứ hai trong hệ phương trình và giữ nguyên phương trình thứ nhất, ta được hệ phương trình mới tương đương với hệ phương trình đã cho.

Chú ý:

+ Nếu thấy Open phương trình có những thông số của hai ẩn đểu bằng 0 thì hệ phương trình đã cho hoàn toàn có thể có vô số nghiệm hoặc vô nghiệm .

2. Các dạng toán thường gặp

Dạng 1: Giải hệ phương trình bằng phương pháp thế

Phương pháp:

Căn cứ vào quy tắc thế, để giải hệ phương trình bậc nhất hai ẩn bằng phương pháp thế, ta làm như sau :

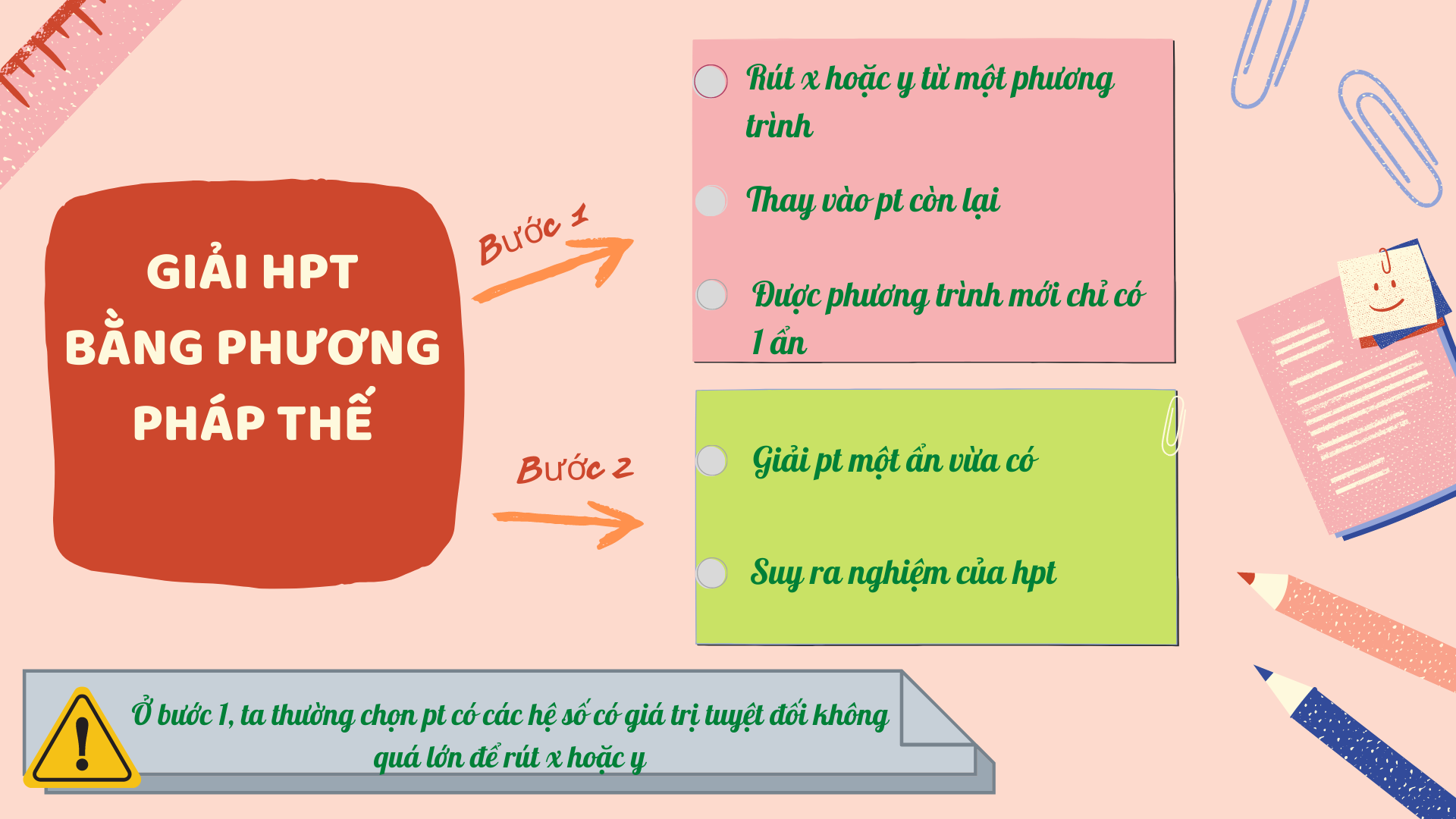
Bước 1. Rút $x$ hoặc $y$ từ một phương trình của hệ phương trình, thay vào phương trình còn lại, ta được phương trình mới chỉ còn một ẩn.

Bước 2. Giải phương trình một ẩn vừa có, rồi từ đó suy ra nghiệm của hệ phương trình đã cho.

Để giải thuật được đơn thuần, ta thường chọn phương trình có những thông số có giá trị tuyệt đối không quá lớn ( thường là USD 1 USD hoặc USD – 1 USD ) và rút $ x USD hoặc USD y $ có thông số có giá trị tuyệt đối nhỏ hơn qua ẩn còn lại .

Dạng 2: Giải hệ phương trình quy về hệ phương trình bậc nhất hai ẩn

Phương pháp:

Bước 1. Biến đổi hệ phương trình đã cho về hệ phương trình bậc nhất hai ẩn.

Bước 2. Giải hệ phương trình bậc nhất hai ẩn bằng phương pháp thế như ở Dạng 1.

Dạng 3: Giải hệ phương trình bằng cách đặt ẩn phụ

Phương pháp:

Bước 1. Đặt ẩn phụ cho các biểu thức chung trong các phương trình của hệ phương trình đã cho để thu được hệ phương trình bậc nhất hai ẩn mới.

Bước 2. Giải hệ phương trình bậc nhất hai ẩn bằng phương pháp thế như ở Dạng 1, ta tìm được nghiệm của hệ phương trình đã cho.

Dạng 4: Tìm điều kiện của tham số để hệ phương trình thỏa mãn điều kiện cho trước.

Phương pháp:

Một số kiến thức và kỹ năng thường sử dụng

+) Hệ phương trình bậc nhất hai ẩn $\left\{ \begin{array}{l}ax + by = c\\a’x + b’y = c’\end{array} \right.$có nghiệm $\left( {{x_0};{y_0}} \right) \Leftrightarrow \left\{ \begin{array}{l}a{x_0} + b{y_0} = c\\a'{x_0} + b'{y_0} = c’\end{array} \right..$

+ ) Đường thẳng USD d : ax + by = c USD đi qua điểm USD M \ left ( { { x_0 } ; { y_0 } } \ right ) $ $ \ Leftrightarrow a { x_0 } + b { y_0 } = c. $

Source: http://wp.ftn61.com
Category: Hỏi Đáp