Trong nội dung chương trình Đại số lớp 9, các em sẽ được tiếp xúc với hệ hai phương trình bậc nhất hai ẩn. Nó là bài học cần thiết để các em áp dụng trong các bài học về giải phương trình. Bài viết hôm nay, Toppy sẽ giúp các em nắm được khái niệm, hiểu được tập hợp nghiệm và quan trọng hơn là có thể áp dụng giải các bài tập thường gặp nhất.
Tóm tắt nội dung bài viết
Khái niệm về hệ hai phương trình bậc nhất hai ẩn
Hệ hai phương trình bậc nhất hai ẩn là hệ phương trình có dạng:
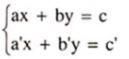
Trong đó, ax+by=c và a’x+b’y=c là phương trình bậc nhất hai ẩn. Để hiểu phương trình bậc nhất 2 ẩn là gì, các em cần nhớ lại kiến thức của bài học trước. Nó dạng phương trình có dạng phương trình có dạng ax + by = c, trong đó a,b,c là những số cho trước a≠0 hoặc
b ≠ 0 .
Trong hệ hai phương trình hai ẩn này, nếu cả hai phương trình thuộc hệ có nghiệm chung thì lúc này nghiệm chung tìm được sẽ là nghiệm của hệ phương trình. Tuy nhiên, những em cũng sẽ gặp trường hợp chẳng tìm được nghiệm nào của phương trình cả. Lúc này, tất cả chúng ta nói hệ phương trình này vô nghiệm. Nếu hệ hai phương trình có cùng tập hợp nghiệm thì sẽ có hệ phương trình cùng tập hợp nghiệm .
Khi đi giải hệ phương trình tức là tất cả chúng ta đang đi tìm nghiệm của hệ phương trình đó. Thế nên khi gặp bài giải hệ phương trình thì tức là đang nhu yếu những em đi tìm nghiệm của hệ phương trình nhé .
Minh họa hình học tập nghiệm của hệ 2 phương trình bậc nhất 2 ẩn
Tập nghiệm của hệ phương trình bậc nhất hai ẩn sẽ được biểu diễn bởi các tập hợp điểm chung của hai đường thẳng sau: ax+by=c (d) và a’x+b’y=c (d’).
Chúng ta có 3 trường hợp xảy ra, gồm :
Trường hợp 1 : d ∩ d ’ = A ( x0, y0 ) tương tự hệ phương trình có nghiệm duy nhất ( x0 ; y0 )
Trường hợp 2 : d / / d ’ thì hệ phương trình vô nghiệm và ngược lại
Trường hợp 3 : d = d ’ thì hệ phương trình có vô số nghiệm và ngược lại .

Cách giải phương trình bậc nhất hai ẩn
Hệ phương trình bậc nhất hai ẩn sẽ được giải bằng hai phương pháp, cũng giống như hệ bất phương trình bậc nhất hai ẩn. Trước tiên là giải hệ phương trình bậc nhất hai ẩn bằng phương pháp cộng đại số, sau đó là phương pháp thế.
Giải hệ phương trình bậc nhất 2 ẩn bằng phương pháp cộng đại số
Phương pháp thế là phương pháp đầu tiên được thực hiện. Ở phương pháp này, quy tắc được đưa ra là biến đổi một hệ phương trình thành hệ phương trình tương đương. Để thực hiện được phép biến đổi này, trước tiên, các em cần cộng hay trừ từng vế phương trình của hệ phương trình đã cho để được một hệ phương trình hai ẩn mới. Sau đó, hãy dùng phương trình mới vừa ra được thay thế cho một trong hai phương trình của hệ, nhớ là giữ nguyên phương trình còn lại.
Xem thêm: Bộ Kế hoạch Đầu tư Tiếng Anh là gì?
Quy tắc này cần được thực thi đúng thì những em mới giải được bằng giải pháp cộng đại số đúng. Các em nên thực thi bài toán bằng cách trải qua những bước sau :
- Bước 1 : Nhân những vế của hai phương trình trong hệ phương trình với một số ít thích hợp, sao cho thông số của một ẩn nào đó trong hai phương trình của hệ phương trình bằng nhau hoặc đối nhau
- Bước 2 : Sử dụng quy tắc cộng đại số tất cả chúng ta vừa nêu ở trên để cho ra tác dụng là một hệ phương trình mới, trong đó quan tâm, một phương trình mà thông số của một trong hai ẩn bằng 0 ( tức là phương trình một ẩn, chứ không phải hai ẩn )
- Bước 3 : Lúc này, phương trình đã là phương trình một ẩn rồi, những em vận dụng cách giải của phương trình một ẩn để tìm ra nghiệm đã cho .
Để hiểu hơn cách vận dụng của giải pháp này, những em theo dõi cách giải bài toán bằng ví dụ sau đây .

Giải hệ phương trình bậc nhất 2 ẩn bằng phương pháp thế
Quy tắc mà các em cần phải nhớ khi sử dụng phương pháp thể để giải hệ hai phương trình bậc nhất hai ẩn chính là dùng để biến đổi một hệ phương trình thành một hệ phương trình mới tương đương. Quy tắc này được thể hiện thông qua hai bước. Đầu tiên, với hệ phương trình đã cho, ta cần biểu diễn một ẩn theo ẩn kia rồi thế vào phương trình thứ 2 để tạo ra một phương trình mới (phương trình một ẩn). Sau đó, dùng phương trình mới này thay thế cho phương trình thứ 2 trong hệ.
Như vậy, để giải theo giải pháp thế, cần làm theo cách sau :
- Bước 1 : Sử dụng quy tắc thế để đổi khác phương trình đã cho sang một hệ phương trình mới, trong đó bắt buộc phải Open một phương trình một ẩn .
-
Bước 2: Giải hệ phương trình một ẩn và tìm kiếm nghiệm của hệ phương trình đã cho.
Với cách giải này, những em sẽ tìm ra nghiệm của hệ phương trình một cách nhanh gọn .

Như vậy, các em đã vừa cùng Toppy tìm hiểu xong khái niệm cũng như các phương pháp giải của hệ hai phương trình bậc nhất hai ẩn rồi. Đây là một kiến thức toán quan trọng cần nắm chắc. Hy vọng thông qua bài học, các em dễ dàng làm được các bài tương tự nhé.
Tìm hiểu thêm:
Source: http://wp.ftn61.com
Category: Hỏi Đáp



Để lại một bình luận