Cách giải phương trình lượng giác cơ bản
A. Phương pháp giải & Ví dụ
– Phương trình sinx = a (1)
♦ |a| > 1: phương trình (1) vô nghiệm.
Bạn đang đọc: Cách giải phương trình lượng giác cơ bản
♦ | a | ≤ 1 : gọi α là một cung thỏa mãn nhu cầu sinα = a .
Khi đó phương trình ( 1 ) có những nghiệm là
x = α + k2π, k ∈ Z
và x = π-α + k2π, k ∈ Z .
Nếu α thỏa mãn điều kiện 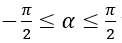
Khi đó những nghiệm của phương trình ( 1 ) là
x = arcsina + k2π, k ∈ Z
và x = π – arcsina + k2π, k ∈ Z .
Các trường hợp đặc biệt:
– Phương trình cosx = a (2)
♦ | a | > 1 : phương trình ( 2 ) vô nghiệm .
♦ | a | ≤ 1 : gọi α là một cung thỏa mãn nhu cầu cosα = a .
Khi đó phương trình ( 2 ) có những nghiệm là
x = α + k2π, k ∈ Z
và x = – α + k2π, k ∈ Z .
Nếu α thỏa mãn nhu cầu điều kiện kèm theo và cosα = a thì ta viết α = arccos a .
Khi đó những nghiệm của phương trình ( 2 ) là
x = arccosa + k2π, k ∈ Z
và x = – arccosa + k2π, k ∈ Z .
Các trường hợp đặc biệt:
– Phương trình tanx = a (3)
Điều kiện:
Nếu α thỏa mãn nhu cầu điều kiện kèm theo và tanα = a thì ta viết α = arctan a .
Khi đó những nghiệm của phương trình ( 3 ) là
x = arctana + kπ, k ∈ Z
– Phương trình cotx = a (4)
Điều kiện : x ≠ kπ, k ∈ Z .
Nếu α thỏa mãn nhu cầu điều kiện kèm theo và cotα = a thì ta viết α = arccot a .
Khi đó những nghiệm của phương trình ( 4 ) là
x = arccota + kπ, k ∈ Z

B. Ví dụ minh họa
Bài 1: Giải các phương trình lượng giác sau:
Bài 2: Giải các phương trình lượng giác sau:
a) sinx = sin(π/6) c) tanx – 1 = 0
b) 2cosx = 1. d) cotx = tan2x.
Bài 3: Giải các phương trình lượng giác sau:
a) cos2 x – sin2x =0.
b) 2sin(2x – 40º) = √3
Đáp án và hướng dẫn giải
Bài 1: Giải các phương trình lượng giác sau:
a) sin(2x+1)=cos(3x+2)
b)
⇔ sin x + 1 = 1 + 4 k
⇔ sin x = 4 k ( k ∈ Z )
Nếu | 4 k | > 1 ⇔ | k | > 1/4 ; phương trình vô nghiệm
Nếu | 4 k | ≤ 1 mà k nguyên ⇒ k = 0. Khi đó :
⇔ sin x = 0 ⇔ x = mπ ( m ∈ Z )
Bài 2: Giải các phương trình lượng giác sau:
a) sinx = sinπ/6
b)
c) tanx=1⇔cosx= π/4+kπ (k ∈ Z)
d) cotx=tan2x
Bài 3: Giải các phương trình lượng giác sau:
a) cos2x-sin2x=0 ⇔cos2x-2 sinx cosx=0
⇔ cos x ( cos x – 2 sin x ) = 0
b) 2 sin(2x-40º )=√3
⇔ sin ( 2 x – 40 º ) = √ 3/2
C. Bài tập vận dụng
Bài 1: Giải các phương trình sau
a) cos2 x – 3cosx + 2 = 0
b) 1/(cos2 x) – 2 = 0.
Lời giải:
Bài 2: Giải các phương trình sau: (√3-1)sinx = 2sin2x.
Lời giải:
Bài 3: Giải các phương trình sau: (√3-1)sinx + (√3+1)cosx = 2√2 sin2x
Lời giải:
Bài 4: Giải các phương trình sau
a) cos(3x + π) = 0
b) cos (π/2 – x) = sin2x
Lời giải:
Bài 5: Giải các phương trình sau
a) sinx.cosx = 1
b) cos2 x – sin2 x + 1 = 0
Lời giải:
Source: http://wp.ftn61.com
Category: Hỏi Đáp
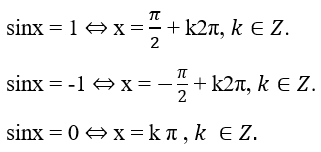
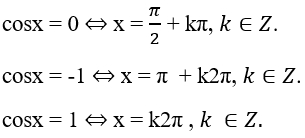
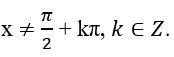
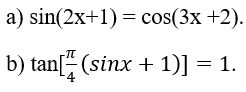
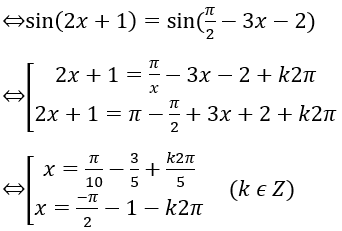
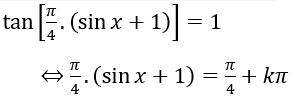
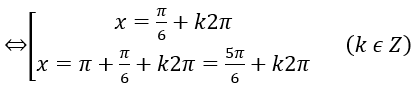
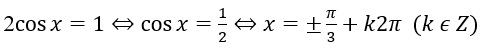
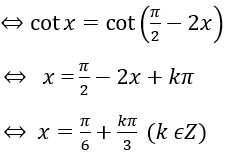
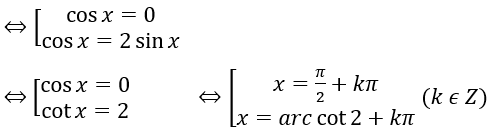
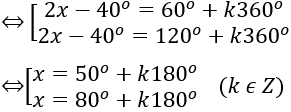
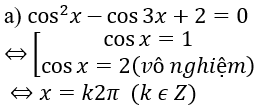
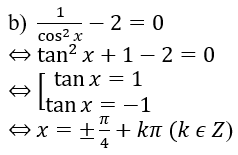
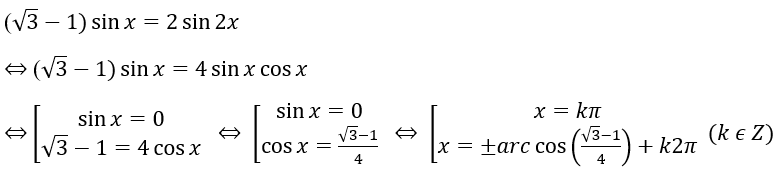
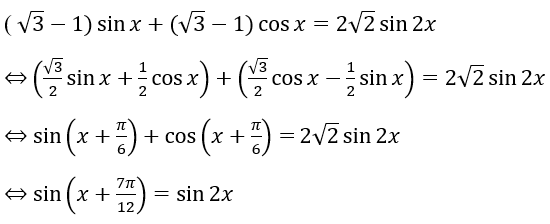
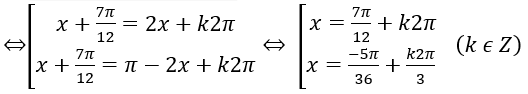
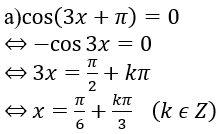
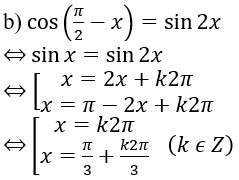
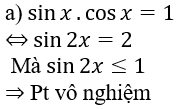
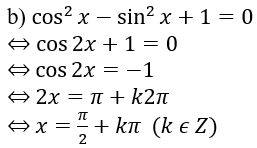



Để lại một bình luận