Tóm tắt nội dung bài viết
Cực trị hàm bậc 4 trùng phương? Lý thuyết, điều kiện và bài tập cực trị của hàm số
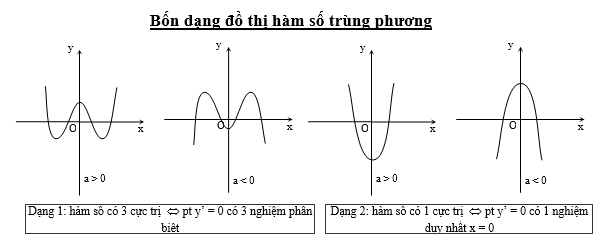
Cực trị hàm bậc 4 trùng phương trong bài viết này của chúng tôi sẽ đem đến cho bạn những nội dung có ích gì ? Cùng xem ngay bài viết dưới đây của chúng tôi để biết được đáp án nhé !
Định nghĩa cực trị hàm số bậc 4
Cho hàm số bậc 4 : y = f(x) = ax^4 + bx^3 + cx^2 + dx + e với a ≠ 0
+ ) Đạo hàm y ′ = 4 ax ^ 3 + 3 bx ^ 2 + 2 cx + d
+ ) Hàm số y = f ( x ) hoàn toàn có thể có một hoặc ba cực trị .
+) Điểm cực trị là điểm mà qua đó thì đạo hàm y′ đổi dấu
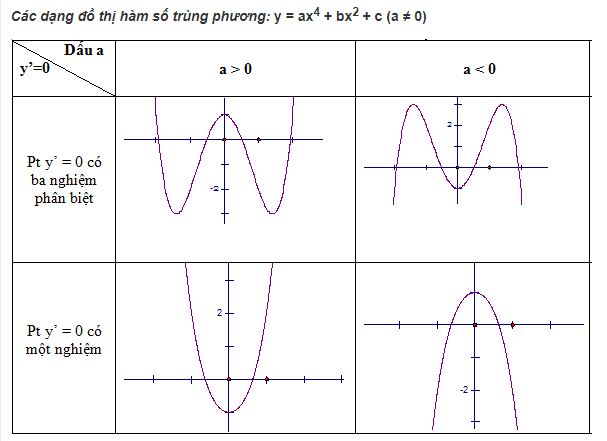
Số điểm cực trị của hàm bậc 4
– Xét đạo hàm y′ = 4ax^3 + 3bx^2 + 2cx + d
+) Nếu y′=0 có đúng 1 nghiệm thì hàm số y= f(x) có đúng 1 cực trị ( có thể là cực đại hoặc cực tiểu ).
+) Nếu y′=0 có 2 nghiệm (gồm 1 nghiệm đơn, 1 nghiệm kép) thì hàm số y= f(x) có đúng 1 cực trị ( có thể là cực đại hoặc cực tiểu ).
+) Nếu y′=0 có 3 nghiệm phân biệt thì hàm số y= f(x) có 3 cực trị ( gồm cả cực đại và cực tiểu ).
Một số điều kiện xét điểm cực tiểu, cực đại của hàm số bậc 4 trùng phương
– Xét hàm số bậc 4 : y = f(x) = ax^4 + bx^2 + c với a ≠ 0
Bài tập cực trị hàm số bậc 4 chứa tham số
Bài tập 1: Chứng minh rằng hàm số f(x) = x^4+mx^3+mx^2+mx+1 không thể đồng thời có cả cực đại và cực tiểu với mọi m ∈ R
– Hướng dẫn giải:
Để chứng tỏ hàm số đã cho không có đồng thời cực lớn lẫn cực tiểu thì ta chứng tỏ hàm số ấy chỉ có duy nhât 1 cực trị với mọi m ∈ R
Xét đạo hàm f′(x) = 4x^3+m(3x^2+2x+1)
Xét phương trình f′(x)=0 ⇔ 4x^3+m(3x^2+2x+1) = 0
⇒ hàm số g ( x ) đồng biến
⇒ phương trình g ( x ) = 0 có đúng 1 nghiệm duy nhất
Như vậy phương trình f ′ ( x ) = 0 có đúng 1 nghiệm duy nhất
⇒ hàm số f ( x ) có duy nhất một điểm cực trị
Bài tập 2: Cho hàm số f(x) = 3mx^4 + (m−2)x^2 + m−1. Tìm m để hàm số đã cho có ba điểm cực trị
– Hướng dẫn giải:
Xét hàm số f(x), ta có f′(x) = 12mx^3 + 2(m-2)x = 0
Để hàm số f ( x ) có 3 điểm cực trị thì a x b < 0
Ta có: 12m x 2(m−2) < 0
⇔ m ∈ ( 0 ; 2 )
Với những nội dung chúng tôi gửi đến bạn, kỳ vọng sẽ đem đến cho bạn những nội dung hữu dụng giúp bạn giải quyết và xử lý những bài toán tương quan đến bậc 4 trùng phương
Cám ơn bạn đã theo dõi bài viết này, hẹn gặp lại bạn ở những bài viết tiếp theo của chúng tôi !
Source: http://wp.ftn61.com
Category: Hỏi Đáp
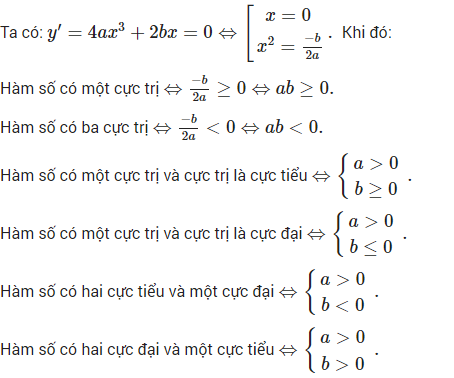
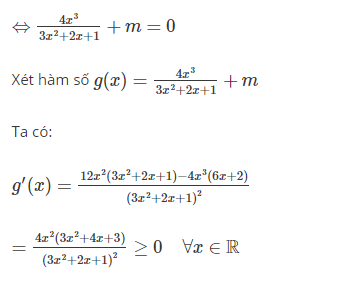


Để lại một bình luận