Phương trình đường elip thuộc chương 3 – toán lớp 10 hình học. Đây là một chuyên đề khá lạ lẫm đối với các em học sinh. Khi các em vừa phải tìm hiểu tọa độ trong mặt phẳng vừa phải học một số công thức được chứng minh sẵn từ hình elip. Ở tài liệu này, chúng tôi xin giới thiệu đến em một số vấn đề: định nghĩa phương trình đường elip, công thức tổng quát, các dạng bài tập đặc trưng liên quan đến tọa độ hình elip.
TẢI XUỐNG PDF ↓
Tóm tắt nội dung bài viết
Lý thuyết phương trình đường elip
Các bài toán về elip chủ yếu qui về việc viết phương trình chính tắc của elip, xác định các phần tử của elip (tâm, đỉnh, tiêu cự, độ dài trục lớn, trục nhỏ, tiêu điểm…). Nhất là xác định phương trình của tiếp tuyến cùng với tọa độ tiếp điểm. Trong mọi trường hợp ta cần nắm vững kiến thức cơ bản sau đây:
- Phương trình chính tắc
- Tiêu cự
- Tiêu điểm
- Trục lớn
- Trục nhỏ
- Đỉnh trên trục lớn
- Đỉnh trên trục nhỏ
- Tâm sai
- Bán kính qua tiêu điểm của M thuộc E
- Đường chuẩn
Các kỹ năng và kiến thức trên được tổng hợp vào bảng sau :

Bài tập phương trình elip cơ bản
Để xử lý tốt những lớp bài toán tương quan tới Elip ( tìm điểm và viết phương trình tắc của elip ) thứ nhất tất cả chúng ta cần nắm được những kiến thức và kỹ năng cơ bản qua sơ đồ sau :
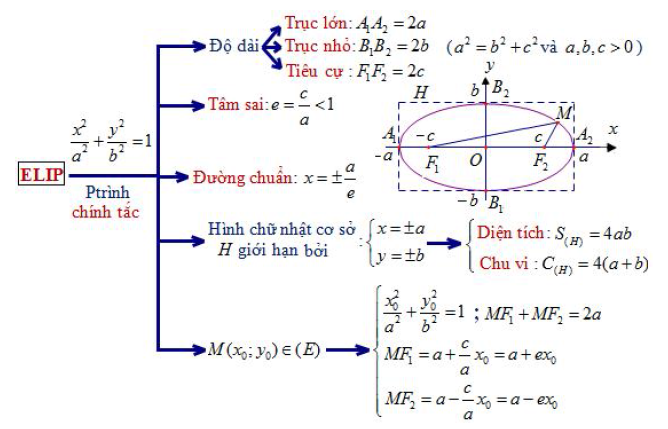
- Lập phương trình chính tắc của một elip khi biết các thành phần đủ để xác đinh elip đó
- Xác định các thành phần của một elip khi biết phương trình chính tắc của elip đó
- Khi gặp bài toán “Tìm điểm thuộc thỏa mãn điều kiện (*) cho trước ” thì về cơ bản ta cần thiết lập được hai dấu “=” mà ở đó dữ kiện điểm thuộc luôn cho ta được một dấu “=” đầu tiên. Các dữ kiện còn lại sẽ giúp ta tìm ra dấu “=” thứ hai. Nếu cần, trong một số bài toán ta có thể tham số hóa điểm thuộc theo một ẩn. Ví như: \[M\in E:\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1\Rightarrow M(a.\sin t;b.\cos t)\]
- Khi gặp bài toán “Viết phương trình chính tắc của elip (E)” cần cắt nghĩa chính xác dữ kiện của bài toán
dựa trên các kiến thức cơ bản liên quan tới elip và tính đối xứng của elip (elip nhận hai trục tọa độ làm hai trục đối xứng và gốc tọa độ làm tâm đối xứng).
Bài tập đề nghị
Ví dụ 1: Trong mặt phẳng tọa độ \[Oxy,\], viết phương trình chính tắc của elip \[(E)\] biết rằng \[(E)\] có tâm sai
bằng \[\frac{\sqrt{5}}{3}\] và hình chữ nhật cơ sở của \[(E)\] có chu vi bằng 20.
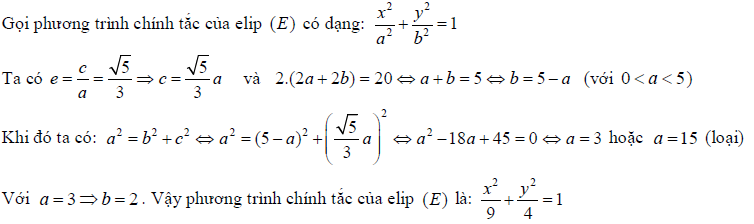
Ví dụ 2: Trong mặt phẳng \[Oxy\] với hệ tọa độ, cho elip có phương trình\[\frac{{{x}^{2}}}{25}+\frac{{{y}^{2}}}{16}=1\]. Tìm điểm M nằm trên elip sao cho \[M{{F}_{1}}=4MF\], trong đó \[{{F}_{1}},{{F}_{2}}\] lần lượt là các tiêu điểm trái, phải của elip.
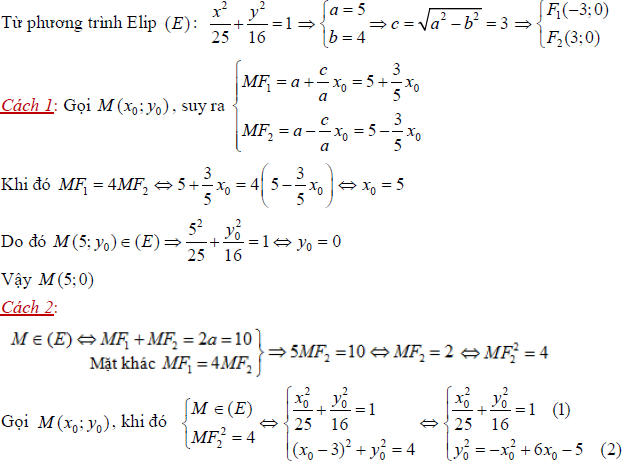
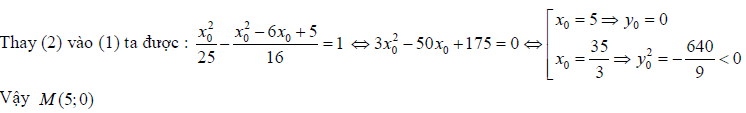
Ví dụ 3: Trong mặt phẳng tọa độ \[Oxy\], cho elip \[(E):\frac{{{x}^{2}}}{4}+{{y}^{2}}=1\] và điểm \[M\left( \frac{2}{3};\frac{2}{3} \right)\]. Viết phương trình đường thẳng \[\Delta \] qua M cắt E tại hai điểm \[A,B\] sao cho \[MA=2MB\].
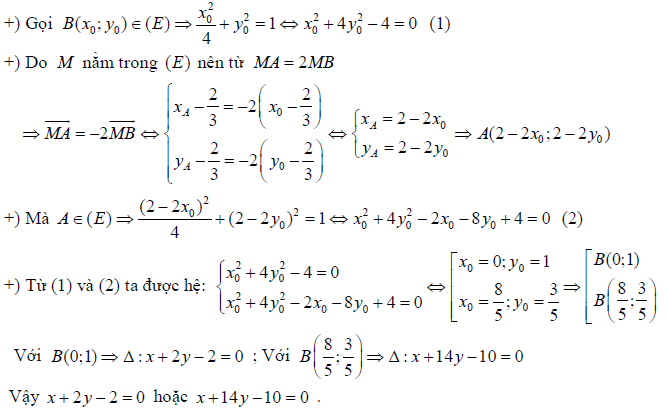
Ví dụ 4: Trong mặt phẳng tọa độ \[Oxy\], cho elip \[(E):\frac{{{x}^{2}}}{8}+\frac{{{y}^{2}}}{4}=1\]. Đường thẳng \[\Delta :x-\sqrt{2}.y=0\] cắt \[(E)\] tại ai điểm \[B,C\]. Tìm tọa độ điểm trên sao cho tam giác có diện tích lớn nhất:
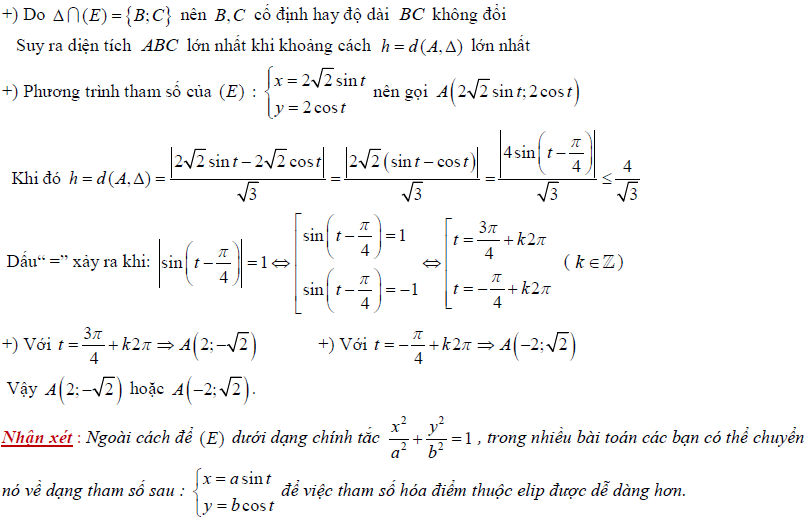
D. BÀI TẬP TỰ LUYỆN CÓ LỜI GIẢI





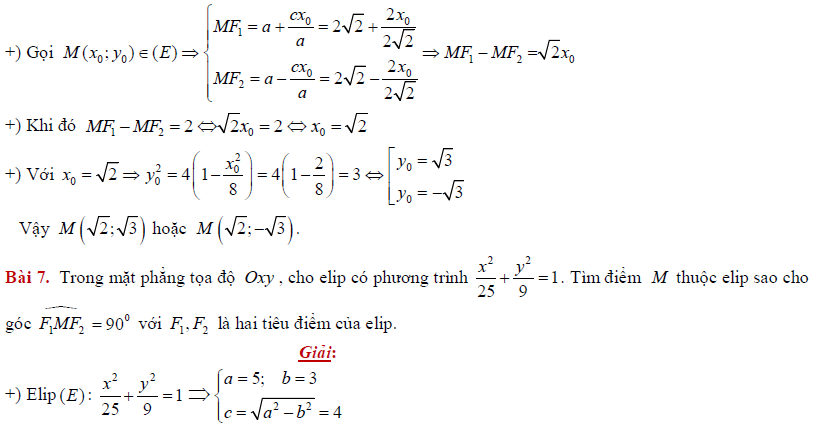




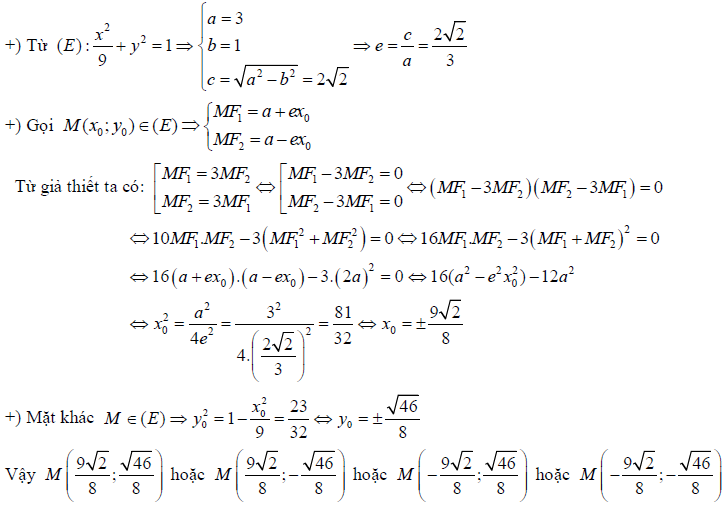




Vậy là chúng ta vừa tìm hiểu xong tất tần tật những điểm lý thuyết cũng như những dạng bài liên quan đến phương trình đường elip. Để xem thêm nhiều tài liệu hay, các em có thể theo dõi website này. Để đạt kết quả cao nhất khi luyện tập, các em có thể tải về và in ra thuận tiện cho việc làm bài tập.
Từ khóa :
- bài tập phương trình đường elip lớp 10 nâng cao
- phương trình hypebol
- phương trình đường tròn
- phương trình tham số của elip
- phương trình elip không chính tắc
- đường thẳng cắt elip tại 2 điểm
- phương trình elip số phức
- cách tính chu vi của elip
Source: http://wp.ftn61.com
Category: Hỏi Đáp


Để lại một bình luận