Viết phương trình đường thẳng đi qua 2 điểm: Lý thuyết và Bài tập

Viết phương trình đường thẳng đi qua 2 điểm là một dạng toán thường gặp trong phần hệ tọa độ mặt phẳng lớp 10. Vậy phương trình đường thẳng là gì? Cách viết phương trình tổng quát đi qua 2 điểm? Cách viết phương trình đường thẳng đi qua 2 điểm cực trị?… Trong nội dung bài viết dưới đây, DINHNGHIA.VN sẽ giúp bạn tổng hợp kiến thức về chủ đề cách viết phương trình đường thẳng đi qua 2 điểm, cùng tìm hiểu nhé!

Tóm tắt nội dung bài viết

Phương trình đường thẳng là gì?
Phương trình tham số của đường thẳng
Phương trình tổng quát của đường thẳng
Cách viết phương trình đường thẳng đi qua 2 điểm
Cách 1: Sử dụng định nghĩa
Cách 2: Sử dụng phương trình tổng quát
Viết phương trình đường thẳng đi qua 2 điểm thuộc trục tọa độ
Viết phương trình đường thẳng đi qua 2 điểm có cùng hoành độ, tung độ
Cách viết phương trình đường thẳng đi qua 2 điểm cực trị

Phương trình đường thẳng là gì?

Phương trình tham số của đường thẳng

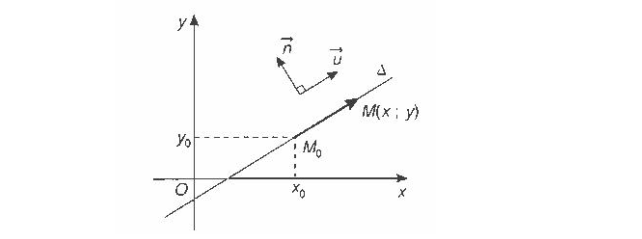
Trong mặt phẳng \ ( Oxy \ ) cho đường thẳng \ ( \ Delta \ ) đi qua điểm \ ( M ( x_0 ; y_0 ) \ ) và nhận \ ( \ vec { u } ( u_1 ; u_2 ) \ ) làm véc tơ chỉ phương. Khi đó phương trình tham số của đường thẳng \ ( \ Delta \ ) là :

\( \left\{\begin{matrix} x = x_0 +u_1t \\ y=y_0 + u_2t \end{matrix}\right. \) với \( t \) là tham số.

Bạn đang đọc: Viết phương trình đường thẳng đi qua 2 điểm: Lý thuyết và Bài tập

Với mỗi giá trị đơn cử của \ ( t \ ) thì ta được tọa độ một điểm nằm trên đường thẳng \ ( \ Delta \ )

Phương trình tổng quát của đường thẳng

Trong mặt phẳng \ ( Oxy \ ) cho đường thẳng \ ( \ Delta \ ) đi qua điểm \ ( M ( x_0 ; y_0 ) \ ) và nhận \ ( \ vec { n } ( a, b ) \ ) làm véc tơ pháp tuyến. Khi đó phương trình tổng quát của đường thẳng \ ( \ Delta \ ) là :
\ ( \ Delta : a ( x-x_0 ) + b ( y-y_0 ) = 0 \ )
\ ( \ Leftrightarrow ax + by + c = 0 \ )

***Chú ý:

Ta biết rằng nếu \ ( \ vec { u } ( u_1 ; u_2 ) \ ) là một véc tơ chỉ phương của đường thẳng \ ( \ Delta \ ) thì \ ( \ vec { u ’ } = ( – u_2 ; u_1 ) \ ) là một véc tơ pháp tuyến của \ ( \ Delta \ ). Vậy khi đó phương trình tổng quát của đường thẳng \ ( \ Delta \ ) là :
\ ( \ Delta : – u_2 x + u_1y + c = 0 \ )
Phương trình tổng quát của đường thẳng hoàn toàn có thể được chuyển về dạng :
\ ( y = ax + b \ ) .
Khi đó \ ( a \ ) được gọi là thông số góc của đường thẳng

Xem Thêm " Cơ Sở Sản Xuất Kinh Doanh Tiếng Anh Là Gì, Đất Cơ Sở Sản Xuất Kinh Doanh

Xem chi tiết >>> Hệ số góc của đường thẳng là gì? Cách tính hệ số góc của đường thẳng

Cách viết phương trình đường thẳng đi qua 2 điểm

Bài toán : Trong mặt phẳng \ ( Oxy \ ) cho hai điểm \ ( A ( x_1 ; y_1 ) \ ) và \ ( B ( x_2 ; y_2 ) \ ). Hãy viết phương trình tổng quát của đường thẳng đi qua hai điểm \ ( A ; B \ )
Để xử lý bài toán này tất cả chúng ta có hai cách làm :

Cách 1: Sử dụng định nghĩa

Bước 1:Xác định véc tơ \ ( \ overrightarrow { AB } = ( x_2-x_1 ; y_2-y_1 ) \ )
Bước 2:Xác định véc tơ pháp tuyến của đường thẳng \ ( AB \ ) : \ ( \ vec { n } = ( y_1-y_2 ; x_2-x_1 ) \ )
Bước 3:Viết phương trình đường thẳng \ ( AB : ( y_1-y_2 ) ( x-x_1 ) + ( x_2-x_1 ) ( y-y_1 ) = 0 \ )

* * * Chú ý : Rút gọn công thức trên ta được
\ ( \ frac { x-x_1 } { x_2-x_1 } = \ frac { y-y_1 } { y_2-y_1 } \ )
Đây chính là công thức nhanh viết phương trình đường thẳng đi qua hai điểm cho trước, thường được sử dụng trong những bài toán trắc nghiệm .

Ví dụ:

Trong mặt phẳng \ ( Oxy \ ) cho hai điểm \ ( A ( 1 ; 2 ) \ ) và \ ( B ( 3 ; – 1 ) \ ). Hãy viết phương trình tổng quát của đường thẳng đi qua hai điểm \ ( A ; B \ )

Cách giải:

Ta có :
\ ( \ vec { AB } = ( 2 ; – 3 ) \ )

\(\Rightarrow \vec{n}=(3;2)\) là vectơ pháp tuyến của đường thẳng \( AB \)

Vậy phương trình đường thẳng \ ( AB \ ) là :
\ ( 3 ( x-1 ) + 2 ( y-2 ) = 0 \ )
\ ( \ Leftrightarrow 3 x + 2 y – 7 = 0 \ )
Cách khác : Áp dụng công thức nhanh, ta có phương trình đường thẳng \ ( AB \ ) là :
\ ( \ frac { x-1 } { 2 } = \ frac { y-2 } { – 3 } \ )
\ ( \ Leftrightarrow 3 x + 2 y – 7 = 0 \ )

Cách 2: Sử dụng phương trình tổng quát

Bước 1:Gọi phương trình đường thẳng \ ( AB \ ) là : \ ( y = ax + b \ )
Bước 2:Lần lượt thay vào tọa độ \ ( A ; B \ ) ta được :
- \ ( \ left \ { \ begin { matrix } y_1 = ax_1 + b \ \ y_2 = ax_2 + b \ end { matrix } \ right. \ )
Bước 3:Giải hệ phương trình trên tìm được \ ( a ; b \ ). Thay vào ta được phương trình đường thẳng \ ( AB \ )

***Chú ý: Cách này chỉ áp dụng với những phương trình đường thẳng dạng \( ax+by+c =0 \) với \(a,b \neq 0\)

Ví dụ:

Trong mặt phẳng \ ( Oxy \ ) cho hai điểm \ ( A ( 3 ; 2 ) \ ) và \ ( B ( – 2 ; 4 ) \ ). Hãy viết phương trình tổng quát của đường thẳng đi qua hai điểm \ ( A ; B \ )

Cách giải:

Gọi phương trình đường thẳng \ ( AB \ ) là : \ ( y = ax + b \ )
Khi đó, thay vào tọa độ của \ ( A, B \ ) ta được :
\ ( \ left \ { \ begin { matrix } 2 = 3 a + b \ \ 4 = – 2 a + b \ end { matrix } \ right. \ )
Giải hệ trên ta được : \ ( \ left \ { \ begin { matrix } a = – \ frac { 2 } { 5 } \ \ b = \ frac { 16 } { 5 } \ end { matrix } \ right. \ )
Thay vào ta được phương trình đường thẳng \ ( AB \ ) :
\ ( y = – \ frac { 2 } { 5 } x + \ frac { 16 } { 5 } \ )
\ ( \ Leftrightarrow 2 x + 5 y – 16 = 0 \ )

Xem Thêm Ai đã giết Binh bộ Thượng thư triều Tây Sơn Ngô Thời Nhiệm?

Xem chi tiết >>> Phương trình đường thẳng trong mặt phẳng

Nhận xét:

Viết phương trình đường thẳng đi qua 2 điểm thuộc trục tọa độ

Nếu hai điểm cùng nằm trên trục \ ( Ox \ Rightarrow \ ) phương trình đường thẳng là phương trình của trục \ ( Ox : y = 0 \ )
Nếu hai điểm cùng nằm trên trục \ ( Oy \ Rightarrow \ ) phương trình đường thẳng là phương trình của trục \ ( Oy : x = 0 \ )
Nếu một điểm nằm trên \ ( Ox \ ) có tọa độ \ ( ( a ; 0 ) \ ) và một điểm nằm trên \ ( Oy \ ) có tọa độ \ ( ( 0 ; b ) \ ) thì phương trình đường thẳng là :
- \ ( \ frac { x } { a } + \ frac { y } { b } = 1 \ )Đây là phương trình đường thẳng theo đoạn chắn.

Ví dụ:

Trong mặt phẳng \ ( Oxy \ ) cho hai điểm \ ( A ( 0 ; 2 ) \ ) và \ ( B ( 3 ; 0 ) \ ). Hãy viết phương trình tổng quát của đường thẳng đi qua hai điểm \ ( A ; B \ )

Cách giải:

Xem thêm: Top 5 phần mềm kiểm tra đạo văn tốt nhất 2022

Vì hai điểm \ ( A ; B \ ) nằm trên hai trục tọa độ nên ta sử dụng phương trình đường thẳng theo đoạn chắn :
\ ( AB : \ frac { x } { 3 } + \ frac { y } { 2 } = 1 \ )
\ ( \ Leftrightarrow 2 x + 3 y – 6 = 0 \ )

Viết phương trình đường thẳng đi qua 2 điểm có cùng hoành độ, tung độ

Phương trình đường thẳng đi qua hai điểm \ ( ( a ; y_1 ) \ ) và \ ( ( a ; y_2 ) \ ) có dạng : \ ( x = a \ )
Phương trình đường thẳng đi qua hai điểm \ ( ( x_1 ; b ) \ ) và \ ( ( x_2 ; b ) \ ) có dạng : \ ( y = b \ )

Ví dụ:

Trong mặt phẳng \ ( Oxy \ ) cho hai điểm \ ( A ( 7 ; 2 ) \ ) và \ ( B ( 100 ; 2 ) \ ). Hãy viết phương trình tổng quát của đường thẳng đi qua hai điểm \ ( A ; B \ )

Cách giải:

Vì hai điểm \ ( A, B \ ) có cùng tung độ nên
\ ( \ Rightarrow \ ) phương trình đường thẳng \ ( AB : y = 2 \ )

Cách viết phương trình đường thẳng đi qua 2 điểm cực trị

Bài toán: Cho hàm số bậc ba \( y=f(x) = ax^3+bx^2+cx+d \) có \( 2 \) điểm cực trị \( A(x_1;y_1) ; B(x_2;y_2) \). Hãy viết phương trình đường thẳng đi qua \( 2 \) điểm cực trị đó ?

Với những bài toán hàm số \ ( f ( x ) \ ) đã biết thì ta thuận tiện tìm ra tọa độ hai điểm cực trị rồi viết phương trình đường thẳng đi qua hai điểm đó
Với những bài toán mà hàm số \ ( f ( x ) \ ) có thông số chứa tham số \ ( m \ ) thì ta sẽ làm như sau để viết được phương trình đường thẳng chứa tham số \ ( m \ ) của hai điểm cực trị :

Cách giải:

Bước 1: Tính đạo hàm \ ( y ’ = 3 ax ^ 2 + 2 bx + c \ )
Bước 2: Chia hàm số \ ( y \ ) cho \ ( y ’ \ ) ta được :
- \ ( f ( x ) = Q ( x ). f ’ ( x ) + P ( x ) \ ) với \ ( P ( x ) = Ax + B \ ) là hàm số bậc nhất
Bước 3:Vì \ ( f ’ ( x_1 ) = f ’ ( x_2 ) = 0 \ ) nên :
- \ ( \ left \ { \ begin { matrix } y_1 = f ( x_1 ) = Ax_1 + B \ \ y_2 = f ( x_2 ) = Ax_2 + B \ end { matrix } \ right. \ Rightarrow \ ) phương trình đường thẳng là \ ( y = Ax + B \ )
- Từ những bước trên ta tính được công thức tính nhanh phương trình đường thẳng đi qua hai điểm cực trị của hàm số bậc ba \ ( y = f ( x ) = ax ^ 3 + bx ^ 2 + cx + d \ ) là :
- \ ( \ frac { 2 } { 3 } ( c – \ frac { b ^ 2 } { 3 a } ) x + ( d – \ frac { bc } { 9 a } ) \ )

Xem Thêm Cruise control là gì? chức năng và cách sử dụng như thế nào?

Ví dụ:

Cho hàm số \ ( y = 2 x ^ 3 + 3 ( m-1 ) x ^ 2 + 6 ( m – 2 ) x – 1 \ ). Tìm m để hàm số có đường thẳng đi qua hai điểm cực trị song song với đường thẳng \ ( y = – 4 x + 1 \ )

Cách giải:

Ta có : \ ( y ’ = 6 x ^ 2 + 6 ( m-1 ) x + 6 ( m-2 ) \ )
Hàm số có hai cực trị \ ( \ Leftrightarrow \ Delta = ( m-1 ) ^ 2-4 ( m-2 ) > 0 \ )
\ ( \ Leftrightarrow ( m-3 ) ^ 2 > 0 \ Leftrightarrow m \ neq 3 \ )
Để đường thẳng đi qua hai điểm cực trị song song với đường thẳng \ ( y = – 4 x + 1 \ ) thì thông số góc của đường thẳng đó phải bằng \ ( – 4 \ )
Áp dụng công thức tính nhanh ta có thông số góc của đường thẳng đi qua hai điểm cực trị là :
\ ( – 4 = \ frac { 2 } { 3 } [ 6 ( m-2 ) – \ frac { 9 ( m-1 ) ^ 2 } { 6 } ] = 4 ( m-2 ) – ( m-1 ) ^ 2 \ )
\ ( \ Leftrightarrow – ( m-3 ) ^ 2 = – 4 \ Leftrightarrow \ left [ \ begin { array } { l } m = 1 \ \ m = 5 \ end { array } \ right. \ )

Xem chi tiết >>> Cực trị hàm số bậc 3 và Công thức tính nhanh cực trị

Bài viết trên đây của DINHNGHIA.VN đã giúp bạn tổng hợp lý thuyết và một số ví dụ về bài toán viết phương trình đường thẳng đi qua hai điểm. Hy vọng những kiến thức trong bài viết sẽ giúp ích cho bạn trong quá trình học tập và nghiên cứu chủ đề viết phương trình đường thẳng đi qua 2 điểm. Chúc bạn luôn học tốt!

Tu khoa lien quan :