Viết phương trình đường tròn đi qua 3 điểm ( đường tròn ngoại tiếp tam giác )
A. Phương pháp viết phương trình đường tròn đi qua 3 điểm
Cho đường tròn ( C ) đi qua ba điểm A ; B và C. Lập phương trình đường tròn đi qua ba điểm :
1/ Bước 1: Gọi phương trình đường tròn là ( C): x2 + y2 – 2ax – 2by + c = 0 (*)
( với điều kiện kèm theo a2 + b2 – c > 0 ) .
2 / Bước 2 : Do điểm A ; B và C thuộc đường tròn nên thay tọa độ điểm A ; B và C vào ( * ) ta được phương trình ba phương trình ẩn a ; b ; c .
3 / Bước 3 : giải hệ phương trình ba ẩn a ; b ; c ta được phương trình đường tròn .

B. Ví dụ minh họa
Ví dụ 1: Đường tròn nào dưới đây đi qua 2 điểm A(1 ; 0) ; B( 3 ; 4) ?
A. x2 + y2 + 8x – 2y – 9 = 0 B. x2 + y2 – 3x – 16 = 0
C. x2 + y2 – x + y = 0 D. x2 + y2 – 4x – 4y + 3 = 0
Hướng dẫn giải
Thay tọa độ hai điểm A và B vào những giải pháp :
Điểm B ( 3 ; 4 ) không thuộc đường tròn A .
Điểm A ( 1 ; 0 ) không thuộc đường tròn B .
Điểm B ( 3 ; 4 ) không thuộc đường tròn C .
Điểm A ; B cùng thuộc đường tròn D .
Chọn D.
Ví dụ 2. Tìm tọa độ tâm đường tròn đi qua 3 điểm A( 0; 4); B( 2; 4) và C( 4; 0)
A. (0; 0) B. (1; 0) C. (3; 2) D. (1; 1)
Hướng dẫn giải
Phương trình đường tròn ( C ) có dạng :
x2 + y2 – 2 ax – 2 by + c = 0 ( a2 + b2 – c > 0 )
Do 3 điểm A; B; C thuộc (C) nên
Vậy tâm I ( 1 ; 1 )
Chọn D.
Ví dụ 3. Tìm bán kính đường tròn đi qua 3 điểm A(0; 4); B(3; 4); C(3; 0).
A. 5 B. 3 C. √6,25 D. √8
Hướng dẫn giải
Phương trình đường tròn ( C ) có dạng :
x2 + y2 – 2 ax – 2 by + c = 0 ( a2 + b2 – c > 0 )
Do 3 điểm A; B; C thuộc (C) nên
Vậy bán kính R = 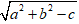
Chọn C.
Ví dụ 4. Cho tam giác ABC có A(-2; 4); B(5; 5) và C(6; -2). Đường tròn ngoại tiếp tam giác ABC có phương trình là:
A. x2 + y2 – 2x – y + 20 = 0 B. (x – 2)2 + (y – 1)2 = 20
C. x2 + y2 – 4x – 2y + 20 = 0 D. x2 + y2 – 4x – 2y – 20 = 0
Lời giải
Gọi đường tròn ngoại tiếp tam giác là ( C ) : x2 + y2 + 2 ax + 2 by + c = 0 ( a2 + b2 – c > 0 )
Do ba điểm A ; B và C thuộc đường tròn là :
Vậy đường tròn ( C ) cần tìm : x2 + y2 – 4 x – 2 y – 20 = 0
Chọn D.
Ví dụ 5. Cho tam giác ABC có A(1; -2); B(-3; 0); C(2; -2). Biết tam giác ABC nội tiếp đường tròn ( C). Tính bán kính đường tròn đó?
A. 5 B. 6 C. 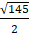
Lời giải
Gọi tam giác nội tiếp đường tròn ( C ) có phương trình là
x2 + y2 + 2 ax + 2 by + c = 0 ( a2 + b2 – c > 0 )
Do ba điểm A ; B và C thuộc đường tròn là :
⇒ Bán kính đường tròn ( C) là R =
Chọn C.
Ví dụ 6: Tâm của đường tròn qua ba điểm A( 2; 1); B( 2; 5) ; C( -2; 1) thuộc đường thẳng có phương trình
A. x – y + 3 = 0 B. x – y – 3 = 0 C. x + 2y – 3 = 0 D. x + y + 3 = 0
Hướng dẫn giải
Gọi phương trình ( C ) có dạng : x2 + y2 – 2 ax – 2 by + c = 0 ( a2 + b2 + c > 0 ). Tâm I ( a ; b )
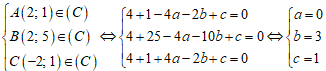
Lần lượt thế tọa độ I vào những phương trình để kiểm tra thì điểm I thuộc đường thẳng
x – y – 3 = 0
Chọn B.
Ví du 7: Cho tam giác ABC có A(2; 1); B( 3; 4) và C(-1; 2). Gọi I là tâm của đường tròn ngoại tiếp tam giác ABC. Tính OI?
A. 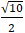
Lời giải
Ta có : AB → ( 1 ; 3 ) và AC → ( – 3 ; 1 )
⇒ AB →. AC → = 1. ( – 3 ) + 3.1 = 0
⇒ AB vuông góc AC nên tam giác ABC vuông tại A .
⇒ Tâm đường tròn ngoại tiếp tam giác ABC là trung điểm của cạnh huyền BC .
+ Tọa độ tâm I – trung điểm của BC là :
⇒ Khoảng cách OI = 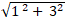
Chọn C.
Ví dụ 8: Tâm của đường tròn qua ba điểm A( 2; 1) ; B( 2; 5) và C( -2; 1) thuộc đường thẳng có phương trình
A. x – y + 3 = 0. B. x + y – 3 = 0 C. x – y – 3 = 0 D. x + y + 3 = 0
Hướng dẫn giải
Phương trình đường tròn ( C ) có dạng :
x2 + y2 – 2 ax – 2 by + c = 0 ( a2 + b2 – c > 0 )
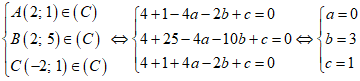
Vậy tâm đường tròn là I( 0; 3) .
Lần lượt thay tọa độ I vào những phương trình đường thẳng thì chỉ có đường thẳng
x – y + 3 = 0 thỏa mãn nhu cầu .
Chọn A.
Source: http://wp.ftn61.com
Category: Hỏi Đáp
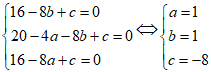
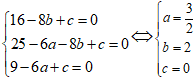
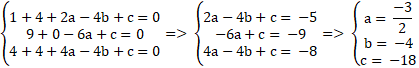
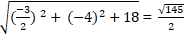
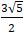
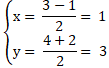


Để lại một bình luận