DAO ĐỘNG ĐIỀU HÒA
I. Lí thuyết về dao động điều hòa
1. DAO ĐỘNG CƠ
– Dao động cơ: Là chuyển động qua lại quanh một vị trí đặc biệt gọi là vị trí cân bằng.
Bạn đang đọc: Lý thuyết dao động điều hòa – http://wp.ftn61.com
– Dao động tuần hoàn: Là dao động mà trạng thái của vật được lặp lại như cũ, theo hướng cũ sau những khoảng thời gian bằng nhau xác định.
Dao động điều hòa: Là dao động trong đó li độ của vật là một hàm cosin (hay sin) của thời gian.
2.PHƯƠNG TRÌNH DAO ĐỘNG ĐIỀU HÒA
\ [ x = Ac { \ text { os ( } } \ omega { \ text { t + } } \ varphi { \ text { ) } } \ ]
Trong đó :
+ x : li độ của xê dịch
+ A : biên độ xê dịch
+ ω : tần số góc của giao động ( đơn vị chức năng : rad / s )
+ ωt + φ : pha của xê dịch tại thời gian t ( đơn vị chức năng : rad )
+ φ : pha bắt đầu của xê dịch
3. CÁC ĐẠI LƯỢNG TRONG DAO ĐỘNG ĐIỀU HÒA
– Chu kì T: Là khoảng thời gian để vật thực hiện được một dao động toàn phần.
Đơn vị của chu kì : s ( giây )
– Tần số f: Là số dao động toàn phần thực hiện được trong một giây.
Đơn vị của tần số : Hz ( héc )
– Tần số góc ω: Là đại lượng liên hệ với chu kì T hay với tần số f bằng hệ thức: $\omega = \dfrac{{2\pi }}{T} = 2\pi f$
Đơn vị của tần số góc : rad / s
– Một chu kì dao động vật đi được quãng đường là S = 4A
– Chiều dài quỹ đạo hoạt động của vật là L = 2A
– Vận tốc:
USD v = x ‘ = – \ omega A \ sin ( \ omega t + \ varphi ) = \ omega Acos ( \ omega t + \ varphi + \ dfrac { \ pi } { 2 } ) USD
+ Tại VTCB : tốc độ có độ lớn cực lớn : $ { v_ { { \ text { max } } } } = \ omega A $ .
+ Tại biên : tốc độ tốc bằng 0
+ Vận tốc nhanh pha hơn li độ một góc $ \ dfrac { \ pi } { 2 } $ và tốc độ đổi chiều tại biên độ .
– Gia tốc :
USD a = v ‘ = – { \ omega ^ 2 } A \ cos ( \ omega t + \ varphi ) = – { \ omega ^ 2 } x = { \ omega ^ 2 } A \ cos ( \ omega t + \ varphi + \ pi ) USD
+ Véc tơ tần suất luôn luôn hướng về vị trí cân đối
+ Có độ lớn tỉ lệ với độ lớn của li độ : $ \ left | a \ right | \ sim \ left | x \ right | $
+ Tại biên: gia tốc có độ lớn cực đại ${a_{{\text{max}}}} = {\omega ^2}A$, tại VTCB gia tốc bằng 0
+ Gia tốc nhanh pha hơn tốc độ một góc $ \ dfrac { \ pi } { 2 } $ và ngược pha so với li độ .
* Mô phỏng đồ thị li độ, vận tốc, gia tốc của dao động điều hòa
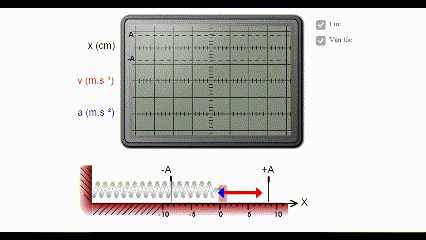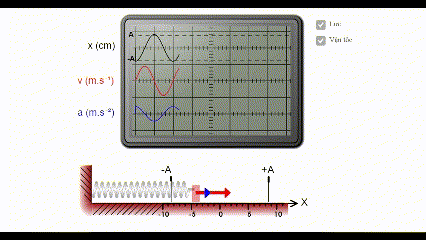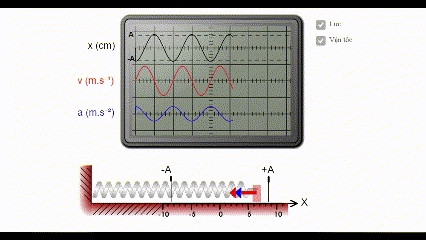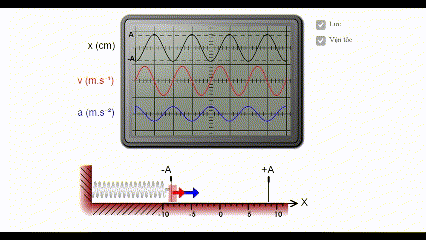
Ghi chú:
+ Công thức mối liên hệ giữa x, A, v hay A, a, v độc lập với thời hạn :\ ( \ begin { array } { l } x = A \ cos ( \ omega t + \ varphi ) \ to \ cos ( \ omega t + \ varphi ) = \ dfrac { x } { A } { \ rm { } } ( 1 ) \ \ v = x ‘ = – \ omega A \ sin ( \ omega t + \ varphi ) \ to \ sin ( \ omega t + \ varphi ) = – \ dfrac { v } { { A \ omega } } { \ rm { } } ( 2 ) \ \ a = v ‘ = – { \ omega ^ 2 } A \ cos ( \ omega t + \ varphi ) \ to \ cos ( \ omega t + \ varphi ) = – \ dfrac { a } { { { \ omega ^ 2 } A } } { \ rm { } } ( 3 ) \ end { array } \ )Từ ( 1 ) và ( 2 ) :USD \ to { \ cos ^ 2 } ( \ omega t + \ varphi ) + { \ sin ^ 2 } ( \ omega t + \ varphi ) = { ( \ dfrac { x } { A } ) ^ 2 } + { ( – \ dfrac { v } { { A \ omega } } ) ^ 2 } = 1 USD\ ( { A ^ 2 } = { x ^ 2 } + \ dfrac { { { v ^ 2 } } } { { { \ omega ^ 2 } } } \ )
Từ ( 2 ) và ( 3 ) :USD \ to { \ cos ^ 2 } ( \ omega t + \ varphi ) + { \ sin ^ 2 } ( \ omega t + \ varphi ) = { ( \ dfrac { a } { { A { \ omega ^ 2 } } } ) ^ 2 } + { ( – \ dfrac { v } { { A \ omega } } ) ^ 2 } = 1 USD
\ ( { A ^ 2 } = { \ dfrac { a } { { { \ omega ^ 4 } } } ^ 2 } + \ dfrac { { { v ^ 2 } } } { { { \ omega ^ 2 } } } \ )
![]() Những công thức suy ra từ những giá trị cực lớn :
Những công thức suy ra từ những giá trị cực lớn :
USD \ left \ { \ begin { gathered } { v_ { { \ text { max } } } } = A \ omega \ hfill \ \ { a_ { { \ text { max } } } } = A { \ omega ^ 2 } \ hfill \ \ \ end { gathered } \ right. \ to \ omega = \ dfrac { { { a_ { { \ text { max } } } } } } { { { v_ { { \ text { max } } } } } }, A = \ dfrac { { { v_ { { \ text { max } } } } ^ 2 } } { { { a_ { { \ text { max } } } } } } $
USD \ overline v = \ dfrac { s } { t } = \ dfrac { { 4A } } { T } = \ dfrac { { 4A \ omega } } { { 2 \ pi } } = \ dfrac { { 2 { v_ { { \ text { max } } } } } } { \ pi } $ ( trong đó $ \ overline v USD là vận tốc trung bình trong một chu kì )
4. MỐI LIÊN HỆ GIỮA DAO ĐỘNG ĐIỀU HÒA VÀ CHUYỂN ĐỘNG TRÒN ĐỀU
DĐĐH được xem là hình chiếu của một chất điểm hoạt động tròn đều lên một trục nằm trong mặt phẳng quỹ đạo. Với : USD A = R ; \ omega = \ dfrac { v } { R } $ .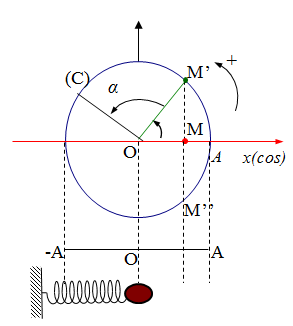
– Bước 1: Vẽ đường tròn (O, R = A);
– Bước 2: t = 0: xem vật đang ở đâu và bắt đầu chuyển động theo chiều âm hay dương
+ Nếu $ \ varphi > 0 USD : vật hoạt động theo chiều âm ( về biên âm )+ Nếu $ \ varphi < 0 USD : vật hoạt động theo chiều dương ( về biên dương )
– Bước 3: Xác định điểm tới để xác định góc quét $\alpha $: $\Delta t = \dfrac{{\alpha .T}}{{{{360}^0}}} \Rightarrow \alpha = \dfrac{{\Delta t{{.360}^0}}}{T}$
![]() Phương pháp tổng quát nhất để tính tốc độ, đường đi, thời hạn, hay vật qua vị trí nào đó trong quy trình giao động. Ta cho t = 0 để xem vật khởi đầu hoạt động từ đâu và đang đi theo chiều nào, sau đó dựa vào những vị trí đặc biệt quan trọng trên để tính .
Phương pháp tổng quát nhất để tính tốc độ, đường đi, thời hạn, hay vật qua vị trí nào đó trong quy trình giao động. Ta cho t = 0 để xem vật khởi đầu hoạt động từ đâu và đang đi theo chiều nào, sau đó dựa vào những vị trí đặc biệt quan trọng trên để tính .
5. ĐỒ THỊ CỦA DAO ĐỘNG ĐIỀU HÒA
Đồ thị của dao động điều hòa là một đường hình sin
– Đồ thị cho trường hơp φ = 0 .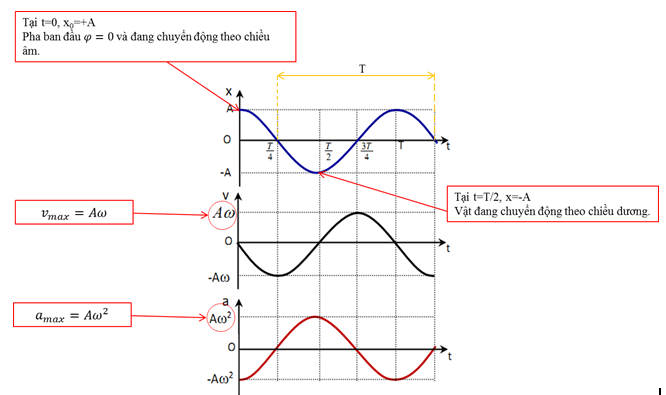
II. Sơ đồ tư duy lý thuyết về dao động điều hòa
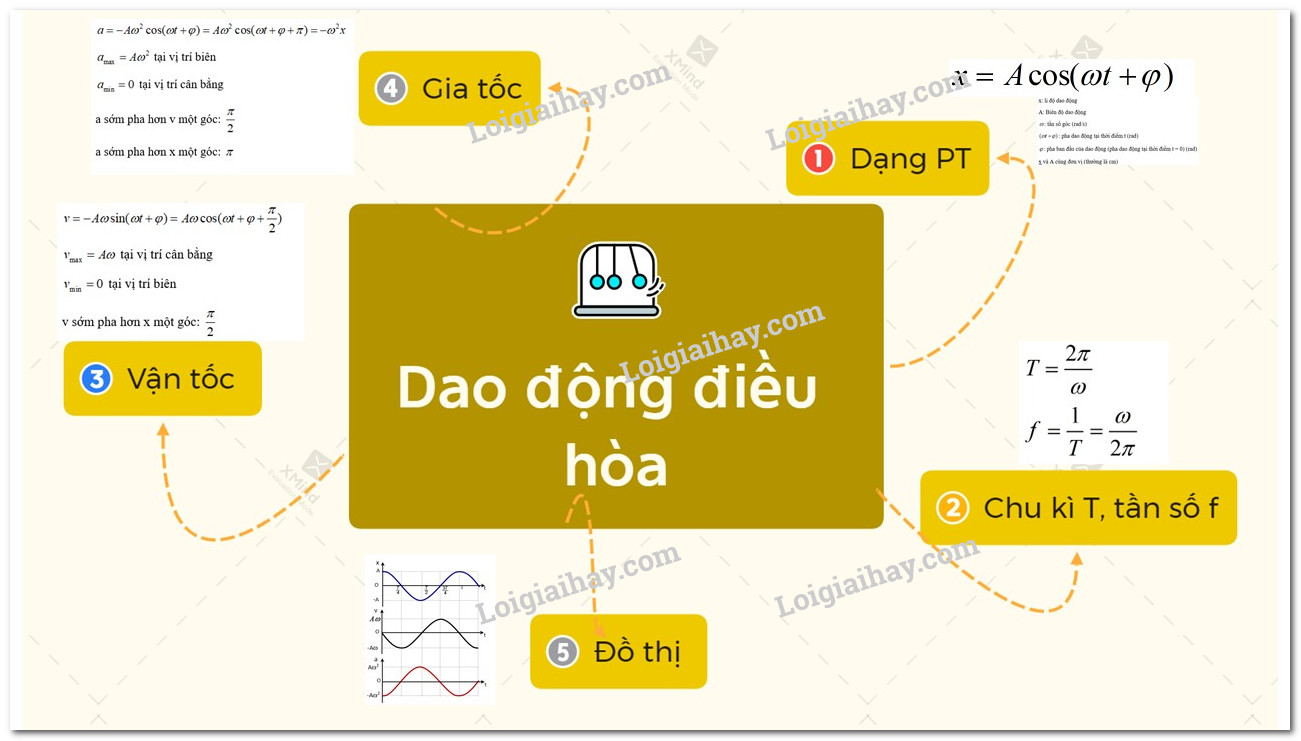
Source: http://wp.ftn61.com
Category: Hỏi Đáp


Để lại một bình luận