40 bài tập trắc nghiệm một số phương trình lượng giác thường gặp mức độ vận dụng, vận dụng cao

Câu hỏi 1 :Giải phương trình \ ( 2 { \ sin ^ 2 } 2 x + \ sin 7 x – 1 = \ sin x \ ) .

• A\(x = – \dfrac{\pi }{{18}} + \dfrac{{k\pi }}{3}\), \(x = \dfrac{{5\pi }}{{18}} + \dfrac{{k2\pi }}{9}\).

• B

  Bạn đang đọc: 40 bài tập trắc nghiệm một số phương trình lượng giác thường gặp mức độ vận dụng, vận dụng cao

  \(x = \pm \dfrac{\pi }{{18}} + {{k2\pi }}\), \(x = \dfrac{{5\pi }}{{18}} + \dfrac{{k2\pi }}{3}\).

• C\(x = \dfrac{\pi }{8} + \dfrac{{k\pi }}{4}\), \(x = \dfrac{\pi }{{18}} + \dfrac{{k2\pi }}{3}\), \(x = \dfrac{{5\pi }}{{18}} + \dfrac{{k2\pi }}{3}\).
• D\(x = \dfrac{\pi }{8} + \dfrac{{k\pi }}{4}\), \(x = \dfrac{\pi }{{18}} + \dfrac{{k\pi }}{18}\), \(x = – \dfrac{{5\pi }}{{18}} + \dfrac{{k\pi }}{3}\).

Đáp án: C

Phương pháp giải :- Nhóm \ ( 2 { \ sin ^ 2 } 2 x – 1 \ ), \ ( \ sin 7 x – \ sin x \ ) .
– Sử dụng công thức nhân đôi : \ ( \ cos 2 \ alpha = 1 – 2 { \ sin ^ 2 } \ alpha \ ), công thức đổi khác tổng thành tích : \ ( \ sin a – \ sin b = 2 \ cos \ dfrac { { a + b } } { 2 } \ sin \ dfrac { { a – b } } { 2 } \ ) .
– Đưa phương trình đã cho về dạng tích .
– Giải phương trình lượng giác cơ bản : \ ( \ sin x = \ sin \ alpha \ Leftrightarrow \ left [ \ begin { array } { l } x = \ alpha + k2 \ pi \ \ x = \ pi – \ alpha + k2 \ pi \ end { array } \ right. \, \, \ left ( { k \ in \ mathbb { Z } } \ right ) \ ) .Lời giải chi tiết cụ thể :\ ( \ begin { array } { l } \, \, \, \, \, \, 2 { \ sin ^ 2 } 2 x + \ sin 7 x – 1 = \ sin x \ \ \ Leftrightarrow \ left ( { 2 { { \ sin } ^ 2 } 2 x – 1 } \ right ) + \ sin 7 x – \ sin x = 0 \ \ \ Leftrightarrow – \ cos 4 x + 2 \ cos 4 x \ sin 3 x = 0 \ \ \ Leftrightarrow \ cos 4 x \ left ( { 2 \ sin 3 x – 1 } \ right ) = 0 \ \ \ Leftrightarrow \ left [ \ begin { array } { l } \ cos 4 x = 0 \ \ \ sin 3 x = \ dfrac { 1 } { 2 } \ end { array } \ right. \ \ \ Leftrightarrow \ left [ \ begin { array } { l } 4 x = \ dfrac { \ pi } { 2 } + k \ pi \ \ 3 x = \ dfrac { \ pi } { 6 } + k2 \ pi \ \ 3 x = \ dfrac { { 5 \ pi } } { 6 } + k2 \ pi \ end { array } \ right. \ Leftrightarrow \ left [ \ begin { array } { l } x = \ dfrac { \ pi } { 8 } + \ dfrac { { k \ pi } } { 4 } \ \ x = \ dfrac { \ pi } { { 18 } } + \ dfrac { { k2 \ pi } } { 3 } \ \ x = \ dfrac { { 5 \ pi } } { { 18 } } + \ dfrac { { k2 \ pi } } { 3 } \ end { array } \ right. \ end { array } \ )
Vậy nghiệm của phương trình là : \ ( x = \ dfrac { \ pi } { 8 } + \ dfrac { { k \ pi } } { 4 } \ ), \ ( x = \ dfrac { \ pi } { { 18 } } + \ dfrac { { k2 \ pi } } { 3 } \ ), \ ( x = \ dfrac { { 5 \ pi } } { { 18 } } + \ dfrac { { k2 \ pi } } { 3 } \ ) .

Chọn C.

Đáp án – Lời giải Câu hỏi 2 :Giải phương trình \ ( 1 + \ sin x + \ cos 3 x = \ cos x + \ sin 2 x + \ cos 2 x \ ) .

• A\(x = k\pi \), \(x = \dfrac{\pi }{6} + \dfrac{{k\pi }}{3}\), \(x = \dfrac{\pi }{{12}} + k\pi \), \(x = \dfrac{{5\pi }}{{7}} + k\pi \).
• B\(x = k2\pi \), \(x = \dfrac{\pi }{3} + \dfrac{{k2\pi }}{3}\), \(x = \dfrac{\pi }{{12}} + k\pi \), \(x = \dfrac{{5\pi }}{{12}} + k\pi \).
• C\(x = k\pi \), \(x = \dfrac{\pi }{3} + \dfrac{{k2\pi }}{3}\), \(x = \dfrac{\pi }{{12}} + k\pi \), \(x = \dfrac{{5\pi }}{{12}} + k\pi \).
• D\(x = k2\pi \), \(x = \dfrac{\pi }{6} + \dfrac{{k2\pi }}{3}\), \(x = \dfrac{\pi }{{12}} + k\pi \), \(x = \dfrac{{7\pi }}{{12}} + k\pi \).

Đáp án: C

Phương pháp giải :- Nhóm \ ( 1 – \ cos 2 x \ ), \ ( \ sin x – \ sin 2 x \ ), \ ( \ cos 3 x – \ cos x \ ) .
– Sử dụng công thức nhân đôi : \ ( 1 – \ cos 2 x = 2 { \ sin ^ 2 } x \ ), công thức đổi khác tổng thành tích : \ ( \ cos a – \ cos b = – 2 \ sin \ dfrac { { a + b } } { 2 } \ sin \ dfrac { { a – b } } { 2 } \ ) .
– Đưa phương trình đã cho về dạng tích .
– Giải phương trình lượng giác cơ bản : \ ( \ sin x = \ sin \ alpha \ Leftrightarrow \ left [ \ begin { array } { l } x = \ alpha + k2 \ pi \ \ x = \ pi – \ alpha + k2 \ pi \ end { array } \ right. \, \, \ left ( { k \ in \ mathbb { Z } } \ right ) \ ) .Lời giải chi tiết cụ thể :\ ( \ begin { array } { l } \, \, \, \, \, 1 + \ sin x + \ cos 3 x = \ cos x + \ sin 2 x + \ cos 2 x \ \ \ Leftrightarrow \ left ( { 1 – \ cos 2 x } \ right ) + \ left ( { \ sin x – \ sin 2 x } \ right ) + \ left ( { \ cos 3 x – \ cos x } \ right ) = 0 \ \ \ Leftrightarrow 2 { \ sin ^ 2 } 2 x + \ left ( { \ sin x – \ sin 2 x } \ right ) – 2 \ sin 2 x \ sin x = 0 \ \ \ Leftrightarrow 2 \ sin 2 x \ left ( { \ sin 2 x – \ sin x } \ right ) – \ left ( { \ sin 2 x – \ sin x } \ right ) = 0 \ \ \ Leftrightarrow \ left ( { \ sin 2 x – \ sin x } \ right ) \ left ( { 2 \ sin 2 x – 1 } \ right ) = 0 \ \ \ Leftrightarrow \ left [ \ begin { array } { l } \ sin 2 x = \ sin x \ \ \ sin 2 x = \ dfrac { 1 } { 2 } \ end { array } \ right. \ \ \ Leftrightarrow \ left [ \ begin { array } { l } 2 x = x + k2 \ pi \ \ 2 x = \ pi – x + k2 \ pi \ \ 2 x = \ dfrac { \ pi } { 6 } + k2 \ pi \ \ 2 x = \ dfrac { { 5 \ pi } } { 6 } + k2 \ pi \ end { array } \ right. \ Leftrightarrow \ left [ \ begin { array } { l } x = k2 \ pi \ \ x = \ dfrac { \ pi } { 3 } + \ dfrac { { k2 \ pi } } { 3 } \ \ x = \ dfrac { \ pi } { { 12 } } + k \ pi \ \ x = \ dfrac { { 5 \ pi } } { { 12 } } + k \ pi \ end { array } \ right. \ end { array } \ )
Vậy nghiệm của phương trình là : \ ( x = k2 \ pi \ ), \ ( x = \ dfrac { \ pi } { 3 } + \ dfrac { { k2 \ pi } } { 3 } \ ), \ ( x = \ dfrac { \ pi } { { 12 } } + k \ pi \ ), \ ( x = \ dfrac { { 5 \ pi } } { { 12 } } + k \ pi \ ) .

Đáp án – Lời giải Câu hỏi 3 :Giải phương trình \ ( \ cos 10 x – \ cos 8 x – \ cos 6 x + 1 = 0 \ ) .

• A\(x = \dfrac{{\pi }}{3} + k\pi\).
• B\(x = \dfrac{{\pi }}{3} + 2k\pi \), \(x = \dfrac{{k\pi }}{7}\).
• C\(x = \dfrac{{3k\pi }}{4}\)
• D\(x = \dfrac{{k\pi }}{4}\), \(x = \dfrac{{k\pi }}{3}\).

Đáp án: D

Phương pháp giải :- Sử dụng công thức biến hóa tổng thành tích : \ ( \ cos a – \ cos b = – 2 \ sin \ dfrac { { a + b } } { 2 } \ sin \ dfrac { { a – b } } { 2 } \ ) và công thức nhân đôi \ ( \ cos 2 \ alpha = 1 – 2 { \ sin ^ 2 } \ alpha \ ) .
– Đưa phương trình đã cho về dạng tích .
– Tiếp tục sử dụng công thức nhân đôi \ ( \ sin 2 \ alpha = 2 \ sin \ alpha \ cos \ alpha \ ) .
– Giải phương trình lượng giác cơ bản : \ ( \ cos x = \ cos \ alpha \ Leftrightarrow x = \ pm \ alpha + k2 \ pi \, \, \ left ( { k \ in \ mathbb { Z } } \ right ) \ ) .
– Kết hợp nghiệm .Lời giải chi tiết cụ thể :\ ( \ begin { array } { l } \, \, \, \, \, \, \ cos 10 x – \ cos 8 x – \ cos 6 x + 1 = 0 \ \ \ Leftrightarrow \ left ( { \ cos 10 x – \ cos 6 x } \ right ) + \ left ( { 1 – \ cos 8 x } \ right ) = 0 \ \ \ Leftrightarrow – 2 \ sin 8 x \ sin 2 x + 2 { \ sin ^ 2 } 4 x = 0 \ \ \ Leftrightarrow – 4 \ sin 4 x \ cos 4 x \ sin 2 x + 2 { \ sin ^ 2 } 4 x = 0 \ \ \ Leftrightarrow 2 \ sin 4 x \ left ( { – 2 \ cos 4 x \ sin 2 x + \ sin 4 x } \ right ) = 0 \ \ \ Leftrightarrow 2 \ sin 4 x \ left ( { – 2 \ cos 4 x \ sin 2 x + 2 \ sin 2 x \ cos 2 x } \ right ) = 0 \ \ \ Leftrightarrow 4 \ sin 4 x. \ sin 2 x \ left ( { – \ cos 4 x + \ cos 2 x } \ right ) = 0 \ \ \ Leftrightarrow 8 { \ sin ^ 2 } 2 x \ cos 2 x \ left ( { – \ cos 4 x + \ cos 2 x } \ right ) = 0 \ \ \ Leftrightarrow \ left [ \ begin { array } { l } \ sin 2 x = 0 \ \ \ cos 2 x = 0 \ \ \ cos 4 x = \ cos 2 x \ end { array } \ right. \ Leftrightarrow \ left [ \ begin { array } { l } 2 x = k \ pi \ \ 2 x = \ dfrac { \ pi } { 2 } + k \ pi \ \ 4 x = 2 x + k2 \ pi \ \ 4 x = – 2 x + k2 \ pi \ end { array } \ right. \ \ \ Leftrightarrow \ left [ \ begin { array } { l } x = \ dfrac { { k \ pi } } { 2 } \ \ x = \ dfrac { \ pi } { 4 } + \ dfrac { { k \ pi } } { 2 } \ \ x = k \ pi \ \ x = \ dfrac { { k \ pi } } { 3 } \ end { array } \ right. \ Leftrightarrow \ left [ \ begin { array } { l } x = \ dfrac { { k \ pi } } { 4 } \ \ x = \ dfrac { { k \ pi } } { 3 } \ end { array } \ right. \, \, \ left ( { k \ in \ mathbb { Z } } \ right ) \ end { array } \ )
Vậy nghiệm của phương trình là : \ ( x = \ dfrac { { k \ pi } } { 4 } \ ), \ ( x = \ dfrac { { k \ pi } } { 3 } \ ) .

Chọn D.

Đáp án – Lời giải Câu hỏi 4 :Giải phương trình \ ( \ sin 3 x – \ sin x + \ sin 2 x = 0 \ ) .

• A\(x = k\pi \), \(x = \dfrac{\pi }{3} + \dfrac{{k2\pi }}{3}\).
• B\(x =\pm \dfrac{\pi }{3} + \dfrac{{k2\pi }}{3}\).
• C\(x =  \dfrac{\pi }{2} + k\pi\), \(x = – \dfrac{\pi }{3} + \dfrac{{k2\pi }}{3}\).
• D\(x = 2k\pi \), \(x = \dfrac{\pi }{2} + \dfrac{{k\pi }}{3}\).

Đáp án: A

Phương pháp giải :- Sử dụng công thức biến hóa tổng thành tích : \ ( \ sin a – \ sin b = 2 \ cos \ dfrac { { a + b } } { 2 } \ sin \ dfrac { { a – b } } { 2 } \ ) và công thức nhân đôi \ ( \ sin 2 x = 2 \ sin x \ cos x \ ) .
– Đưa phương trình đã cho về dạng tích .
– Sử dụng biến hóa : \ ( \ ) .
– Giải phương trình lượng giác cơ bản : \ ( \ cos x = \ cos \ alpha \ Leftrightarrow x = \ pm \ alpha + k2 \ pi \, \, \ left ( { k \ in \ mathbb { Z } } \ right ) \ ) .Lời giải chi tiết cụ thể :\ ( \ begin { array } { l } \, \, \, \, \, \, \ sin 3 x – \ sin x + \ sin 2 x = 0 \ \ \ Leftrightarrow 2 \ cos 2 x \ sin x + 2 \ sin x \ cos x = 0 \ \ \ Leftrightarrow 2 \ sin x \ left ( { \ cos 2 x + \ cos x } \ right ) = 0 \ \ \ Leftrightarrow \ left [ \ begin { array } { l } \ sin x = 0 \ \ \ cos 2 x = – \ cos x = \ cos \ left ( { \ pi – x } \ right ) \ end { array } \ right. \ \ \ Leftrightarrow \ left [ \ begin { array } { l } x = k \ pi \ \ 2 x = \ pi – x + k2 \ pi \ \ 2 x = x – \ pi + k2 \ pi \ end { array } \ right. \ \ \ Leftrightarrow \ left [ \ begin { array } { l } x = k \ pi \ \ x = \ dfrac { \ pi } { 3 } + \ dfrac { { k2 \ pi } } { 3 } \ \ x = – \ pi + k2 \ pi \ end { array } \ right. \ Leftrightarrow \ left [ \ begin { array } { l } x = k \ pi \ \ x = \ dfrac { \ pi } { 3 } + \ dfrac { { k2 \ pi } } { 3 } \ end { array } \ right. \, \, \ left ( { k \ in \ mathbb { Z } } \ right ) \ end { array } \ )
Vậy nghiệm của phương trình là : \ ( x = k \ pi \ ), \ ( x = \ dfrac { \ pi } { 3 } + \ dfrac { { k2 \ pi } } { 3 } \ ) .

Chọn A.

Đáp án – Lời giải Câu hỏi 5 :Giải phương trình \ ( \ sin x + \ sin 2 x + \ sin 3 x + \ sin 4 x + \ sin 5 x + \ sin 6 x = 0 \ ) .

• A\(x = \dfrac{\pi }{6} + \dfrac{{k2\pi }}{3}\), \(x =  \pm \dfrac{{2\pi }}{3} + 2k\pi \).
• B\(x = \dfrac{{k2\pi }}{7}\), \(x = \dfrac{\pi }{3} + \dfrac{{k2\pi }}{3}\), \(x =  \pm \dfrac{{2\pi }}{3} + k2\pi \).
• C\(x = \dfrac{{k2\pi }}{3}\), \(x = \dfrac{\pi }{3} + \dfrac{{k2\pi }}{3}\), \(x =  + \dfrac{{\pi }}{7} + k2\pi \).
• D\(x = \dfrac{{k2\pi }}{7}+ k\pi \), \(x = \dfrac{2\pi }{3} + \dfrac{{k2\pi }}{3}\).

Đáp án: B

Phương pháp giải :- Sử dụng công thức biến hóa tổng thành tích : \ ( \ sin a + \ sin b = 2 \ sin \ dfrac { { a + b } } { 2 } \ cos \ dfrac { { a – b } } { 2 } \ ) .
– Đưa phương trình đã cho về dạng tích .
– Tiếp tục sử dụng công thức đổi khác tổng thành tích : \ ( \ cos a + \ cos b = 2 \ cos \ dfrac { { a + b } } { 2 } \ cos \ dfrac { { a – b } } { 2 } \ ) .
– Giải phương trình lượng giác cơ bản : \ ( \ cos x = \ cos \ alpha \ Leftrightarrow x = \ pm \ alpha + k2 \ pi \, \, \ left ( { k \ in \ mathbb { Z } } \ right ) \ ) .Lời giải chi tiết cụ thể :\ ( \ begin { array } { l } \, \, \, \, \, \, \ sin x + \ sin 2 x + \ sin 3 x + \ sin 4 x + \ sin 5 x + \ sin 6 x = 0 \ \ \ Leftrightarrow \ left ( { \ sin x + \ sin 6 x } \ right ) + \ left ( { \ sin 2 x + \ sin 5 x } \ right ) + \ left ( { \ sin 3 x + \ sin 4 x } \ right ) = 0 \ \ \ Leftrightarrow 2 \ sin \ dfrac { { 7 x } } { 2 } \ cos \ dfrac { { 5 x } } { 2 } + 2 \ sin \ dfrac { { 7 x } } { 2 } \ cos \ dfrac { { 3 x } } { 2 } + 2 \ sin \ dfrac { { 7 x } } { 2 } \ cos \ dfrac { x } { 2 } = 0 \ \ \ Leftrightarrow 2 \ sin \ dfrac { { 7 x } } { 2 } \ left ( { \ cos \ dfrac { { 5 x } } { 2 } + \ cos \ dfrac { { 3 x } } { 2 } + \ cos \ dfrac { x } { 2 } } \ right ) = 0 \ \ \ Leftrightarrow 2 \ sin \ dfrac { { 7 x } } { 2 } \ left [ { 2 \ cos \ dfrac { { 3 x } } { 2 } \ cos x + \ cos \ dfrac { { 3 x } } { 2 } } \ right ] = 0 \ \ \ Leftrightarrow 2 \ sin \ dfrac { { 7 x } } { 2 }. \ cos \ dfrac { { 3 x } } { 2 } \ left ( { 2 \ cos x + 1 } \ right ) = 0 \ \ \ Leftrightarrow \ left [ \ begin { array } { l } \ sin \ dfrac { { 7 x } } { 2 } = 0 \ \ \ cos \ dfrac { { 3 x } } { 2 } \ \ \ cos x = – \ dfrac { 1 } { 2 } \ end { array } \ right. \ Leftrightarrow \ left [ \ begin { array } { l } \ dfrac { { 7 x } } { 2 } = k \ pi \ \ \ dfrac { { 3 x } } { 2 } = \ dfrac { \ pi } { 2 } + k \ pi \ \ x = \ pm \ dfrac { { 2 \ pi } } { 3 } + k2 \ pi \ end { array } \ right. \ Leftrightarrow \ left [ \ begin { array } { l } x = \ dfrac { { k2 \ pi } } { 7 } \ \ x = \ dfrac { \ pi } { 3 } + \ dfrac { { k2 \ pi } } { 3 } \ \ x = \ pm \ dfrac { { 2 \ pi } } { 3 } + k2 \ pi \ end { array } \ right. \ end { array } \ )
Vậy nghiệm của phương trình là : \ ( x = \ dfrac { { k2 \ pi } } { 7 } \ ), \ ( x = \ dfrac { \ pi } { 3 } + \ dfrac { { k2 \ pi } } { 3 } \ ), \ ( x = \ pm \ dfrac { { 2 \ pi } } { 3 } + k2 \ pi \ ) .

Chọn A.

Đáp án – Lời giải Câu hỏi 6 :Giải phương trình \ ( \ cos x + \ cos 2 x + \ cos 3 x + \ cos 4 x = 0 \ ) .

• A\(x = \dfrac{\pi }{3} + k\pi \), \(x = k\pi \), \(x = \dfrac{{k\pi }}{5}\).
• B\(x = \dfrac{\pi }{2} + k\pi \), \(x = k2\pi \), \(x = \dfrac{{k2\pi }}{5}\).
• C\(x = \dfrac{\pi }{2} + 2k\pi \),  \(x = \dfrac{{k2\pi }}{3}\).
• D\(x = \pm \dfrac{\pi }{2} + k\pi \), \(x = k2\pi \)

Đáp án: B

Phương pháp giải :- Sử dụng công thức biến hóa tổng thành tích : \ ( \ cos a + \ cos b = 2 \ cos \ dfrac { { a + b } } { 2 } \ cos \ dfrac { { a – b } } { 2 } \ ) .
– Đưa phương trình đã cho về dạng tích .
– Giải phương trình lượng giác cơ bản : \ ( \ cos x = \ cos \ alpha \ Leftrightarrow x = \ pm \ alpha + k2 \ pi \, \, \ left ( { k \ in \ mathbb { Z } } \ right ) \ ) .Lời giải chi tiết cụ thể :\ ( \ begin { array } { l } \, \, \, \, \, \ cos x + \ cos 2 x + \ cos 3 x + \ cos 4 x = 0 \ \ \ Leftrightarrow \ left ( { \ cos x + \ cos 3 x } \ right ) + \ left ( { \ cos 2 x + \ cos 4 x } \ right ) = 0 \ \ \ Leftrightarrow 2 \ cos 2 x \ cos x + 2 \ cos 3 x \ cos x = 0 \ \ \ Leftrightarrow 2 \ cos x \ left ( { \ cos 2 x – \ cos 3 x } \ right ) = 0 \ \ \ Leftrightarrow \ left [ \ begin { array } { l } \ cos x = 0 \ \ \ cos 2 x = \ cos 3 x \ end { array } \ right. \ \ \ Leftrightarrow \ left [ \ begin { array } { l } x = \ dfrac { \ pi } { 2 } + k \ pi \ \ 3 x = 2 x + k2 \ pi \ \ 3 x = – 2 x + k2 \ pi \ end { array } \ right. \ \ \ Leftrightarrow \ left [ \ begin { array } { l } x = \ dfrac { \ pi } { 2 } + k \ pi \ \ x = k2 \ pi \ \ x = \ dfrac { { k2 \ pi } } { 5 } \ end { array } \ right. \, \, \ left ( { k \ in \ mathbb { Z } } \ right ) \ end { array } \ )
Vậy nghiệm của phương trình là : \ ( x = \ dfrac { \ pi } { 2 } + k \ pi \ ), \ ( x = k2 \ pi \ ), \ ( x = \ dfrac { { k2 \ pi } } { 5 } \ ) .

Chọn B.

Đáp án – Lời giải Câu hỏi 7 :

Giải phương trình \(1 + \cos x + \cos 2x + \cos 3x = 0\).

• A\(x =\pm \dfrac{\pi }{2} + 2k\pi \), \(x = \dfrac{\pi }{3} + \dfrac{{k\pi }}{3}\).
• B\(x = \dfrac{\pi }{2} + 2k\pi \), \(x = \pm \dfrac{\pi }{3} + \dfrac{{k2\pi }}{3}\).
• C\(x = \dfrac{\pi }{2} + k\pi \), \(x = \dfrac{\pi }{3} + \dfrac{{k2\pi }}{3}\).
• D\(x = – \dfrac{\pi }{2} + k\pi \), \(x = \dfrac{\pi }{6} + \dfrac{{k\pi }}{3}\).

Đáp án: C

Phương pháp giải :- Sử dụng công thức đổi khác tổng thành tích : \ ( \ cos a + \ cos b = 2 \ cos \ dfrac { { a + b } } { 2 } \ cos \ dfrac { { a – b } } { 2 } \ ) và công thức nhân đôi : \ ( 1 + \ cos 2 x = 2 { \ cos ^ 2 } x \ ) .
– Đưa phương trình đã cho về dạng tích .
– Sử dụng biến hóa : \ ( \ cos x = \ cos \ left ( { \ pi – x } \ right ) \ ) .
– Giải phương trình lượng giác cơ bản : \ ( \ cos x = \ cos \ alpha \ Leftrightarrow x = \ pm \ alpha + k2 \ pi \, \, \ left ( { k \ in \ mathbb { Z } } \ right ) \ ) .Lời giải chi tiết cụ thể :\ ( \ begin { array } { l } \, \, \, \, \, 1 + \ cos x + \ cos 2 x + \ cos 3 x = 0 \ \ \ Leftrightarrow \ left ( { 1 + \ cos 2 x } \ right ) + \ left ( { \ cos x + \ cos 3 x } \ right ) = 0 \ \ \ Leftrightarrow 2 { \ cos ^ 2 } x + 2 \ cos 2 x \ cos x = 0 \ \ \ Leftrightarrow 2 \ cos x \ left ( { \ cos x + \ cos 2 x } \ right ) = 0 \ \ \ Leftrightarrow \ left [ \ begin { array } { l } \ cos x = 0 \ \ \ cos x + \ cos 2 x = 0 \ end { array } \ right. \ \ \ Leftrightarrow \ left [ \ begin { array } { l } x = \ dfrac { \ pi } { 2 } + k \ pi \ \ \ cos 2 x = – \ cos x = \ cos \ left ( { \ pi – x } \ right ) \ end { array } \ right. \ \ \ Leftrightarrow \ left [ \ begin { array } { l } x = \ dfrac { \ pi } { 2 } + k \ pi \ \ 2 x = \ pi – x + k2 \ pi \ \ 2 x = x – \ pi + k2 \ pi \ end { array } \ right. \ Leftrightarrow \ left [ \ begin { array } { l } x = \ dfrac { \ pi } { 2 } + k \ pi \ \ 3 x = \ pi + k2 \ pi \ \ x = – \ pi + k2 \ pi \ end { array } \ right. \ \ \ Leftrightarrow \ left [ \ begin { array } { l } x = \ dfrac { \ pi } { 2 } + k \ pi \ \ x = \ dfrac { \ pi } { 3 } + \ dfrac { { k2 \ pi } } { 3 } \ \ x = – \ pi + k2 \ pi \ end { array } \ right. \ Leftrightarrow \ left [ \ begin { array } { l } x = \ dfrac { \ pi } { 2 } + k \ pi \ \ x = \ dfrac { \ pi } { 3 } + \ dfrac { { k2 \ pi } } { 3 } \ end { array } \ right. \ end { array } \ )
Vậy nghiệm của phương trình là : \ ( x = \ dfrac { \ pi } { 2 } + k \ pi \ ), \ ( x = \ dfrac { \ pi } { 3 } + \ dfrac { { k2 \ pi } } { 3 } \ ) .

Chọn C.

Đáp án – Lời giải Câu hỏi 8 :Giải phương trình \ ( \ sin x + \ sin 2 x + \ sin 3 x = \ cos x + \ cos 2 x + \ cos 3 x \ ) .

• A\(x =  \pm \dfrac{{2\pi }}{3} + k2\pi \), \(x = \dfrac{\pi }{8} + \dfrac{{k\pi }}{2}\).
• B\(x =  \pm \dfrac{{\pi }}{3} + k\pi \), \(x = \dfrac{\pi }{8} + \dfrac{{k\pi }}{3}\).
• C\(x =  + \dfrac{{4\pi }}{3} + k2\pi \), \(x = \dfrac{\pi }{8} + k\pi \).
• D\(x =  – \dfrac{{\pi }}{3} + k2\pi \), \(x = \dfrac{\pi }{8} + \dfrac{{k\pi }}{3}\).

Đáp án: A

Phương pháp giải :- Sử dụng công thức biến hóa tổng thành tích : \ ( \ sin a + \ sin b = 2 \ sin \ dfrac { { a + b } } { 2 } \ cos \ dfrac { { a – b } } { 2 } \ ) ,
\ ( \ cos a + \ cos b = 2 \ cos \ dfrac { { a + b } } { 2 } \ cos \ dfrac { { a – b } } { 2 } \ ) .
– Đưa phương trình đã cho về dạng tích .
– Giải phương trình lượng giác cơ bản : \ ( \ cos x = \ cos \ alpha \ Leftrightarrow x = \ pm \ alpha + k2 \ pi \, \, \ left ( { k \ in \ mathbb { Z } } \ right ) \ ), \ ( \ tan x = \ tan \ alpha \ Leftrightarrow x = \ alpha + k \ pi \, \, \ left ( { k \ in \ mathbb { Z } } \ right ) \ ) .Lời giải chi tiết cụ thể :\ ( \ begin { array } { l } \, \, \, \, \, \, \ sin x + \ sin 2 x + \ sin 3 x = \ cos x + \ cos 2 x + \ cos 3 x \ \ \ Leftrightarrow \ left ( { \ sin x + \ sin 3 x } \ right ) + \ sin 2 x = \ left ( { \ cos x + \ cos 3 x } \ right ) + \ cos 2 x \ \ \ Leftrightarrow 2 \ sin 2 x \ cos x + \ sin 2 x = 2 \ cos 2 x \ cos x + \ cos 2 x \ \ \ Leftrightarrow \ sin 2 x \ left ( { 2 \ cos x + 1 } \ right ) = \ cos 2 x \ left ( { 2 \ cos x + 1 } \ right ) \ \ \ Leftrightarrow \ left ( { 2 \ cos x + 1 } \ right ) \ left ( { \ sin 2 x – \ cos 2 x } \ right ) = 0 \ \ \ Leftrightarrow \ left [ \ begin { array } { l } 2 \ cos x + 1 = 0 \ \ \ sin 2 x – \ cos 2 x = 0 \ end { array } \ right. \ \ \ Leftrightarrow \ left [ \ begin { array } { l } \ cos x = – \ dfrac { 1 } { 2 } \ \ \ sin 2 x = \ cos 2 x \ end { array } \ right. \ \ \ Leftrightarrow \ left [ \ begin { array } { l } x = \ pm \ dfrac { { 2 \ pi } } { 3 } + k2 \ pi \ \ \ tan 2 x = 1 \ end { array } \ right. \ \ \ Leftrightarrow \ left [ \ begin { array } { l } x = \ pm \ dfrac { { 2 \ pi } } { 3 } + k2 \ pi \ \ 2 x = \ dfrac { \ pi } { 4 } + k \ pi \ end { array } \ right. \ \ \ Leftrightarrow \ left [ \ begin { array } { l } x = \ pm \ dfrac { { 2 \ pi } } { 3 } + k2 \ pi \ \ x = \ dfrac { \ pi } { 8 } + \ dfrac { { k \ pi } } { 2 } \ end { array } \ right. \, \, \ left ( { k \ in \ mathbb { Z } } \ right ) \ end { array } \ )
Vậy nghiệm của phương trình là : \ ( x = \ pm \ dfrac { { 2 \ pi } } { 3 } + k2 \ pi \ ), \ ( x = \ dfrac { \ pi } { 8 } + \ dfrac { { k \ pi } } { 2 } \ ) .

Chọn A.

Đáp án – Lời giải Câu hỏi 9 :Giải phương trình \ ( \ cos 11 x \ cos 3 x = \ cos 17 x \ cos 9 x \ ) .

• A\(x = \dfrac{{k\pi }}{3},\,\,x = \dfrac{{k\pi }}{{20}}\).
• B\(x = \dfrac{{k\pi }}{6},\,\,x = \dfrac{{k\pi }}{{20}}\).
• C\(x = \dfrac{{2k\pi }}{3},\,\,x = \dfrac{{k\pi }}{{20}}\).
• D\(x = \dfrac{{-k\pi }}{6},\,\,x = \dfrac{{k\pi }}{{20}}\).

Đáp án: B

Phương pháp giải :- Sử dụng công thức đổi khác tích thành tổng : \ ( \ cos a \ cos b = \ dfrac { 1 } { 2 } \ left [ { \ cos \ left ( { a + b } \ right ) + \ cos \ left ( { a – b } \ right ) } \ right ] \ ) .
– Giải phương trình lượng giác cơ bản : \ ( \ cos x = \ cos \ alpha \ Leftrightarrow x = \ pm \ alpha + k2 \ pi \, \, \ left ( { k \ in \ mathbb { Z } } \ right ) \ ) .Lời giải chi tiết cụ thể :\ ( \ begin { array } { l } \, \, \, \, \, \ cos 11 x \ cos 3 x = \ cos 17 x \ cos 9 x \ \ \ Leftrightarrow \ dfrac { 1 } { 2 } \ left ( { \ cos 14 x + \ cos 8 x } \ right ) = \ dfrac { 1 } { 2 } \ left ( { \ cos 26 x + \ cos 8 x } \ right ) \ \ \ Leftrightarrow \ cos 14 x + \ cos 8 x = \ cos 26 x + \ cos 8 x \ \ \ Leftrightarrow \ cos 14 x = \ cos 26 x \ \ \ Leftrightarrow \ left [ \ begin { array } { l } 26 x = 14 x + k2 \ pi \ \ 26 x = – 14 x + k2 \ pi \ end { array } \ right. \ \ \ Leftrightarrow \ left [ \ begin { array } { l } 12 x = k2 \ pi \ \ 40 x = k2 \ pi \ end { array } \ right. \ \ \ Leftrightarrow \ left [ \ begin { array } { l } x = \ dfrac { { k \ pi } } { 6 } \ \ x = \ dfrac { { k \ pi } } { { 20 } } \ end { array } \ right. \, \, \, \ left ( { k \ in \ mathbb { Z } } \ right ) \ end { array } \ )
Vậy nghiệm của phương trình là \ ( x = \ dfrac { { k \ pi } } { 6 }, \, \, x = \ dfrac { { k \ pi } } { { 20 } } \ ) .

Chọn B.

Đáp án – Lời giải Câu hỏi 10 :Cho phương trình \ ( 2 m { \ cos ^ 2 } x + 2 \ sin 2 x + m – 1 = 0 \ ). Có bao nhiêu số nguyên của m để phương trình trên có đúng một nghiệm thuộc \ ( \ left [ { 0 ; \ dfrac { \ pi } { 4 } } \ right ] \ ) ?

• A\(3\)
• B\(1\)
• C\(0\)
• D\(2\)

Đáp án: B

Phương pháp giải :- Xét hai trường hợp \ ( \ cos x = 0 \ ) và \ ( \ cos x \ ne 0 \ ) .
– Chia cả 2 vế của phương trình cho \ ( { \ cos ^ 2 } x \ ), đặt ẩn phụ \ ( t = \ tan x \ ) .
– Tìm khoảng chừng giá trị của \ ( t \ ) ứng với \ ( x \ in \ left [ { 0 ; \ dfrac { \ pi } { 4 } } \ right ] \ ) .
– Cô lập \ ( m \ ), đưa phương trình về dạng \ ( m = f \ left ( t \ right ) \ ) .
– Lập BBT của hàm số \ ( y = f \ left ( t \ right ) \ ) và Kết luận .Lời giải cụ thể :\ ( \ begin { array } { l } \, \, \, \, \, 2 m { \ cos ^ 2 } x + 2 \ sin 2 x + m – 1 = 0 \, \, \, \, \, \ left ( 1 \ right ) \ \ \ Leftrightarrow 2 m { \ cos ^ 2 } x + 4 \ sin x \ cos x + m – 1 = 0 \ end { array } \ )
TH1 : \ ( \ cos x = 0 \ Leftrightarrow m – 1 = 0 \ Leftrightarrow m = 1 \ ) .
Khi đó phương trình có nghiệm \ ( x = \ dfrac { \ pi } { 2 } + k \ pi \, \, \ left ( { k \ in \ mathbb { Z } } \ right ) \ ) .
Họ nghiệm này không có nghiệm thuộc \ ( \ left [ { 0 ; \ dfrac { \ pi } { 4 } } \ right ] \ Rightarrow m = 1 \ ) loại .
TH2 : \ ( \ cos x \ ne 0 \ ), chia cả 2 vế của phương trình cho \ ( { \ cos ^ 2 } x \ ) ta được :
\ ( \ begin { array } { l } \ Rightarrow 2 m + 4 \ tan x + \ left ( { m – 1 } \ right ) \ left ( { 1 + { { \ tan } ^ 2 } x } \ right ) = 0 \ \ \ Leftrightarrow \ left ( { m – 1 } \ right ) { \ tan ^ 2 } x + 4 \ tan x + 3 m – 1 = 0 \, \, \, \ left ( 2 \ right ) \ end { array } \ )
Đặt \ ( \ tan x = t \ ), với \ ( x \ in \ left [ { 0 ; \ dfrac { \ pi } { 4 } } \ right ] \ ) thì \ ( t \ in \ left [ { 0 ; 1 } \ right ] \ ), khi đó phương trình ( 2 ) trở thành :
\ ( \ left ( { m – 1 } \ right ) { t ^ 2 } + 4 t + 3 m – 1 = 0 \, \, \, \, \ left ( 3 \ right ) \ )
Để phương trình ( 1 ) có nghiệm duy nhất thuộc \ ( \ left [ { 0 ; \ dfrac { \ pi } { 4 } } \ right ] \ ) thì phương trình ( 3 ) có nghiệm \ ( t \ ) duy nhất thuộc \ ( \ left [ { 0 ; 1 } \ right ]. \ )
Ta có : \ ( \ left ( 3 \ right ) \ Leftrightarrow m \ left ( { { t ^ 2 } + 3 } \ right ) = { t ^ 2 } – 4 t + 1 \ ) \ ( \ Leftrightarrow m = \ dfrac { { { t ^ 2 } – 4 t + 1 } } { { { t ^ 2 } + 3 } } \, \, \ left ( * \ right ) \ )
Đặt \ ( g \ left ( t \ right ) = \ dfrac { { { t ^ 2 } – 4 t + 1 } } { { { t ^ 2 } + 3 } } \ ) ta có :
\ ( \ begin { array } { l } g ‘ \ left ( t \ right ) = \ dfrac { { \ left ( { 2 t – 4 } \ right ) \ left ( { { t ^ 2 } + 3 } \ right ) – \ left ( { { t ^ 2 } – 4 t + 1 } \ right ) 2 t } } { { { { \ left ( { { t ^ 2 } + 3 } \ right ) } ^ 2 } } } \ \ g ‘ \ left ( t \ right ) = \ dfrac { { 2 { t ^ 3 } + 6 t – 4 { t ^ 2 } – 12 – 2 { t ^ 3 } + 8 { t ^ 2 } – 2 t } } { { { { \ left ( { { t ^ 2 } + 3 } \ right ) } ^ 2 } } } \ \ g ‘ \ left ( t \ right ) = \ dfrac { { 4 { t ^ 2 } + 4 t – 12 } } { { { { \ left ( { { t ^ 2 } + 3 } \ right ) } ^ 2 } } } \ \ g ‘ \ left ( t \ right ) = 0 \ Leftrightarrow \ left [ \ begin { array } { l } t = \ dfrac { { – 1 + \ sqrt { 13 } } } { 2 } \, \, \, \ left ( { ktm } \ right ) \ \ t = \ dfrac { { – 1 – \ sqrt { 13 } } } { 2 } \, \, \, \ left ( { ktm } \ right ) \ end { array } \ right. \ end { array } \ )
Bảng biến thiên :

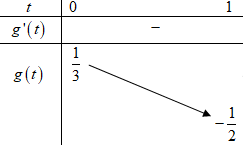
Để phương trình ( * ) có nghiệm duy nhất \ ( t \ in \ left [ { 0 ; 1 } \ right ] \ ) thì \ ( m \ in \ left [ { – \ dfrac { 1 } { 2 } ; \ dfrac { 1 } { 3 } } \ right ] \ ) .
Mà \ ( m \ in \ mathbb { Z } \ ) nên \ ( m = 0 \ ) .
Vậy có duy nhất một giá trị của \ ( m \ ) thỏa mãn nhu cầu nhu yếu bài toán .

Chọn B.

Đáp án – Lời giải Câu hỏi 11 :Số nghiệm của phương trình \ ( { \ left ( { { \ mathop { \ rm s } \ nolimits } { \ rm { in } } \ dfrac { x } { 2 } + \ cos \ dfrac { x } { 2 } } \ right ) ^ 2 } + \ sqrt 3 \ cos x = 2 \ ) với \ ( x \ in { \ rm { [ } } 0 ; \ pi { \ rm { ] } } \ ) là :

• A2.
• B1.
• C3.
• D0.

Đáp án: B

Phương pháp giải :Áp dụng chiêu thức giải phương trình \ ( a \ sin x + b \ cos x = c \ ) bằng cách chia cả 2 vế của phương trình cho \ ( \ sqrt { { a ^ 2 } + { b ^ 2 } } \ ), sau đó đưa phương trình về dạng phương trình lượng giác cơ bản .Lời giải chi tiết cụ thể :\ ( \ begin { array } { l } \, \, \, \, \, \, { \ left ( { \ sin \ dfrac { x } { 2 } + \ cos \ dfrac { x } { 2 } } \ right ) ^ 2 } + \ sqrt 3 \ cos x = 2 \ \ \ Leftrightarrow 1 + 2 \ sin \ dfrac { x } { 2 }. \ cos \ dfrac { x } { 2 } + \ sqrt 3 \ cos x = 2 \ \ \ Leftrightarrow \ sin x + \ sqrt 3 \ cos x = 1 \ \ \ Leftrightarrow \ dfrac { 1 } { 2 } \ sin x + \ dfrac { { \ sqrt 3 } } { 2 } \ cos x = \ dfrac { 1 } { 2 } \ \ \ Leftrightarrow \ sin \ left ( { \ dfrac { \ pi } { 6 } } \ right ). \ sin x + \ cos \ left ( { \ dfrac { \ pi } { 6 } } \ right ). \ cos x = \ dfrac { 1 } { 2 } \ \ \ Leftrightarrow \ cos \ left ( { x – \ dfrac { \ pi } { 6 } } \ right ) = \ cos \ dfrac { \ pi } { 3 } \ \ \ Leftrightarrow \ left [ \ begin { array } { l } x – \ dfrac { \ pi } { 6 } = \ dfrac { \ pi } { 3 } + k2 \ pi \ \ x – \ dfrac { \ pi } { 6 } = – \ dfrac { \ pi } { 3 } + l2 \ pi \ end { array } \ right. \ \ \ Leftrightarrow \ left [ \ begin { array } { l } x = \ dfrac { \ pi } { 2 } + k2 \ pi \ \ x = – \ dfrac { \ pi } { 6 } + l2 \ pi \ end { array } \ right. \, \, \, \ left ( { k, \, \, l \ in \ mathbb { Z } } \ right ) \ end { array } \ )
Mà \ ( x \ in \ left [ { 0 ; \ pi } \ right ] \ ), do đó \ ( \ left \ { \ begin { array } { l } 0 \ le \ dfrac { \ pi } { 2 } + k2 \ pi \ le \ pi \ \ 0 \ le – \ dfrac { \ pi } { 6 } + l2 \ pi \ le \ pi \ end { array } \ right. \ ) \ ( \ Leftrightarrow \ left \ { \ begin { array } { l } – \ dfrac { 1 } { 4 } \ le k \ le \ dfrac { 1 } { 4 } \ \ \ dfrac { 1 } { { 12 } } \ le l \ le \ dfrac { 7 } { { 12 } } \ end { array } \ right. \ Leftrightarrow \ left \ { \ begin { array } { l } k = 0 \ \ l \ in \ emptyset \ end { array } \ right .. \ )
Vậy phương trình đã cho có 1 nghiệm \ ( x = \ dfrac { \ pi } { 2 } \ ) thỏa mãn nhu cầu nhu yếu bài toán .

Chọn B.

Đáp án – Lời giải Câu hỏi 12 :Giải phương trình \ ( { \ sin ^ 2 } 3 x – { \ cos ^ 2 } 4 x = { \ sin ^ 2 } 5 x – { \ cos ^ 2 } 6 x. \ )

• A\(S = \left\{ {k\pi ;\frac{{k2\pi }}{9},\,\,k \in \mathbb{Z}} \right\}\)
• B\(S = \left\{ {\frac{{k\pi }}{2};\frac{{k2\pi }}{9},\,\,k \in \mathbb{Z}} \right\}\)
• C\(S = \left\{ {k\pi ;\frac{{k\pi }}{9},\,\,k \in \mathbb{Z}} \right\}\)
• D\(S = \left\{ {\frac{{k\pi }}{2};\frac{{k\pi }}{9},\,\,k \in \mathbb{Z}} \right\}\)

Đáp án: D

Lời giải chi tiết cụ thể :

\ ( \ begin { array } { l } \, \, \, \, \, \, \, { \ sin ^ 2 } 3 x – { \ cos ^ 2 } 4 x = { \ sin ^ 2 } 5 x – { \ cos ^ 2 } 6 x. \ \ \ Leftrightarrow \ frac { { 1 – \ cos 6 x } } { 2 } – \ frac { { 1 + \ cos 8 x } } { 2 } = \ frac { { 1 – \ cos 10 x } } { 2 } – \ frac { { 1 + \ cos 12 x } } { 2 } \ \ \ Leftrightarrow \ cos 6 x + \ cos 8 x = \ cos 10 x + \ cos 12 x \ \ \ Leftrightarrow 2 \ cos 7 x. \ cos x = 2 \ cos 11 x + \ cos 12 x \ \ \ Leftrightarrow 2 \ cos x \ left ( { \ cos 7 x – \ cos 11 x } \ right ) = 0 \ \ \ Leftrightarrow \ left [ \ begin { array } { l } \ cos x = 0 \ \ \ cos 7 x = \ cos 11 x \ end { array } \ right. \ Leftrightarrow \ left [ \ begin { array } { l } x = \ frac { \ pi } { 2 } + k2 \ pi \ \ 7 x = 11 x + k2 \ pi \ \ 7 x = – 11 x + k2 \ pi \ end { array } \ right. \, \ Leftrightarrow \ left [ \ begin { array } { l } x = \ frac { \ pi } { 2 } + k2 \ pi \ \ x = \ frac { { k \ pi } } { 2 } \ \ x = \ frac { { k \ pi } } { 9 } \ end { array } \ right. \, \, \ left ( { k \ in \ mathbb { Z } } \ right ) \ end { array } \ )
Vậy \ ( S = \ left \ { { \ frac { { k \ pi } } { 2 } ; \ frac { { k \ pi } } { 9 }, \, \, k \ in \ mathbb { Z } } \ right \ } \ ) .

Chọn D.

Đáp án – Lời giải Câu hỏi 13 :Tìm số điểm trình diễn những nghiệm của phương trình \ ( \ left | { \ sin x – \ cos x } \ right | + 8 \ sin x \ cos x = 1 \ ) trên đường tròn lượng giác .

• A\(2\)
• B\(3\)
• C\(1\)
• D\(4\)

Đáp án: D

Phương pháp giải :Đặt \ ( t = \ sin x – \ cos x \ ) tính \ ( \ sin x \ cos x = \ dfrac { { 1 – { t ^ 2 } } } { 2 } \ ) thay vào phương trình .
Giải phương trình và Kết luận .Lời giải cụ thể :Đặt \ ( t = \ sin x – \ cos x \ ) \ ( \ left ( { – \ sqrt 2 \ le t \ le \ sqrt 2 } \ right ) \ ) thì \ ( { t ^ 2 } = 1 – 2 \ sin x \ cos x \ ) \ ( \ Leftrightarrow \ sin x \ cos x = \ dfrac { { 1 – { t ^ 2 } } } { 2 } \ )
Thay vào phương trình ta được \ ( \ left | t \ right | + 8. \ dfrac { { 1 – { t ^ 2 } } } { 2 } = 1 \ ) \ ( \ Leftrightarrow 2 \ left | t \ right | + 8 – 8 { t ^ 2 } = 2 \ ) \ ( \ Leftrightarrow 8 { t ^ 2 } – 2 \ left | t \ right | – 6 = 0 \ )
\ ( \ Leftrightarrow \ left [ \ begin { array } { l } \ left | t \ right | = 1 \ \ \ left | t \ right | = – \ dfrac { 3 } { 4 } \ left ( { việt nam } \ right ) \ end { array } \ right. \ ) \ ( \ Leftrightarrow t = \ pm 1 \ left ( { TM } \ right ) \ )
TH1 : \ ( t = 1 \ ) thì \ ( \ sin x – \ cos x = 1 \ ) \ ( \ Leftrightarrow \ sqrt 2 \ sin \ left ( { x – \ dfrac { \ pi } { 4 } } \ right ) = 1 \ ) \ ( \ Leftrightarrow \ sin \ left ( { x – \ dfrac { \ pi } { 4 } } \ right ) = \ dfrac { 1 } { { \ sqrt 2 } } \ )
\ ( \ Leftrightarrow \ left [ \ begin { array } { l } x – \ dfrac { \ pi } { 4 } = \ dfrac { \ pi } { 4 } + k2 \ pi \ \ x – \ dfrac { \ pi } { 4 } = \ dfrac { { 3 \ pi } } { 4 } + k2 \ pi \ end { array } \ right. \ ) \ ( \ Leftrightarrow \ left [ \ begin { array } { l } x = \ dfrac { \ pi } { 2 } + k2 \ pi \ \ x = \ pi + k2 \ pi \ end { array } \ right. \ )
TH2 : \ ( \ sin x – \ cos x = – 1 \ ) \ ( \ Leftrightarrow \ sqrt 2 \ sin \ left ( { x – \ dfrac { \ pi } { 4 } } \ right ) = – 1 \ ) \ ( \ Leftrightarrow \ sin \ left ( { x – \ dfrac { \ pi } { 4 } } \ right ) = – \ dfrac { 1 } { { \ sqrt 2 } } \ )
\ ( \ Leftrightarrow \ left [ \ begin { array } { l } x – \ dfrac { \ pi } { 4 } = – \ dfrac { \ pi } { 4 } + k2 \ pi \ \ x – \ dfrac { \ pi } { 4 } = \ dfrac { { 5 \ pi } } { 4 } + k2 \ pi \ end { array } \ right. \ ) \ ( \ Leftrightarrow \ left [ \ begin { array } { l } x = k2 \ pi \ \ x = \ dfrac { { 3 \ pi } } { 2 } + k2 \ pi \ end { array } \ right. \ )
Vậy có bốn điểm trình diễn nghiệm của phương trình trên đường tròn lượng giác .

Chọn D.

Đáp án – Lời giải Câu hỏi 14 :Giải phương trình : \ ( { \ sin ^ 2 } x + 2 \ sqrt 3 \ sin x \ cos x – { \ cos ^ 2 } x = – 2 \ ) .

• A\(x =  \dfrac{\pi }{6} + k\pi \,\,\left( {k \in \mathbb{Z} } \right)\)
• B\(x =  – \dfrac{\pi }{6} + k\pi \,\,\left( {k \in \mathbb{Z} } \right)\)
• C\(x =  – \dfrac{\pi }{6} + k2\pi \,\,\left( {k \in \mathbb{Z} } \right)\)
• D\(x =  \dfrac{\pi }{6} + k2\pi \,\,\left( {k \in \mathbb{Z} } \right)\)

Đáp án: B

Phương pháp giải :– Xét thay vào phương trình và kiểm tra .
– Xét \ ( \ cos x \ ne 0 \ ) và chia cả hai vế của phương trình cho \ ( { \ cos ^ 2 } x \ ne 0 \ ) đưa về phương trình bậc hai ẩn \ ( \ tan x \ ) .
– Giải phương trình và Tóm lại nghiệm .Lời giải cụ thể :+ ) Xét \ ( \ cos x = 0 \ Leftrightarrow x = \ dfrac { \ pi } { 2 } + k \ pi \ ). Khi đó \ ( { \ sin ^ 2 } x = 1 – { \ cos ^ 2 } x = 1 \ ), thay vào phương trình ta được :
\ ( 1 + 0 – 0 = – 2 \ Leftrightarrow 1 = – 2 \ ) ( phi lí )
Suy ra \ ( x = \ dfrac { \ pi } { 2 } + k \ pi ; \, \, k \ in \ mathbb { Z } \ ) không phải là nghiệm .
+ ) Xét \ ( \ cos x \ ne 0 \ Leftrightarrow x \ ne \ dfrac { \ pi } { 2 } + k \ pi ; \, \, k \ in \ mathbb { Z } \ ), chia hai vế của phương trình cho \ ( { \ cos ^ 2 } x \ ne 0 \ ) ta được :
\ ( \ begin { array } { l } \ dfrac { { { { \ sin } ^ 2 } x } } { { { { \ cos } ^ 2 } x } } + \ dfrac { { 2 \ sqrt 3 \ sin x \ cos x } } { { { { \ cos } ^ 2 } x } } – \ dfrac { { { { \ cos } ^ 2 } x } } { { { { \ cos } ^ 2 } x } } = – \ dfrac { 2 } { { { { \ cos } ^ 2 } x } } \ \ \ Leftrightarrow { \ tan ^ 2 } x + 2 \ sqrt 3 \ tan x – 1 = – 2 \ left ( { 1 + { { \ tan } ^ 2 } x } \ right ) \ end { array } \ )
\ ( \ Leftrightarrow 3 { \ tan ^ 2 } x + 2 \ sqrt 3 \ tan x + 1 = 0 \ ) \ ( \ Leftrightarrow \ tan x = – \ dfrac { { \ sqrt 3 } } { 3 } \ ) \ ( \ Leftrightarrow x = \ dfrac { { – \ pi } } { 6 } + k \ pi, \, \, k \ in \ mathbb { Z } \ ) .Đáp án – Lời giải Câu hỏi 15 :Giải phương trình lượng giác sau : \ ( { \ sin ^ 2 } \ left ( { \ dfrac { x } { 2 } } \ right ) – 2 { \ cos ^ 2 } \ left ( { \ dfrac { x } { 4 } } \ right ) + \ dfrac { 3 } { 4 } = 0 \ ) .

• A\(x = \pi  + k2\pi \), \(k \in \mathbb{Z}\).
• B\(x = \pi  + k\pi \), \(k \in \mathbb{Z}\).
• C\(x = \dfrac{\pi }{2} + k\pi ,\,\,k \in \mathbb{R} \)
• D\(x = \dfrac{\pi }{2} + k2\pi ,\,\,k \in \mathbb{R} \)

Đáp án: A

Phương pháp giải :Sử dụng công thức hạ bậc \ ( { \ sin ^ 2 } \ alpha = \ dfrac { { 1 – \ cos 2 \ alpha } } { 2 } ; \ ) \ ( { \ cos ^ 2 } \ alpha = \ dfrac { { 1 + \ cos 2 \ alpha } } { 2 } \ )Lời giải chi tiết cụ thể :\ ( { \ sin ^ 2 } \ left ( { \ dfrac { x } { 2 } } \ right ) – 2 { \ cos ^ 2 } \ left ( { \ dfrac { x } { 4 } } \ right ) + \ dfrac { 3 } { 4 } = 0 \ )
\ ( \ Leftrightarrow \ dfrac { { 1 – \ cos x } } { 2 } – 2. \ dfrac { { 1 + \ cos \ dfrac { x } { 2 } } } { 2 } + \ dfrac { 3 } { 4 } = 0 \ ) \ ( \ Leftrightarrow 2 – 2 \ cos x – 4 – 4 \ cos \ dfrac { x } { 2 } + 3 = 0 \ )
\ ( \ Leftrightarrow \ left ( { 2 \ cos x – 1 } \ right ) + 4 \ cos \ dfrac { x } { 2 } = 0 \ ) \ ( \ Leftrightarrow { \ cos ^ 2 } \ dfrac { x } { 2 } + 4 \ cos \ dfrac { x } { 2 } = 0 \ ) \ ( \ Leftrightarrow \ cos \ dfrac { x } { 2 } \ left ( { \ cos \ dfrac { x } { 2 } + 4 } \ right ) = 0 \ )
\ ( \ Leftrightarrow \ left [ \ begin { array } { l } \ cos \ dfrac { x } { 2 } = 0 \ \ \ cos \ dfrac { x } { 2 } + 4 = 0 \ left ( { việt nam } \ right ) \ end { array } \ right. \ ) \ ( \ Leftrightarrow \ dfrac { x } { 2 } = \ dfrac { \ pi } { 2 } + k \ pi \ ) \ ( \ Leftrightarrow x = \ pi + k2 \ pi \ )
Vậy phương trình có nghiệm \ ( x = \ pi + k2 \ pi \ ), \ ( k \ in \ mathbb { Z } \ ) .Đáp án – Lời giải Câu hỏi 16 :Giải phương trình lượng giác sau : \ ( \ dfrac { { \ sin x + \ sin 2 x } } { { \ sin 3 x } } = – 1 \ ) .

• A\(x = \dfrac{\pi }{2} + k\pi \), \(k \in \mathbb{Z}\)
• B\(x = \dfrac{\pi }{2} + k2\pi \), \(k \in \mathbb{Z}\)
• C\(x =- \dfrac{\pi }{2} + k2\pi \), \(k \in \mathbb{Z}\)
• D\(x = \pm \dfrac{\pi }{4} + k\pi \), \(k \in \mathbb{Z}\)

Đáp án: A

Phương pháp giải :- Sử dụng công thức cộng \ ( \ sin a + \ sin b = 2 \ sin \ dfrac { { a + b } } { 2 } \ cos \ dfrac { { a – b } } { 2 } \ ) biến hóa phương trình về dạng tích .
– Giải phương trình và so sánh điều kiện kèm theo, Tóm lại nghiệm .Lời giải chi tiết cụ thể :ĐK : \ ( \ sin 3 x \ ne 0 \ Leftrightarrow 3 x \ ne k \ pi \ ) \ ( \ Leftrightarrow x \ ne \ dfrac { { k \ pi } } { 3 } \ )
PT \ ( \ Rightarrow \ sin x + \ sin 2 x = – \ sin 3 x \ ) \ ( \ Leftrightarrow \ left ( { \ sin x + \ sin 3 x } \ right ) + \ sin 2 x = 0 \ )
\ ( \ Leftrightarrow 2 \ sin 2 x \ cos x + \ sin 2 x = 0 \ ) \ ( \ Leftrightarrow \ sin 2 x \ left ( { 2 \ cos x + 1 } \ right ) = 0 \ )
\ ( \ Leftrightarrow \ left [ \ begin { array } { l } \ sin 2 x = 0 \ \ 2 \ cos x + 1 = 0 \ end { array } \ right. \ ) \ ( \ Leftrightarrow \ left [ \ begin { array } { l } \ sin 2 x = 0 \ \ \ cos x = – \ dfrac { 1 } { 2 } \ end { array } \ right. \ ) \ ( \ Leftrightarrow \ left [ \ begin { array } { l } 2 x = k \ pi \ \ x = \ pm \ dfrac { \ pi } { 3 } + k2 \ pi \ end { array } \ right. \ ) \ ( \ Leftrightarrow \ left [ \ begin { array } { l } x = \ dfrac { { k \ pi } } { 2 } \ \ x = \ pm \ dfrac { \ pi } { 3 } + k2 \ pi \ end { array } \ right., k \ in \ mathbb { Z } \ )
Biểu diễn những nghiệm trên đường tròn lượng giác ta được :

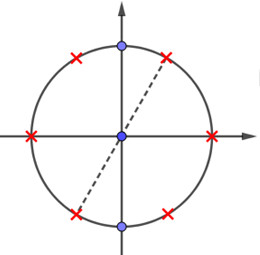
Quan sát hình vẽ ta thấy phương trình có nghiệm \ ( x = \ dfrac { \ pi } { 2 } + k \ pi \ ), \ ( k \ in \ mathbb { Z } \ ) ( hai điểm màu xanh ) .Đáp án – Lời giải Câu hỏi 17 :Giải phương trình \ ( \ sin 3 x + \ cos 2 x – \ sin x = 0 \ )

• A\(S = \left\{ {\frac{\pi }{6} + k2\pi ;\frac{{5\pi }}{6} + k2\pi ,\frac{\pi }{4} + \frac{{k\pi }}{2},k \in \mathbb{Z}} \right\}\)
• B\(S = \left\{ {\frac{{ – \pi }}{6} + k2\pi ;\frac{{7\pi }}{6} + k2\pi ,\frac{\pi }{4} + \frac{{k\pi }}{2},k \in \mathbb{Z}} \right\}\)
• C\(S = \left\{ {\frac{{ – \pi }}{6} + k2\pi ;\frac{{7\pi }}{6} + k2\pi ,\frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}\)
• D\(S = \left\{ {\frac{\pi }{6} + k2\pi ;\frac{{5\pi }}{6} + k2\pi ,\frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}\)

Đáp án: B

Lời giải chi tiết cụ thể :

\(\begin{array}{l}\,\,\,\,\,\,\,\sin 3x + \cos 2x – \sin x = 0\\ \Leftrightarrow 3\sin x – 4{\sin ^3}x + 1 – 2{\sin ^2}x – \sin x = 0\\ \Leftrightarrow  – 4{\sin ^3}x – 2{\sin ^2}x + 2\sin x + 1 = 0\\ \Leftrightarrow  – 2{\sin ^2}x\left( {2\sin x + 1} \right) + \left( {2\sin x + 1} \right) = 0\\ \Leftrightarrow \left( {2\sin x + 1} \right)\left( {1 – 2{{\sin }^2}x} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}2\sin x + 1 = 0\\1 – 2{\sin ^2}x = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\sin x = \frac{{ – 1}}{2}\\\cos 2x = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{{ – \pi }}{6} + k2\pi \\x = \frac{{7\pi }}{6} + k2\pi \\x = \frac{\pi }{4} + \frac{{k\pi }}{2}\end{array} \right.\,\,\,\,\,\,\,\left( {k \in \mathbb{Z}} \right)\end{array}\)

Vậy \ ( S = \ left \ { { \ frac { { – \ pi } } { 6 } + k2 \ pi ; \ frac { { 7 \ pi } } { 6 } + k2 \ pi, \ frac { \ pi } { 4 } + \ frac { { k \ pi } } { 2 }, k \ in \ mathbb { Z } } \ right \ } \ ) .

Chọn B.

Đáp án – Lời giải Câu hỏi 18 :Giải phương trình \ ( \ frac { { \ left ( { 1 + \ sin x + \ cos 2 x } \ right ) \ sin \ left ( { x + \ frac { \ pi } { 4 } } \ right ) } } { { 1 + \ tan x } } = \ frac { 1 } { { \ sqrt 2 } } \ cos x \, \, \, \ left ( 1 \ right ) \ )

• A\(S = \left\{ {\frac{{ – \pi }}{6} + k2\pi ;\frac{{7\pi }}{6} + k2\pi ;\,k \in \mathbb{Z} } \right\}\,\)
• B\(S = \left\{ {\frac{\pi }{6} + k2\pi ;\frac{{5\pi }}{6} + k2\pi ;\,k \in \mathbb{Z} } \right\}\,\)
• C\(S = \left\{ {\frac{{ – \pi }}{3} + k2\pi ;\frac{{4\pi }}{3} + k2\pi ;\,k \in \mathbb{Z} } \right\}\,\)
• D\(S = \left\{ {\frac{\pi }{3} + k2\pi ;\frac{{2\pi }}{3} + k2\pi ;\,k \in \mathbb{Z} } \right\}\,\)

Đáp án: A

Lời giải chi tiết cụ thể :\ ( \ frac { { \ left ( { 1 + \ sin x + \ cos 2 x } \ right ) \ sin \ left ( { x + \ frac { \ pi } { 4 } } \ right ) } } { { 1 + \ tan x } } = \ frac { 1 } { { \ sqrt 2 } } \ cos x \, \, \, \ left ( 1 \ right ) \ )
ĐK : \ ( \ left \ { \ begin { array } { l } \ tan x \ ne – 1 \ \ \ cos x \ ne 0 \ end { array } \ right. \ Leftrightarrow \ left \ { \ begin { array } { l } x \ ne \ frac { { – \ pi } } { 4 } + k \ pi \ \ x \ ne \ frac { \ pi } { 2 } + k \ pi \ end { array } \ right. \, \, \ left ( { k \ in \ mathbb { Z } } \ right ) \ )

\(\begin{array}{l}\left( 1 \right) \Leftrightarrow \left( {1 + \sin x + \cos 2x} \right).sin\left( {x + \frac{\pi }{4}} \right) = \frac{1}{{\sqrt 2 }}.\cos x.\frac{{\cos x + \sin x}}{{\cos x}}\\ \Leftrightarrow \left( {1 + \sin x + \cos 2x} \right).\sqrt 2 \sin \left( {x + \frac{\pi }{4}} \right) = \cos x + \sin x\\ \Leftrightarrow \left( {1 + \sin x + \cos 2x} \right).\left( {\sin x + \cos x} \right) = \cos x + \sin x\\ \Leftrightarrow \left( {\sin x + \cos x} \right).\left( {\sin x + \cos 2x} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}\sin x + \cos x = 0\\\sin x + \cos 2x = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\sin x + \cos x = 0\\\sin x + 1 – 2{\sin ^2}x = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\sqrt 2 .\sin \left( {x + \frac{\pi }{4}} \right) = 0\\\sin x = 1\\\sin x = \frac{{ – 1}}{2}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x =  – \frac{\pi }{4} + k\pi \,\,\left( {ktm} \right)\\x = \frac{\pi }{2} + k2\pi \,\,\,\left( {ktm} \right)\\x = \frac{{ – \pi }}{6} + k2\pi \,\,\left( {tm} \right)\\x = \frac{{7\pi }}{6} + k2\pi \,\,\left( {tm} \right)\end{array} \right.\end{array}\)

Vậy \ ( S = \ left \ { { \ frac { { – \ pi } } { 6 } + k2 \ pi ; \ frac { { 7 \ pi } } { 6 } + k2 \ pi ; \, k \ in \ mathbb { Z } } \ right \ } \, \ ) .

Chọn A.

Đáp án – Lời giải Câu hỏi 19 :Giải phương trình \ ( \ dfrac { 1 } { { \ cos x } } – \ dfrac { 1 } { { \ sin x } } = 2 \ sqrt 2 \ cos \ left ( { x + \ dfrac { \ pi } { 4 } } \ right ). \ )

• A\(S = \left\{ { \dfrac{{ \pi }}{4} + \dfrac{k\pi}{2}  ,\,\,k \in \mathbb{Z}} \right\}\).
• B\(S = \left\{ { – \dfrac{\pi }{4} + k2\pi ,\,\,k \in \mathbb{Z}} \right\}\)
• C\(S = \left\{ {\dfrac{\pi }{4} + k\pi ,\,\,k \in \mathbb{Z}} \right\}\)
• D\(S = \left\{ {\dfrac{\pi }{4} + k2\pi ,\,\,k \in \mathbb{Z}} \right\}\)

Đáp án: A

Lời giải cụ thể :\ ( \ dfrac { 1 } { { \ cos x } } – \ dfrac { 1 } { { \ sin x } } = 2 \ sqrt 2. \ cos \ left ( { x + \ dfrac { \ pi } { 4 } } \ right ) \, \, \, \, \ left ( 1 \ right ) \ )
ĐK : \ ( \ left \ { \ begin { array } { l } \ cos x \ ne 0 \ \ \ sin x \ ne 0 \ end { array } \ right. \ Leftrightarrow \ sin 2 x \ ne 0 \ Leftrightarrow x \ ne \ frac { { k \ pi } } { 2 } \, \, \ left ( { k \ in \ mathbb { Z } } \ right ) \ ) .
\ ( \ begin { array } { l } \ left ( 1 \ right ) \ Leftrightarrow \ dfrac { { \ sin x – \ cos x } } { { \ sin x. \ cos x } } = – 2 \ left ( { \ sin x – \ cos x } \ right ) \ \ \ Leftrightarrow \ left ( { \ sin x – \ cos x } \ right ) + 2. \ left ( { \ sin x – \ cos x } \ right ). \ sin x. \ cos x = 0 \ \ \ Leftrightarrow \ left ( { \ sin x – \ cos x } \ right ) \ left ( { 1 + \ sin 2 x } \ right ) = 0 \ \ \ Leftrightarrow \ left [ \ begin { array } { l } \ sin x – \ cos x = 0 \ \ 1 + \ sin 2 x = 0 \ end { array } \ right. \ Leftrightarrow \ left [ \ begin { array } { l } \ sqrt 2. \ sin \ left ( { x – \ dfrac { \ pi } { 4 } } \ right ) = 0 \ \ \ sin 2 x = – 1 \ end { array } \ right. \ \ \ Leftrightarrow \ left [ \ begin { array } { l } x – \ dfrac { \ pi } { 4 } = k \ pi \ \ 2 x = \ dfrac { { – \ pi } } { 2 } + k2 \ pi \ end { array } \ right. \ Leftrightarrow \ left [ \ begin { array } { l } x = \ frac { { \ pi } } { 4 } + k \ pi \ \ x = \ dfrac { { – \ pi } } { 4 } + k \ pi \ end { array } \ right. \ Leftrightarrow x = \ dfrac { { \ pi } } { 4 } + \ dfrac { k \ pi } { 2 } \, \, \, \ left ( { k \ in \ mathbb { Z } } \ right ) \ end { array } \ )
Vậy \ ( S = \ left \ { { \ dfrac { { \ pi } } { 4 } + \ dfrac { k \ pi } { 2 }, \, \, k \ in \ mathbb { Z } } \ right \ } \ ) .

Chọn A.

Đáp án – Lời giải Câu hỏi 20 :Giải phương trình \ ( \ sqrt 2 \ left ( { \ sin x – 2 \ cos x } \ right ) = 2 – \ sin 2 x \ )

• A\(S = \left\{ {\frac{{3\pi }}{4} + k2\pi ,\,\,k \in \mathbb{Z}} \right\}\)
• B\(S = \left\{ { \pm \frac{{3\pi }}{4} + k2\pi ,\,\,k \in \mathbb{Z}} \right\}\)
• C\(S = \left\{ { \pm \frac{{3\pi }}{4} + k\pi ,\,\,k \in \mathbb{Z}} \right\}\)
• D\(S = \left\{ {\frac{{3\pi }}{4} + k\pi ,\,\,k \in \mathbb{Z}} \right\}\)

Đáp án: B

Lời giải cụ thể :

\(\begin{array}{l}\,\,\,\,\,\,\,\sqrt 2 \left( {\sin x – 2\cos x} \right) = 2 – \sin 2x\\ \Leftrightarrow \sqrt 2 \left( {\sin x – 2\cos x} \right) = 2 – 2\sin x\cos x\\ \Leftrightarrow \sqrt 2 \sin x + 2\sin x.\cos x – 2\sqrt 2 \cos x – 2 = 0\\ \Leftrightarrow \sqrt 2 \sin x\left( {1 + \sqrt 2 \cos x} \right) – 2\left( {\sqrt 2 \cos x + 1} \right) = 0\\ \Leftrightarrow \left( {\sqrt 2 \sin x – 2} \right)\left( {1 + \sqrt 2 \cos x} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}\sqrt 2 \sin x – 2 = 0\\1 + \sqrt 2 \cos x = 0\end{array} \right. \Rightarrow \left[ \begin{array}{l}\sin x = \sqrt 2 \,\,\,\left( {loai} \right)\\\cos x = \frac{{ – 1}}{{\sqrt 2 }} = \cos \frac{{3\pi }}{4}\end{array} \right. \Leftrightarrow x =  \pm \frac{{3\pi }}{4} + 2k\pi \,\,\,\left( {k \in \mathbb{Z}} \right)\end{array}\)

Vậy \ ( S = \ left \ { { \ pm \ frac { { 3 \ pi } } { 4 } + k2 \ pi, \, \, k \ in \ mathbb { Z } } \ right \ } \ ) .

Chọn B.

Đáp án – Lời giải Câu hỏi 21 :Giải phương trình \ ( { \ rm { 2 sin } } x \ left ( { { \ rm { 1 } } + { \ rm { cos2 } } x } \ right ) + \ sin 2 x = { \ rm { 1 } } + { \ rm { 2 } } \ cos x \ )

• A\(S = \left\{ {\frac{{2\pi }}{3} + k2\pi ,\,\,\frac{\pi }{4} + k\pi ,\,\,k \in \mathbb{Z}} \right\}\)
• B\(S = \left\{ { \pm \frac{{2\pi }}{3} + k2\pi ,\,\,\frac{\pi }{4} + k\pi ,\,\,k \in \mathbb{Z}} \right\}\)
• C\(S = \left\{ { \pm \frac{{2\pi }}{3} + k2\pi ,\,\,\frac{\pi }{4} + k2\pi ,\,\,k \in \mathbb{Z}} \right\}\)
• D\(S = \left\{ {\frac{{2\pi }}{3} + k2\pi ,\,\,\frac{\pi }{4} + k2\pi ,\,\,k \in \mathbb{Z}} \right\}\)

Đáp án: B

Lời giải chi tiết cụ thể :\ ( \ begin { array } { l } \, \, \, \, \, \, \, { \ rm { 2 sin } } x \ left ( { { \ rm { 1 } } + { \ rm { cos2 } } x } \ right ) + \ sin 2 x = { \ rm { 1 } } + { \ rm { 2 } } \ cos x \ \ \ Leftrightarrow 2 \ sin x. 2 { \ cos ^ 2 } x + \ sin 2 x – 1 – 2 \ cos x = 0 \ \ \ Leftrightarrow 2 \ sin 2 x. \ cos x + \ sin 2 x – \ left ( { 1 + 2 \ cos x } \ right ) = 0 \ \ \ Leftrightarrow \ sin 2 x \ left ( { 2 \ cos x + 1 } \ right ) – \ left ( { 1 + 2 \ cos x } \ right ) = 0 \ \ \ Leftrightarrow \ left ( { \ sin 2 x – 1 } \ right ) \ left ( { 2 \ cos x + 1 } \ right ) = 0 \ \ \ Leftrightarrow \ left [ \ begin { array } { l } \ cos x = \ frac { { – 1 } } { 2 } \ \ \ sin 2 x = 1 \ end { array } \ right. \ Leftrightarrow \ left [ \ begin { array } { l } x = \ pm \ frac { { 2 \ pi } } { 3 } + k \ pi \ \ x = \ frac { \ pi } { 4 } + k \ pi \ end { array } \ right. \, \, \ left ( { k \ in \ mathbb { Z } } \ right ) \ end { array } \ )
Vậy \ ( S = \ left \ { { \ pm \ frac { { 2 \ pi } } { 3 } + k2 \ pi, \, \, \ frac { \ pi } { 4 } + k \ pi, \, \, k \ in \ mathbb { Z } } \ right \ } \ ) .

Chọn B.

Đáp án – Lời giải Câu hỏi 22 :Giải phương trình \ ( \ left ( { \ sin 2 x + \ cos { \ rm { 2 } } x } \ right ) \ cos x + 2 \ cos 2 x – \ sin x = 0 \ )

• A\(S = \left\{ {\frac{\pi }{4} + k\pi ,\,\,k \in \mathbb{Z}} \right\}\)
• B\(S = \left\{ {\frac{\pi }{2} + \frac{{k\pi }}{2},\,\,k \in \mathbb{Z}} \right\}\)
• C\(S = \left\{ {\frac{\pi }{4} + \frac{{k\pi }}{2},\,\,k \in \mathbb{Z}} \right\}\)
• D\(S = \left\{ {\frac{\pi }{2} + k\pi ,\,\,k \in \mathbb{Z}} \right\}\)

Đáp án: C

Lời giải cụ thể :\ ( \ begin { array } { l } \, \, \, \, \, \, \, \ left ( { \ sin 2 x + \ cos { \ rm { 2 } } x } \ right ) \ cos x + 2 \ cos 2 x – \ sin x = 0 \ \ \ Leftrightarrow \ sin 2 x. \ cos x + \ cos 2 x. \ cos x + 2. \ cos 2 x – \ sin x = 0 \ \ \ Leftrightarrow 2 \ sin x. { \ cos ^ 2 } x + \ left ( { \ cos x + 2 } \ right ). \ cos 2 x – \ sin x = 0 \ \ \ Leftrightarrow \ sin x \ left ( { 2 { { \ cos } ^ 2 } x – 1 } \ right ) + \ left ( { \ cos x + 2 } \ right ). \ cos 2 x = 0 \ \ \ Leftrightarrow \ sin x. \ cos 2 x + \ left ( { \ cos x + 2 } \ right ). \ cos 2 x = 0 \ \ \ Leftrightarrow \ cos 2 x. \ left ( { \ sin x + \ cos x + 2 } \ right ) = 0 \ Leftrightarrow \ left [ \ begin { array } { l } \ cos 2 x = 0 \ \ \ sin x + \ cos x + 2 = 0 \ end { array } \ right. \ \ \ Leftrightarrow \ left [ \ begin { array } { l } 2 x = \ frac { \ pi } { 2 } + k \ pi \ \ \ sqrt 2. \ sin \ left ( { x + \ frac { \ pi } { 4 } } \ right ) = – 2 \ end { array } \ right. \ Leftrightarrow \ left [ \ begin { array } { l } x = \ frac { \ pi } { 4 } + \ frac { { k \ pi } } { 2 } \, \, \, \ left ( { k \ in \ mathbb { Z } } \ right ) \ \ \ sin \ left ( { x + \ frac { \ pi } { 4 } } \ right ) = – \ sqrt 2 \, \, \ left ( { Loai } \ right ) \ end { array } \ right. \ end { array } \ )
Vậy \ ( S = \ left \ { { \ frac { \ pi } { 4 } + \ frac { { k \ pi } } { 2 }, \, \, k \ in \ mathbb { Z } } \ right \ } \ ) .

Chọn C.

Đáp án – Lời giải Câu hỏi 23 :Giải phương trình \ ( 3 \ sin x + 2 \ cos x = 2 + 3 \ tan x. \ )

• A\(S = \left\{ {k\pi ,\,\,\arctan \frac{2}{3} + k\pi ,\,\,k \in \mathbb{Z}} \right\}\)
• B\(S = \left\{ {k2\pi ,\,\,\arctan \frac{1}{3} + k\pi ,\,\,k \in \mathbb{Z}} \right\}\)
• C\(S = \left\{ {k\pi ,\,\,\arctan \frac{1}{3} + k\pi ,\,\,k \in \mathbb{Z}} \right\}\)
• D\(S = \left\{ {k2\pi ,\,\,\arctan \frac{2}{3} + k\pi ,\,\,k \in \mathbb{Z}} \right\}\)

Đáp án: D

Lời giải cụ thể :\ ( 3 \ sin x + 2 \ cos x = 2 + 3 \ tan x \, \, \, \ left ( 1 \ right ) \ ) .
Điều kiện : \ ( \ cos x \ ne 0 \ Leftrightarrow x \ ne \ frac { \ pi } { 2 } + k \ pi \, \, \ left ( { k \ in \ mathbb { Z } } \ right ) \ ) .
\ ( \ begin { array } { l } \ left ( 1 \ right ) \, \, \, \ Leftrightarrow 3 \ sin x \ cos x + 2 { \ cos ^ 2 } x = 2 \ cos x + 3 \ sin x \ \ \ Leftrightarrow 3 \ sin x \ cos x – 3 \ sin x + 2 { \ cos ^ 2 } x – 2 \ cos x = 0 \ \ \ Leftrightarrow 3 \ sin x \ left ( { \ cos x – 1 } \ right ) + 2 \ cos x \ left ( { \ cos x – 1 } \ right ) = 0 \ \ \ Leftrightarrow \ left ( { 3 \ sin x + 2 \ cos x } \ right ) \ left ( { \ cos x – 1 } \ right ) = 0 \ \ \ Leftrightarrow \ left [ \ begin { array } { l } 3 \ sin x + 2 \ cos x = 0 \ \ \ cos x – 1 = 0 \ end { array } \ right. \ Leftrightarrow \ left [ \ begin { array } { l } 3 \ tan x + 2 = 0 \ \ \ cos x = 1 \ end { array } \ right. \, \, \, \, \ \ \ Leftrightarrow \ left [ \ begin { array } { l } \ tan x = \ frac { { – 2 } } { 3 } \ \ \ cos x = 1 \ end { array } \ right. \ Leftrightarrow \ left [ \ begin { array } { l } x = \ arctan \ frac { { – 2 } } { 3 } + k \ pi \ left ( { tm } \ right ) \ \ x = k2 \ pi \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \ left ( { tm } \ right ) \ end { array } \ right. \ end { array } \ )
Vậy \ ( S = \ left \ { { k2 \ pi, \, \, \ arctan \ frac { 2 } { 3 } + k \ pi, \, \, k \ in \ mathbb { Z } } \ right \ } \ ) .

Chọn D.

Đáp án – Lời giải Câu hỏi 24 :Giải phương trình \ ( 2 \ sin 2 x – \ cos 2 x = 7 \ sin x + 2 \ cos x – 4 \ ) .

• A\(S = \left\{ {\frac{\pi }{6} + k\pi ;\frac{{5\pi }}{6} + k\pi ,k \in \mathbb{Z}} \right\}\)
• B\(S = \left\{ {\frac{\pi }{3} + k2\pi ;\frac{{2\pi }}{3} + k2\pi ,k \in \mathbb{Z}} \right\}\)
• C\(S = \left\{ {\frac{\pi }{3} + k\pi ;\frac{{2\pi }}{3} + k\pi ,k \in \mathbb{Z}} \right\}\)
• D\(S = \left\{ {\frac{\pi }{6} + k2\pi ;\frac{{5\pi }}{6} + k2\pi ,k \in \mathbb{Z}} \right\}\)

Đáp án: D

Lời giải cụ thể :

\(\begin{array}{l}\,\,\,\,\,\,2\sin 2x – \cos 2x = 7\sin x + 2\cos x – 4\\ \Leftrightarrow 4.\sin x.\cos x – 1 + 2{\sin ^2}x – 7\sin x – 2\cos x + 4 = 0\\ \Leftrightarrow \left( {4\sin x\cos x – 2\cos x} \right) + \left( {2{{\sin }^2}x – 7\sin x + 3} \right) = 0\\ \Leftrightarrow 2.\cos x.\left( {2\sin x – 1} \right) + \left( {2\sin x – 1} \right)\left( {\sin x – 3} \right) = 0\\ \Leftrightarrow \left( {2\sin x – 1} \right).\left( {2\cos x + \sin x – 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}\sin x = \frac{1}{2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\2\cos x + \sin x = 3\,\,\left( 2 \right)\end{array} \right.\end{array}\)

+ ) Xét \ ( \ left ( 1 \ right ) \ Leftrightarrow \ left [ \ begin { array } { l } x = \ frac { \ pi } { 6 } + k2 \ pi \ \ x = \ frac { { 5 \ pi } } { 6 } + k2 \ pi \, \, \, \, \, \ end { array } \ right. \, \ left ( { k \ in \ mathbb { Z } } \ right ) \ ) .
+ ) Xét \ ( \ left ( 2 \ right ) : \, \, \ sin x + 2 \ cos x = 3 \ ) .
Ta có : \ ( \ sqrt { { A ^ 2 } + { B ^ 2 } } = \ sqrt { { 1 ^ 2 } + { 2 ^ 2 } } = \ sqrt 5 < \ sqrt { { 3 ^ 2 } } = 3 \ Rightarrow \ ) Phương trình ( 2 ) vô nghiệm . Vậy \ ( S = \ left \ { { \ frac { \ pi } { 6 } + k2 \ pi ; \ frac { { 5 \ pi } } { 6 } + k2 \ pi, k \ in \ mathbb { Z } } \ right \ } \ ) .

Chọn D.

Đáp án – Lời giải Câu hỏi 25 :Giải phương trình \ ( 3 \ left ( { \ tan x + \ cot x } \ right ) = 2 \ left ( { 2 + \ sin 2 x } \ right ). \ )

• A\(S = \left\{ {\frac{\pi }{4} + k2\pi ;\,\,\pi  + k2\pi } \right\}\)
• B\(S = \left\{ { – \frac{\pi }{2} + k2\pi ;\,\, – \pi  + k2\pi } \right\}\)
• C\(S = \left\{ { \frac{\pi }{4} + k\pi } \right\}\)
• D\(S = \left\{ {\frac{\pi }{4} + k2\pi ;\,\, – \pi  + k2\pi } \right\}\)

Đáp án: C

Lời giải cụ thể :\ ( \ begin { array } { l } 3 \ left ( { \ tan x + \ cot x } \ right ) = 2 \ left ( { 2 + \ sin 2 x } \ right ) \, \, \, \, \ left ( { x \ ne \ dfrac { { k \ pi } } { 2 }, \, \, k \ in \ mathbb { Z } } \ right ) \ \ \ Leftrightarrow 3 \ left ( { \ dfrac { { \ sin x } } { { \ cos x } } + \ dfrac { { \ cos x } } { { \ sin x } } } \ right ) = 2 \ left ( { 2 + 2 \ sin x. \ cos x } \ right ) \ \ \ Leftrightarrow 3. \ dfrac { 1 } { { \ sin x. \ cos x } } = 4 \ left ( { 1 + \ sin x. \ cos x } \ right ) \ end { array } \ )
Đặt \ ( \ sin x.cosx = t \, \, \, \, \ left ( { t \ ne 0 } \ right ) \ ), khi đó phương trình trở thành :
\ ( \ begin { array } { l } 3. \ dfrac { 1 } { t } = 4 \ left ( { 1 + t } \ right ) \ Leftrightarrow – 4 { t ^ 2 } – 4 t + 3 = 0 \ Leftrightarrow \ left [ \ begin { array } { l } t = \ dfrac { 1 } { 2 } \ \ t = \ dfrac { { – 3 } } { 2 } \ end { array } \ right. \, \, \, \ left ( { tm } \ right ) \ \ \ Leftrightarrow \ left [ \ begin { array } { l } \ sin x. \ cos x = \ dfrac { 1 } { 2 } \ \ \ sin x. \ cos x = \ dfrac { { – 3 } } { 2 } \ end { array } \ right. \ Leftrightarrow \ left [ \ begin { array } { l } \ dfrac { 1 } { 2 } \ sin 2 x = \ dfrac { 1 } { 2 } \ \ \ dfrac { 1 } { 2 } \ sin 2 x = \ dfrac { { – 3 } } { 2 } \ end { array } \ right. \ \ \ Leftrightarrow \ left [ \ begin { array } { l } \ sin 2 x = 1 \ \ \ sin 2 x = – 3 \, \, \ left ( { loai } \ right ) \ end { array } \ right. \ Leftrightarrow 2 x = \ dfrac { \ pi } { 2 } + k2 \ pi \ Leftrightarrow x = \ dfrac { \ pi } { 4 } + k \ pi \, \, \ left ( { k \ in \ mathbb { Z } } \ right ) \, \, \ left ( { tm } \ right ) \ end { array } \ )
Vậy \ ( S = \ left \ { { \ dfrac { \ pi } { 4 } + k \ pi \, , \, \, k \ in \ mathbb { Z } } \ right \ } \ ) .Đáp án – Lời giải Câu hỏi 26 :Giải phương trình \ ( 2 { \ sin ^ 3 } x – \ cos 2 x + \ cos x = 0. \ )

• A\(x =  – \dfrac{\pi }{4} + k\pi ,\,\,x = k2\pi \)
• B\(x =  \dfrac{\pi }{4} + k\pi ,\,\,x = k2\pi \)
• C\(x =  – \dfrac{\pi }{4} + k\pi ,\,\,x = k\pi \)
• D\(x =  \dfrac{\pi }{4} + k\pi ,\,\,x = k\pi \)

Đáp án: A

Lời giải cụ thể :\ ( \ begin { array } { l } \, \, \, \, \, \, \, 2 { \ sin ^ 3 } x – \ cos 2 x + \ cos x = 0 \ \ \ Leftrightarrow 2 \ left ( { 1 – { { \ cos } ^ 2 } x } \ right ). \ sin x + \ left ( { – 2 { { \ cos } ^ 2 } x + \ cos x + 1 } \ right ) = 0 \ \ \ Leftrightarrow 2 \ left ( { 1 – \ cos x } \ right ) \ left ( { 1 + \ cos x } \ right ). \ sin x + \ left ( { 1 – \ cos x } \ right ) \ left ( { 2 \ cos x + 1 } \ right ) = 0 \ \ \ Leftrightarrow \ left ( { 1 – \ cos x } \ right ) \ left [ { 2 \ sin x \ left ( { 1 + \ cos x } \ right ) + 2 \ cos x + 1 } \ right ] = 0 \ \ \ Leftrightarrow \ left [ \ begin { array } { l } \ cos x = 1 \, \, \, \ left ( 1 \ right ) \ \ 2 \ sin x + 2 \ sin x \ cos x + 2 \ cos x + 1 = 0 \, \, \, \ left ( 2 \ right ) \ end { array } \ right. \ \ \ left ( 1 \ right ) \ Leftrightarrow x = k2 \ pi \, \, \, \ left ( { k \ in \ mathbb { Z } } \ right ) \ \ \ left ( 2 \ right ) \ Leftrightarrow 2 \ left ( { \ sin x + \ cos x } \ right ) + 2 \ sin x \ cos x + 1 = 0 \ end { array } \ )
Đặt \ ( \ sin x + \ cos x = t \, \, \, \, \ left ( { – \ sqrt 2 \ le t \ le \ sqrt 2 } \ right ) \ ), khi đó ta có :

\(\begin{array}{l}{\left( {\sin x + cosx} \right)^2} = {t^2} \Leftrightarrow {\sin ^2}x + 2\sin x.\cos x + {\cos ^2}x = {t^2}\\ \Leftrightarrow 1 + 2\sin x.\cos x = {t^2} \Leftrightarrow \sin x.\cos x = \dfrac{{{t^2} – 1}}{2}\end{array}\)
Phương trình (2) trở thành:

\ ( \ begin { array } { l } 2 t + 2. \ dfrac { { { t ^ 2 } – 1 } } { 2 } + 1 = 0 \ Leftrightarrow { t ^ 2 } + 2 t = 0 \ Leftrightarrow \ left [ \ begin { array } { l } t = 0 \, \, \, \, \, \, \, \ left ( { tm } \ right ) \ \ t = – 2 \, \, \ left ( { ktm } \ right ) \ end { array } \ right. \ \ \ Rightarrow \ sin x + \ cos x = 0 \ Leftrightarrow \ sqrt 2 \ sin \ left ( { x + \ dfrac { \ pi } { 4 } } \ right ) = 0 \ \ \ Leftrightarrow \ sin \ left ( { x + \ dfrac { \ pi } { 4 } } \ right ) = 0 \ Leftrightarrow x = \ dfrac { { – \ pi } } { 4 } + k \ pi \, \, \, \ left ( { k \ in \ mathbb { Z } } \ right ). \ end { array } \ )
Vậy \ ( S = \ left \ { { – \ dfrac { \ pi } { 4 } + k \ pi \, , \, \, k \ in \ mathbb { Z } } \ right \ } \ ) .Đáp án – Lời giải Câu hỏi 27 :Giải phương trình \ ( { \ sin ^ 3 } x + { \ cos ^ 3 } x = 2 \ left ( { \ sin x + \ cos x } \ right ) – 1. \ )

• A\(S = \left\{ {\frac{\pi }{2} + k\pi ;\,\,\pi  + k\pi } \right\}\)
• B\(S = \left\{ {\frac{\pi }{2} + k2\pi ;\,\,\pi  + k2\pi } \right\}\)
• C\(S = \left\{ {\frac{\pi }{2} + k2\pi ;\,\,k2\pi } \right\}\)
• D\(S = \left\{ {\frac{\pi }{2} + k\pi ;\,\,\,k\pi } \right\}\)

Đáp án: C

Lời giải cụ thể :\ ( \ begin { array } { l } \, \, \, \, \, \, \, { \ sin ^ 3 } x + { \ cos ^ 3 } x = 2 \ left ( { \ sin x + \ cos x } \ right ) – 1 \ \ \ Leftrightarrow \ left ( { \ sin x + \ cos x } \ right ) \ left ( { 1 – \ sin x. \ cos x } \ right ) – 2 \ left ( { \ sin x + \ cos x } \ right ) + 1 = 0 \ \ \ Leftrightarrow \ left ( { \ sin x + \ cos x } \ right ) \ left ( { – 1 – \ sin x. \ cos x } \ right ) + 1 = 0 \ end { array } \ )
Đặt \ ( \ sin x + \ cos x = t \, \, \, \, \ left ( { – \ sqrt 2 \ le t \ le \ sqrt 2 } \ right ) \ ), khi đó ta có :

\(\begin{array}{l}{\left( {\sin x + cosx} \right)^2} = {t^2} \Leftrightarrow {\sin ^2}x + 2\sin x.\cos x + {\cos ^2}x = {t^2}\\ \Leftrightarrow 1 + 2\sin x.\cos x = {t^2} \Leftrightarrow \sin x.\cos x = \dfrac{{{t^2} – 1}}{2}\end{array}\)
Phương trình trở thành:

\ ( \ begin { array } { l } \ Rightarrow t \ left ( { – 1 – \ dfrac { { { t ^ 2 } – 1 } } { 2 } } \ right ) + 1 = 0 \ Leftrightarrow t \ left ( { – { t ^ 2 } – 1 } \ right ) + 2 = 0 \ Leftrightarrow – { t ^ 3 } – t + 2 = 0 \ Leftrightarrow t = 1 \ \ \ Leftrightarrow \ sin x + cosx = 1 \ Leftrightarrow \ sqrt 2 \ sin \ left ( { x + \ dfrac { \ pi } { 4 } } \ right ) = 1 \ Leftrightarrow \ sin \ left ( { x + \ dfrac { \ pi } { 4 } } \ right ) = \ dfrac { 1 } { { \ sqrt 2 } } \ \ \ Leftrightarrow \ sin \ left ( { x + \ dfrac { \ pi } { 4 } } \ right ) = \ sin \ dfrac { \ pi } { 4 } \ Leftrightarrow \ left [ \ begin { array } { l } x + \ dfrac { \ pi } { 4 } = \ dfrac { \ pi } { 4 } + k2 \ pi \ \ x + \ dfrac { \ pi } { 4 } = \ dfrac { { 3 \ pi } } { 4 } + k2 \ pi \ end { array } \ right. \ Leftrightarrow \ left [ \ begin { array } { l } x = k2 \ pi \ \ x = \ dfrac { \ pi } { 2 } + k2 \ pi \ end { array } \ right. \, \, \ left ( { k \ in \ mathbb { Z } } \ right ) \ end { array } \ )
Vậy \ ( S = \ left \ { { k2 \ pi, \, \, \ dfrac { \ pi } { 2 } + k2 \ pi \, , \, \, k \ in \ mathbb { Z } } \ right \ } \ ) .Đáp án – Lời giải Câu hỏi 28 :Giải phương trình \ ( \ left ( { 1 + \ tan x } \ right ) \ left ( { 1 + \ sin 2 x } \ right ) = 1 + \ tan x. \ )

• A\(S = \left\{ { – \frac{\pi }{4} + k\pi ,\,\,\frac{{k\pi }}{2},\,\,k \in \mathbb{Z}} \right\}\)
• B\(S = \left\{ { – \frac{\pi }{4} + k\pi ,\,\,k\pi ,\,\,k \in \mathbb{Z}} \right\}\)
• C\(S = \left\{ {\frac{\pi }{4} + k\pi ,\,\,\frac{{k\pi }}{2},\,\,k \in \mathbb{Z}} \right\}\)
• D\(S = \left\{ {\frac{\pi }{4} + k\pi ,\,\,k\pi ,\,\,k \in \mathbb{Z}} \right\}\)

Đáp án: A

Lời giải cụ thể :ĐK : \ ( \ cos x \ ne 0 \ Leftrightarrow x \ ne \ frac { \ pi } { 2 } + k \ pi \, \, \ left ( { k \ in \ mathbb { Z } } \ right ) \ ) .
\ ( \ ) \ ( \ begin { array } { l } \, \, \, \, \, \, \ left ( { 1 + \ tan x } \ right ) \ left ( { 1 + \ sin 2 x } \ right ) = 1 + \ tan x. \ \ \ Leftrightarrow \ left ( { 1 + \ tan x } \ right ) \ left ( { 1 + \ sin 2 x } \ right ) – \ left ( { 1 + \ tan x } \ right ) = 0 \ \ \ Leftrightarrow \ left ( { 1 + \ tan x } \ right ) \ left ( { 1 + \ sin 2 x – 1 } \ right ) = 0 \ \ \ Leftrightarrow \ left ( { 1 + \ tan x } \ right ). sin2x = 0 \ \ \ Leftrightarrow \ left [ \ begin { array } { l } 1 + \ tan x = 0 \ \ \ sin 2 x = 0 \ end { array } \ right. \ Leftrightarrow \ left [ \ begin { array } { l } \ tan x = – 1 \ \ \ sin 2 x = 0 \ end { array } \ right. \ \ \ Leftrightarrow \ left [ \ begin { array } { l } x = \ frac { { – \ pi } } { 4 } + k \ pi \ \ 2 x = k \ pi \ end { array } \ right. \ Leftrightarrow \ left [ \ begin { array } { l } x = \ frac { { – \ pi } } { 4 } + k \ pi \, \, \ left ( { tm } \ right ) \ \ x = \ frac { { k \ pi } } { 2 } \, \, \, \, \, \, \, \, \, \, \, \, \, \ left ( { tm } \ right ) \ end { array } \ right. \, \, \ left ( { k \ in \ mathbb { Z } } \ right ) \ end { array } \ )
Vậy \ ( S = \ left \ { { – \ frac { \ pi } { 4 } + k \ pi, \, \, \ frac { { k \ pi } } { 2 }, \, \, k \ in \ mathbb { Z } } \ right \ } \ ) .

Chọn A.

Đáp án – Lời giải Câu hỏi 29 :

Giải phương trình \(\left| {\cos x – \sin x} \right| + 6\sin x\cos x = 1.\)

• A\(S = \left\{ {\dfrac{\pi }{2} + k2\pi ;\,\,k2\pi } \right\}\)
• B\(S = \left\{ {\pi  + k2\pi ;\,\,k2\pi } \right\}\)
• C\(S = \left\{ {\pi  + k\pi ;\,\,k\pi } \right\}\)
• D\(S = \left\{ {\dfrac{{k\pi }}{2};\,\,k \in \mathbb{Z}} \right\}\).

Đáp án: D

Lời giải cụ thể :\ ( \ left | { \ cos x – \ sin x } \ right | + 6 \ sin x \ cos x = 1. \ Leftrightarrow \ left | { \ sin x – \ cos x } \ right | + 6 \ sin x. \ cos x = 1 \, \, \, \ left ( * \ right ) \ )
Đặt \ ( \ sin x – \ cos x = t \, \, \, \, \ left ( { – \ sqrt 2 \ le t \ le \ sqrt 2 } \ right ) \ ), khi đó ta có :
\ ( { \ left ( { \ sin x – \ cos x } \ right ) ^ 2 } = { t ^ 2 } \ Leftrightarrow 1 – 2 \ sin x. \ cos x = { t ^ 2 } \ Leftrightarrow \ sin x. \ cos x = \ dfrac { { 1 – { t ^ 2 } } } { 2 } \ ) .
Phương trình trở thành : \ ( \ left | t \ right | + 6 \ left ( { \ dfrac { { 1 – { t ^ 2 } } } { 2 } } \ right ) = 1 \ Leftrightarrow \ left | t \ right | + 3 – 3 { t ^ 2 } = 1 \, \, \, \ left ( 1 \ right ) \ )
TH1 : \ ( 0 \ le t \ le \ sqrt 2 \ ) .
\ ( \ begin { array } { l } \ Rightarrow \ left ( 1 \ right ) \ Leftrightarrow – 3 { t ^ 2 } + t + 2 = 0 \ Leftrightarrow \ left [ \ begin { array } { l } t = \ dfrac { { – 2 } } { 3 } \, \, \, \ left ( { ktm } \ right ) \ \ t = 1 \, \, \, \, \, \, \, \, \ left ( { tm } \ right ) \ end { array } \ right. \ \ \ Leftrightarrow \ sin x – \ cos x = 1 \ Leftrightarrow \ sqrt 2 \ sin \ left ( { x – \ dfrac { \ pi } { 4 } } \ right ) = 1 \ \ \ Leftrightarrow \ sin \ left ( { x – \ dfrac { \ pi } { 4 } } \ right ) = \ dfrac { 1 } { { \ sqrt 2 } } \ Leftrightarrow \ left [ \ begin { array } { l } x – \ dfrac { \ pi } { 4 } = \ dfrac { \ pi } { 4 } + k2 \ pi \ \ x – \ dfrac { \ pi } { 4 } = \ dfrac { { 3 \ pi } } { 4 } + k2 \ pi \ end { array } \ right. \ Leftrightarrow \ left [ \ begin { array } { l } x = \ dfrac { \ pi } { 2 } + k2 \ pi \ \ x = \ pi + k2 \ pi \ end { array } \ right. \, \, \ left ( { k \ in \ mathbb { Z } } \ right ) \ end { array } \ )
TH2 : \ ( – \ sqrt 2 \ le t < 0 \ ) . \ ( \ begin { array } { l } \ Rightarrow \ left ( 1 \ right ) \ Leftrightarrow - 3 { t ^ 2 } - t + 2 = 0 \ Leftrightarrow \ left [ \ begin { array } { l } t = \ dfrac { 2 } { 3 } \, \, \, \ left ( { ktm } \ right ) \ \ t = - 1 \, \, \ left ( { tm } \ right ) \ end { array } \ right. \ \ \ Leftrightarrow \ sin x - \ cos x = - 1 \ Leftrightarrow \ sqrt 2 \ sin \ left ( { x - \ dfrac { \ pi } { 4 } } \ right ) = - 1 \ \ \ Leftrightarrow sin \ left ( { x - \ dfrac { \ pi } { 4 } } \ right ) = \ dfrac { { - 1 } } { { \ sqrt 2 } } \ Leftrightarrow \ left [ \ begin { array } { l } x - \ dfrac { \ pi } { 4 } = - \ dfrac { \ pi } { 4 } + k2 \ pi \ \ x - \ dfrac { \ pi } { 4 } = \ dfrac { { 5 \ pi } } { 4 } + k2 \ pi \ end { array } \ right. \ Leftrightarrow \ left [ \ begin { array } { l } x = k2 \ pi \ \ x = \ dfrac { { 3 \ pi } } { 2 } + k2 \ pi \ end { array } \ right. \, \, \ left ( { k \ in \ mathbb { Z } } \ right ) \ end { array } \ ) Vậy \ ( S = \ left \ { { \ dfrac { { k \ pi } } { 2 } ; \, \, k \ in \ mathbb { Z } } \ right \ } \ ) .Đáp án - Lời giải Câu hỏi 30 :

Giải phương trình \(\cos x\sin x + \left| {\cos x + \sin x} \right| = 1.\)

• A\(S = \left\{ {\frac{\pi }{2} + k\pi ;\,\,\pi  + k\pi } \right\}\)
• B\(S = \left\{ {\dfrac{{k\pi }}{2},\,\,k \in \mathbb{Z}} \right\}.\)
• C\(S = \left\{ {\frac{\pi }{2} + k2\pi ;\,\,k2\pi } \right\}\)
• D\(S = \left\{ {\frac{\pi }{2} + k\pi ;\,\,\,k\pi } \right\}\)

Đáp án: B

Lời giải chi tiết cụ thể :\ ( \ cos x \ sin x + \ left | { \ cos x + \ sin x } \ right | = 1 \ Leftrightarrow \ cos x \ sin x + \ left | { \ sin x + \ cos x } \ right | = 1 \, \, \ left ( 1 \ right ) \ )
Đặt \ ( \ left | { \ sin x + \ cos x } \ right | = t \, \, \, \, \ left ( { 0 \ le t \ le \ sqrt 2 } \ right ) \ ), khi đó ta có :
\ ( { \ left ( { \ sin x + \ cos x } \ right ) ^ 2 } = { t ^ 2 } \ Leftrightarrow 1 + 2 \ sin x.cosx = { t ^ 2 } \ Leftrightarrow \ sin x.cosx = \ dfrac { { { t ^ 2 } – 1 } } { 2 } \ )
Khi đó phương trình trở thành : \ ( \ dfrac { { { t ^ 2 } – 1 } } { 2 } + t = 1 \ Leftrightarrow { t ^ 2 } + 2 t – 3 = 0 \ Leftrightarrow \ left [ \ begin { array } { l } t = 1 \, \, \, \, \, \, \, \ left ( { tm } \ right ) \ \ t = – 3 \, \, \ left ( { ktm } \ right ) \ end { array } \ right. \ )
\ ( \ begin { array } { l } \ Rightarrow \ left | { \ sin x + \ cos x } \ right | = 1 \ Leftrightarrow \ left [ \ begin { array } { l } \ sin x + \ cos x = 1 \ \ \ sin x + \ cos x = – 1 \ end { array } \ right. \ \ \ Leftrightarrow \ left [ \ begin { array } { l } \ sqrt 2 \ sin \ left ( { x + \ dfrac { \ pi } { 4 } } \ right ) = 1 \ \ \ sqrt 2 \ sin \ left ( { x + \ dfrac { \ pi } { 4 } } \ right ) = – 1 \ end { array } \ right. \ Leftrightarrow \ left [ \ begin { array } { l } \ sin \ left ( { x + \ dfrac { \ pi } { 4 } } \ right ) = \ dfrac { 1 } { { \ sqrt 2 } } \ \ \ sin \ left ( { x + \ dfrac { \ pi } { 4 } } \ right ) = – \ dfrac { 1 } { { \ sqrt 2 } } \ end { array } \ right. \ \ \ Leftrightarrow \ left [ \ begin { array } { l } x + \ dfrac { \ pi } { 4 } = \ dfrac { \ pi } { 4 } + k2 \ pi \ \ x + \ dfrac { \ pi } { 4 } = \ dfrac { { 3 \ pi } } { 4 } + k2 \ pi \ \ x + \ dfrac { \ pi } { 4 } = – \ dfrac { \ pi } { 4 } + k2 \ pi \ \ x + \ dfrac { \ pi } { 4 } = \ dfrac { { 5 \ pi } } { 4 } + k2 \ pi \ end { array } \ right. \ Leftrightarrow \ left [ \ begin { array } { l } x = k2 \ pi \ \ x = \ dfrac { \ pi } { 2 } + k2 \ pi \ \ x = – \ dfrac { \ pi } { 2 } + k2 \ pi \ \ x = \ pi + k2 \ pi \ end { array } \ right. \ Leftrightarrow x = \ dfrac { { k \ pi } } { 2 } \, \, \ left ( { k \ in \ mathbb { Z } } \ right ) \ end { array } \ )
Vậy \ ( S = \ left \ { { \ dfrac { { k \ pi } } { 2 }, \, \, k \ in \ mathbb { Z } } \ right \ }. \ )Đáp án – Lời giải Câu hỏi 31 :

Giải phương trình \(4\sin x\cos x + 1 = \cos x – \sin x.\)

• A\(S = \left\{ {k2\pi ;\frac{{3\pi }}{2} + k2\pi } \right\}\)
• B\(S = \left\{ {k\pi ;\frac{{3\pi }}{2} + k\pi } \right\}\)
• C\(S = \left\{ {k\pi ;\frac{\pi }{2} + k\pi } \right\}\)
• D\(S = \left\{ {k2\pi ;\frac{\pi }{2} + k2\pi } \right\}\)

Đáp án: A

Lời giải cụ thể :\ ( 4 \ sin x. \ cos x + 1 = \ cos x – \ sin x \ Leftrightarrow \ sin x – \ cos x + 4 \ sin x. \ cos x + 1 = 0 \, \, \, \ left ( * \ right ) \ )
Đặt \ ( \ sin x – \ cos x = t \, \, \, \, \ left ( { – \ sqrt 2 \ le t \ le \ sqrt 2 } \ right ) \ ), khi đó ta có :
\ ( { \ left ( { \ sin x – \ cos x } \ right ) ^ 2 } = { t ^ 2 } \ Leftrightarrow 1 – 2 \ sin x. \ cos x = { t ^ 2 } \ Leftrightarrow \ sin x. \ cos x = \ dfrac { { 1 – { t ^ 2 } } } { 2 } \ ) .
Phương trình trở thành :
\ ( \ begin { array } { l } \ Rightarrow ( * ) \ Leftrightarrow t + 4 \ left ( { \ dfrac { { 1 – { t ^ 2 } } } { 2 } } \ right ) + 1 = 0 \ Leftrightarrow – 2 { t ^ 2 } + t + 3 = 0 \ Leftrightarrow \ left [ \ begin { array } { l } t = \ dfrac { 3 } { 2 } \, \, \, \ left ( { ktm } \ right ) \ \ t = – 1 \, \, \ left ( { tm } \ right ) \ end { array } \ right. \ \ t = – 1 \ Leftrightarrow \ sin x – \ cos x = – 1 \ Leftrightarrow \ sqrt 2 \ sin \ left ( { x – \ dfrac { \ pi } { 4 } } \ right ) = – 1 \ \ \ Leftrightarrow \ sin \ left ( { x – \ dfrac { \ pi } { 4 } } \ right ) = \ sin \ left ( { \ dfrac { { – \ pi } } { 4 } } \ right ) \ Leftrightarrow \ left [ \ begin { array } { l } x – \ dfrac { \ pi } { 4 } = – \ dfrac { \ pi } { 4 } + k2 \ pi \ \ x – \ dfrac { \ pi } { 4 } = \ dfrac { { 5 \ pi } } { 4 } + k2 \ pi \ end { array } \ right. \ Leftrightarrow \ left [ \ begin { array } { l } x = k2 \ pi \ \ x = \ dfrac { { 3 \ pi } } { 2 } + k2 \ pi \ end { array } \ right. \, \, \ left ( { k \ in \ mathbb { Z } } \ right ) \ end { array } \ )
Vậy \ ( S = \ left \ { { k2 \ pi ; \ dfrac { { 3 \ pi } } { 2 } + k2 \ pi, \, \, k \ in \ mathbb { Z } } \ right \ }. \ )Đáp án – Lời giải Câu hỏi 32 :

Giải phương trình \({\tan ^2}x + {\cot ^2}x + 2\tan x + 2\cot x = 6.\)

• A\(S = \left\{ {\dfrac{\pi }{4} + k\pi ,\,\,\dfrac{{ – \pi }}{{12}} + k\pi ;\,\,\dfrac{{ – 5\pi }}{{12}} + k\pi ,\,\,k \in \mathbb{Z}} \right\}\).
• B\(S = \left\{ {-\dfrac{\pi }{4} + k\pi ,\,\,\dfrac{{ – \pi }}{{12}} + k\pi ;\,\,\dfrac{{ – 5\pi }}{{12}} + k\pi ,\,\,k \in \mathbb{Z}} \right\}\).
• C\(S = \left\{ {\dfrac{\pi }{4} + k\pi ,\,\,\dfrac{{ \pi }}{{12}} + k\pi ;\,\,\dfrac{{ – 5\pi }}{{12}} + k\pi ,\,\,k \in \mathbb{Z}} \right\}\).
• D\(S = \left\{ {\dfrac{\pi }{4} + k\pi ,\,\,\dfrac{{ \pi }}{{12}} + k\pi ;\,\,\dfrac{{ 5\pi }}{{12}} + k\pi ,\,\,k \in \mathbb{Z}} \right\}\).

Đáp án: A

Lời giải cụ thể :\ ( \ begin { array } { l } \, \, \, \, \, { \ tan ^ 2 } x + { \ cot ^ 2 } x + 2 \ tan x + 2 cotx = 6 \, \, \, \ left ( { x \ ne \ dfrac { { k \ pi } } { 2 }, \, \, k \ in \ mathbb { Z } } \ right ) \ \ \ Rightarrow { \ tan ^ 2 } x + \ dfrac { 1 } { { { { \ tan } ^ 2 } x } } + 2 \ left ( { \ tan x + \ dfrac { 1 } { { \ tan x } } } \ right ) = 6 \ end { array } \ )
Đặt \ ( \ tan x + \ dfrac { 1 } { { \ tan x } } = t \ Leftrightarrow { \ tan ^ 2 } x + \ dfrac { 1 } { { { { \ tan } ^ 2 } x } } + 2 \ tan x. \ dfrac { 1 } { { \ tan x } } = { t ^ 2 } \ Leftrightarrow { \ tan ^ 2 } x + \ dfrac { 1 } { { { { \ tan } ^ 2 } x } } = { t ^ 2 } – 2 \ )
Thế vào phương trình ta có :
\ ( \ begin { array } { l } { t ^ 2 } – 2 + 2 t = 6 \ Leftrightarrow { t ^ 2 } + 2 t – 8 = 0 \ Leftrightarrow \ left [ \ begin { array } { l } t = 2 \ \ t = – 4 \ end { array } \ right. \ \ + ) \, \, t = 2 \ Leftrightarrow \ tan x + \ dfrac { 1 } { { \ tan x } } = 2 \ Leftrightarrow { \ tan ^ 2 } x – 2 \ tan x + 1 = 0 \ \ \ Leftrightarrow \ tan x = 1 \ Leftrightarrow x = \ dfrac { \ pi } { 4 } + k \ pi \, \, \, \ left ( { k \ in \ mathbb { Z } } \ right ) \, \, \ left ( { tm } \ right ) \ \ + ) \, \, \, t = – 4 \ Leftrightarrow \ tan x + \ dfrac { 1 } { { \ tan x } } = – 4 \ Leftrightarrow { \ tan ^ 2 } x + 4 \ tan x + 1 = 0 \ \ \ Leftrightarrow \ left [ \ begin { array } { l } { \ mathop { \ rm tanx } \ nolimits } = – 2 + \ sqrt 3 \ Leftrightarrow x = \ dfrac { { – \ pi } } { { 12 } } + k \ pi \ \ { \ mathop { \ rm tanx } \ nolimits } = – 2 – \ sqrt 3 \ Leftrightarrow x = \ dfrac { { – 5 \ pi } } { { 12 } } + k \ pi \ end { array } \ right. \ left ( { k \ in \ mathbb { Z } } \ right ) \, \, \ left ( { tm } \ right ) \ end { array } \ )
Vậy \ ( S = \ left \ { { \ dfrac { \ pi } { 4 } + k \ pi, \, \, \ dfrac { { – \ pi } } { { 12 } } + k \ pi ; \, \, \ dfrac { { – 5 \ pi } } { { 12 } } + k \ pi, \, \, k \ in \ mathbb { Z } } \ right \ } \ ) .Đáp án – Lời giải Câu hỏi 33 :

Giải phương trình \(\sqrt 2 \left( {\sin x + \cos x} \right) – 1 = \sin x\cos x.\)

• A\(S = \left\{ {\alpha  – \frac{\pi }{4} + k\pi ;\frac{{3\pi }}{4} – \alpha  + k\pi } \right\}\)
• B\(S = \left\{ {\alpha  – \frac{\pi }{4} + k2\pi ;\frac{{3\pi }}{4} – \alpha  + k2\pi } \right\}\)
• C\(S = \left\{ {\alpha  – \frac{\pi }{4} + k2\pi ;\alpha  – \frac{{3\pi }}{4} + k2\pi } \right\}\)
• D\(S = \left\{ {\alpha  – \frac{\pi }{4} + k\pi ;\alpha  – \frac{{3\pi }}{4} + k\pi } \right\}\)

Đáp án: B

Lời giải chi tiết cụ thể :\ ( \ sqrt 2 \ left ( { \ sin x + cosx } \ right ) – 1 = \ sin x.cosx \, \, \, \ left ( * \ right ) \ )
Đặt, \ ( \ sin x + \ cos x = t \, \, \, \, \ left ( { – \ sqrt 2 \ le t \ le \ sqrt 2 } \ right ) \ ) khi đó ta có :

\(\begin{array}{l}{\left( {\sin x + cosx} \right)^2} = {t^2} \Leftrightarrow {\sin ^2}x + 2\sin x.\cos x + {\cos ^2}x = {t^2}\\ \Leftrightarrow 1 + 2\sin x.\cos x = {t^2} \Leftrightarrow \sin x.\cos x = \dfrac{{{t^2} – 1}}{2}\end{array}\)
Phương trình trở thành:

\(\begin{array}{l}
\Rightarrow \sqrt 2 t – 1 = \frac{{{t^2} – 1}}{2} \Leftrightarrow {t^2} – 2\sqrt 2 t + 1 = 0 \Leftrightarrow \left[ \begin{array}{l}
t = 1 + \sqrt 2 \,\,\,\,\,\left( {ktm} \right)\\
t = – 1 + \sqrt 2 \,\,\left( {tm} \right)
\end{array} \right.\\
\Leftrightarrow \sin x + \cos x = – 1 + \sqrt 2 \\
\Leftrightarrow \sin \left( {x + \frac{\pi }{4}} \right) = \sin \alpha \,\,\,\,\,\left( {Voi\,\,\sin \alpha = \frac{{ – 1 + \sqrt 2 }}{{\sqrt 2 }}} \right)\\
\Leftrightarrow \left[ \begin{array}{l}
x + \frac{\pi }{4} = \alpha + k2\pi \\
x + \frac{\pi }{4} = \pi – \alpha + k2\pi
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
x = \alpha – \frac{\pi }{4} + k2\pi \\
x = \frac{{3\pi }}{4} – \alpha + k2\pi
\end{array} \right.\left( {k \in } \right)
\end{array}\)

Đáp án – Lời giải Câu hỏi 34 :\ ( 7 \ cos x = 4 { \ cos ^ 3 } x + 4 \ sin 2 x. \ )

• A\(\left[ \begin{array}{l}x = \frac{\pi }{2} + k2\pi \\x = \frac{\pi }{6} + k2\pi \\x = \frac{{5\pi }}{6} + k2\pi \end{array} \right.\left( {k \in Z} \right)\)
• B\(\left[ \begin{array}{l}x = \frac{\pi }{2} + k\pi \\x = \frac{\pi }{6} + k\pi \\x = \frac{{5\pi }}{6} + k\pi \end{array} \right.\left( {k \in Z} \right)\)
• C\(\left[ \begin{array}{l}x =  – \frac{\pi }{2} + k2\pi \\x =  – \frac{\pi }{6} + k2\pi \\x = \frac{{5\pi }}{6} + k2\pi \end{array} \right.\left( {k \in Z} \right)\)
• D\(\left[ \begin{array}{l}x =  – \frac{\pi }{2} + k\pi \\x =  – \frac{\pi }{6} + k\pi \\x = \frac{{5\pi }}{6} + k\pi \end{array} \right.\left( {k \in Z} \right)\)

Đáp án: B

Lời giải cụ thể :\ ( \ begin { array } { l } 7 \ cos x = 4 { \ cos ^ 3 } x + 4 \ sin 2 x \ \ \ Leftrightarrow 7 \ cos x – 4 { \ cos ^ 3 } x – 8 \ sin x. \ cos x = 0 \ \ \ Leftrightarrow \ cos x \ left ( { 7 – 4 { { \ cos } ^ 2 } x – 8 \ sin x } \ right ) = 0 \ \ \ Leftrightarrow \ left [ \ begin { array } { l } \ cos x = 0 \ \ 7 – 4 { \ cos ^ 2 } x – 8 \ sin x = 0 \ end { array } \ right. \ \ \ Leftrightarrow \ left [ \ begin { array } { l } x = \ frac { \ pi } { 2 } + k \ pi \ \ 7 – 4 \ left ( { 1 – { { \ sin } ^ 2 } x } \ right ) – 8 \ sin x = 0 \ end { array } \ right. \ \ \ Leftrightarrow \ left [ \ begin { array } { l } x = \ frac { \ pi } { 2 } + k \ pi \ \ \ sin x = \ frac { 3 } { 2 } ( L ) \ \ \ sin x = \ frac { 1 } { 2 } ( TM ) \ end { array } \ right. \ \ \ Leftrightarrow \ left [ \ begin { array } { l } x = \ frac { \ pi } { 2 } + k \ pi \ \ x = \ frac { \ pi } { 6 } + k \ pi \ \ x = \ frac { { 5 \ pi } } { 6 } + k \ pi \ end { array } \ right. \ left ( { k \ in Z } \ right ) \ end { array } \ )

Chọn B.

Đáp án – Lời giải Câu hỏi 35 :\ ( { \ cos ^ 3 } x + 2 \ sin x { \ cos ^ 2 } x – 3 { \ sin ^ 3 } x = 0. \ )

• A\(x = \frac{\pi }{4} + k\pi \left( {k \in Z} \right)\)
• B\(x = \frac{\pi }{4} + k2\pi \left( {k \in Z} \right)\)
• C\(x =  – \frac{\pi }{4} + k\pi \left( {k \in Z} \right)\)
• D\(x =  – \frac{\pi }{4} + k2\pi \left( {k \in Z} \right)\)

Đáp án: A

Lời giải cụ thể :\ ( { \ cos ^ 3 } x + 2 { \ mathop { \ rm sinx } \ nolimits }. co { s ^ 2 } x – 3 { \ sin ^ 3 } x = 0 ( 1 ) \ )
+ Xét \ ( \ cos x = 0 \ Rightarrow ( 1 ) \ Leftrightarrow { \ mathop { \ rm sinx } \ nolimits } = 0 ( L ) \ )
+ Xét \ ( \ cos x \ ne 0 \ )
Chia 2 vế của ( 1 ) cho \ ( { \ cos ^ 3 } x \ )
\ ( \ begin { array } { l } \ Rightarrow ( 1 ) \ Leftrightarrow 1 + 2 { \ mathop { \ rm tanx } \ nolimits } – 3 ta { n ^ 3 } x = 0 \ \ \ Leftrightarrow { \ mathop { \ rm tanx } \ nolimits } = 1 \ \ \ Leftrightarrow x = \ frac { \ pi } { 4 } + k \ pi \ left ( { k \ in Z } \ right ) \ end { array } \ )

Chọn A.

Đáp án – Lời giải Câu hỏi 36 :\ ( 3 { \ cos ^ 4 } x – 4 { \ sin ^ 2 } x { \ cos ^ 2 } x + { \ sin ^ 4 } x = 0. \ )

• A\(\left[ \begin{array}{l}x = \frac{{2\pi }}{3} + k2\pi \\x = \frac{\pi }{3} + k2\pi \\x = \frac{\pi }{4} + k2\pi \\x = \frac{{3\pi }}{4} + k2\pi \end{array} \right.\,\,\,\,\left( {k \in \mathbb{Z}} \right)\)
• B\(\left[ \begin{array}{l}
  x = \frac{{2\pi }}{3} + k\pi \\
  x = \frac{\pi }{4} + k\pi
  \end{array} \right.\)
• C\(\left[ \begin{array}{l}x = \frac{{2\pi }}{3} + k2\pi \\x = \frac{\pi }{3} + k2\pi \\x =  – \frac{\pi }{4} + k2\pi \\x = \frac{{5\pi }}{4} + k2\pi \end{array} \right.\,\,\,\,\left( {k \in \mathbb{Z}} \right)\)
• D\(\left[ \begin{array}{l}x = \frac{{2\pi }}{3} + k\pi \\x = \frac{\pi }{3} + k\pi \\x = \frac{\pi }{4} + k\pi \\x = \frac{{3\pi }}{4} + k\pi \end{array} \right.\,\,\,\,\left( {k \in \mathbb{Z}} \right)\)

Đáp án: D

Lời giải chi tiết cụ thể :\ ( 3 { \ cos ^ 4 } x – 4 { \ sin ^ 2 } x. { \ cos ^ 2 } x + { \ sin ^ 4 } x = 0 \ )
+ Xét \ ( \ cos x = 0 \ Rightarrow { \ sin ^ 4 } x = 0 \ Leftrightarrow x = 0 \ )
+ Xét \ ( \ cos x \ ne 0 \ ). Chia cả 2 vế cho \ ( { \ cos ^ 4 } x \ )
\ ( \ begin { array } { l } 3 – 4 { \ tan ^ 2 } x + { \ tan ^ 4 } x = 0 \ \ \ Leftrightarrow \ left [ \ begin { array } { l } { \ tan ^ 2 } x = 3 \ \ { \ tan ^ 2 } x = 1 \ end { array } \ right. \ Leftrightarrow \ left [ \ begin { array } { l } x = \ frac { { 2 \ pi } } { 3 } + k \ pi \ \ x = \ frac { \ pi } { 3 } + k \ pi \ \ x = \ frac { \ pi } { 4 } + k \ pi \ \ x = \ frac { { 3 \ pi } } { 4 } + k \ pi \ end { array } \ right. \, \, \, \, \ left ( { k \ in \ mathbb { Z } } \ right ) \ end { array } \ )

Chọn D.

Đáp án – Lời giải Câu hỏi 37 :Giải phương trình : \ ( { \ sin ^ 4 } x + { \ sin ^ 4 } \ left ( { x + \ dfrac { \ pi } { 4 } } \ right ) + { \ cos ^ 4 } \ left ( { x + \ dfrac { \ pi } { 4 } } \ right ) = \ dfrac { 9 } { 8 } \ )

• A\(x =  \dfrac{1}{2}\arccos \dfrac{{ – 2 + \sqrt 6 }}{2} + k\pi \)
• B\(x =  \pm \dfrac{1}{2}\arccos \dfrac{{ – 2 + \sqrt 6 }}{2} + k\pi \)
• C\(x = – \dfrac{1}{2}\arccos \dfrac{{ – 2 + \sqrt 6 }}{2} + k\pi \)
• D\(x =  \pm \dfrac{1}{2}\arccos \dfrac{{ – 2 + \sqrt 6 }}{2} + k2\pi \)

Đáp án: B

Lời giải chi tiết cụ thể :\ ( \ begin { array } { l } { \ sin ^ 4 } x + { \ sin ^ 4 } \ left ( { x + \ dfrac { \ pi } { 4 } } \ right ) + { \ cos ^ 4 } \ left ( { x + \ dfrac { \ pi } { 4 } } \ right ) = \ dfrac { 9 } { 8 } \ \ \ Leftrightarrow { \ sin ^ 4 } x + { \ left [ { \ dfrac { 1 } { { \ sqrt 2 } } \ left ( { \ sin \, x + \ cos x } \ right ) } \ right ] ^ 4 } + { \ left [ { – \ dfrac { 1 } { { \ sqrt 2 } } \ left ( { \ sin \, x – \ cos x } \ right ) } \ right ] ^ 4 } = \ dfrac { 9 } { 8 } \ \ \ Leftrightarrow 4 { \ sin ^ 4 } x + { \ left ( { \ sin \, x + \ cos x } \ right ) ^ 4 } + { \ left ( { \ sin \, x – \ cos x } \ right ) ^ 4 } = \ dfrac { 9 } { 2 } \ \ \ Leftrightarrow 4 { \ sin ^ 4 } x + { \ left [ { { { \ left ( { \ sin \, x + \ cos x } \ right ) } ^ 2 } } \ right ] ^ 2 } + { \ left [ { { { \ left ( { \ sin \, x – \ cos x } \ right ) } ^ 2 } } \ right ] ^ 2 } = \ dfrac { 9 } { 2 } \ \ \ Leftrightarrow 4 { \ sin ^ 4 } x + { \ left ( { 1 + \ sin 2 x } \ right ) ^ 2 } + { \ left ( { 1 – \ sin 2 x } \ right ) ^ 2 } = \ dfrac { 9 } { 2 } \ \ \ Leftrightarrow 4 { \ sin ^ 4 } x + 2 { \ sin ^ 2 } 2 x – \ dfrac { 5 } { 2 } = 0 \ \ \ Leftrightarrow 4 { \ sin ^ 4 } x + 8 { \ sin ^ 2 } x. { \ cos ^ 2 } x – \ dfrac { 5 } { 2 } = 0 \ end { array } \ )
Đặt \ ( { \ sin ^ 2 } x = t \, \, \, \, \ left ( { \ left | t \ right | \ le 1 } \ right ) \ )
\ ( \ begin { array } { l } 4 { t ^ 2 } – 8 t \ left ( { 1 – t } \ right ) – \ dfrac { 5 } { 2 } = 0 \ Leftrightarrow – 4 { t ^ 2 } + 8 t – \ dfrac { 5 } { 2 } = 0 \ Leftrightarrow \ left [ \ begin { array } { l } t = \ dfrac { { 4 + \ sqrt 6 } } { 4 } \, \, \, \ left ( { ktm } \ right ) \ \ t = \ dfrac { { 4 – \ sqrt 6 } } { 4 } \, \, \, \ left ( { tm } \ right ) \ end { array } \ right. \ \ \ Leftrightarrow { \ sin ^ 2 } x = \ dfrac { { 4 – \ sqrt 6 } } { 4 } \ Leftrightarrow \ dfrac { 1 } { 2 } \ left ( { 1 – \ cos 2 x } \ right ) = \ dfrac { { 4 – \ sqrt 6 } } { 4 } \ \ \ Leftrightarrow \ cos 2 x = \ dfrac { { – 2 + \ sqrt 6 } } { 2 } \ Leftrightarrow x = \ pm \ dfrac { 1 } { 2 } \ arccos \ dfrac { { – 2 + \ sqrt 6 } } { 2 } + k \ pi \, \, \ left ( { k \ in \ mathbb { Z } } \ right ) \ end { array } \ )Đáp án – Lời giải Câu hỏi 38 :

Giải phương trình \(\left( {2\sin x – 1} \right)\left( {2\cos 2x + 2\sin x + 1} \right) = 3 – 4{\cos ^2}x\)

• A\(S = \left\{ {\frac{\pi }{4} + \frac{{k\pi }}{2};\frac{\pi }{6} + k2\pi ,\frac{{5\pi }}{6} + k2\pi ,\,\,\kappa  \in \mathbb{Z}} \right\}\)
• B\(S = \left\{ {\frac{\pi }{2} + \frac{{k\pi }}{2};\frac{\pi }{6} + k2\pi ,\frac{{5\pi }}{6} + k2\pi ,\,k \in \mathbb{Z}} \right\}\)
• C\(S = \left\{ {\frac{\pi }{4} + \frac{{k\pi }}{2};\frac{\pi }{3} + k2\pi ,\frac{{2\pi }}{3} + k2\pi ,\,\,\kappa  \in \mathbb{Z}} \right\}\)
• D\(S = \left\{ {\frac{\pi }{2} + \frac{{k\pi }}{2};\frac{\pi }{3} + k2\pi ,\frac{{2\pi }}{3} + k2\pi ,\,\,\kappa  \in \mathbb{Z}} \right\}\)

Đáp án: A

Lời giải cụ thể :

\ ( \ begin { array } { l } \, \, \, \, \, \, \ left ( { 2 \ sin x – 1 } \ right ) \ left ( { 2 \ cos 2 x + 2 \ sin x + 1 } \ right ) = 3 – 4 { \ cos ^ 2 } x \ \ \ Leftrightarrow \ left ( { 2 \ sin x – 1 } \ right ) \ left ( { 2 – 4 { { \ sin } ^ 2 } x + 2 \ sin x + 1 } \ right ) = 3 – 4 { \ cos ^ 2 } x \ \ \ Leftrightarrow \ left ( { 2 \ sin x – 1 } \ right ) \ left ( { – 4 { { \ sin } ^ 2 } x + 2 \ sin x + 3 } \ right ) = 3 – 4 { \ cos ^ 2 } x \ \ \ Leftrightarrow – 8 { \ sin ^ 3 } x + 4 { \ sin ^ 2 } x + 6 \ sin x + 4 { \ sin ^ 2 } x – 2 \ sin x – 3 = 3 – 4 { \ cos ^ 2 } x \ \ \ Leftrightarrow – 8 { \ sin ^ 3 } x + 8 { \ sin ^ 2 } x + 4 \ sin x – 3 = 3 – 4 \ left ( { 1 – { { \ sin } ^ 2 } x } \ right ) \ \ \ Leftrightarrow – 8 { \ sin ^ 3 } x + 8 { \ sin ^ 2 } x + 4 \ sin x – 3 = 3 – 4 + 4 { \ sin ^ 2 } x \ \ \ Leftrightarrow – 8 { \ sin ^ 3 } x + 4 { \ sin ^ 2 } x + 4 \ sin x – 2 = 0 \ \ \ Leftrightarrow \ left [ \ begin { array } { l } \ sin x = \ frac { { \ sqrt 2 } } { 2 } \ \ \ sin x = – \ frac { { \ sqrt 2 } } { 2 } \ \ \ sin x = \ frac { 1 } { 2 } \ end { array } \ right. \ Leftrightarrow \ left [ \ begin { array } { l } x = \ frac { \ pi } { 4 } + k2 \ pi \ \ x = \ frac { { 3 \ pi } } { 4 } + k2 \ pi \ \ x = \ frac { { – \ pi } } { 4 } + k2 \ pi \ \ x = \ frac { { 5 \ pi } } { 4 } + k2 \ pi \ \ x = \ frac { \ pi } { 6 } + k2 \ pi \ \ x = \ frac { { 5 \ pi } } { 6 } + k2 \ pi \ end { array } \ right. \, \, \, \ left ( { k \ in \ mathbb { Z } } \ right ) \ end { array } \ )
Hợp nghiệm \ ( \ Rightarrow S = \ left \ { { \ frac { \ pi } { 4 } + \ frac { { k \ pi } } { 2 } ; \ frac { \ pi } { 6 } + k2 \ pi, \ frac { { 5 \ pi } } { 6 } + k2 \ pi, \, \, \ kappa \ in \ mathbb { Z } } \ right \ } \ ) .

Chọn A.

Đáp án – Lời giải Câu hỏi 39 :Cho phương trình \ ( \ left ( { 2 m + 1 } \ right ) { \ rm { co } } { { \ rm { s } } ^ 2 } 2 x – \ left ( { 3 m – 1 } \ right ) \ sin 2 x – 3 m + 1 = 0 \ ) ( \ ( m \ ) là tham số thực ). Có tổng thể bao nhiêu giá trị nguyên của \ ( m \ ) để phương trình có đúng hai nghiệm phân biệt thuộc \ ( \ left ( { – \ pi ; \ pi } \ right ) \ ) .

• A2
• B4
• C5
• D3

Đáp án: B

Phương pháp giải :Đặt ẩn phụ, tìm nghiệm phương trình bậc 2 rồi tìm m .Lời giải cụ thể :Ta có \ ( \ left ( { 2 m + 1 } \ right ) { \ rm { co } } { { \ rm { s } } ^ 2 } 2 x – \ left ( { 3 m – 1 } \ right ) \ sin 2 x – 3 m + 1 = 0 \, \, \ left ( * \ right ) \ ) .
Đặt \ ( t = \ sin 2 x \ Rightarrow – 1 \ le t \ le 1 \ left ( { x \ in \ left ( { – \ pi ; \ pi } \ right ) } \ right ) \ )
Khi đó phương trình ( * ) có dạng :
\ ( \ begin { array } { l } \ left ( { 2 m + 1 } \ right ) \ left ( { 1 – { t ^ 2 } } \ right ) – \ left ( { 3 m – 1 } \ right ) t – 3 m + 1 = 0 \ \ \ Leftrightarrow \ left ( { 2 m + 1 } \ right ) { t ^ 2 } + \ left ( { 3 m – 1 } \ right ) t + m – 2 = 0 \ \ \ Leftrightarrow \ left ( { t + 1 } \ right ) \ left ( { \ left ( { 2 m + 1 } \ right ) t + m – 2 } \ right ) = 0 \ \ \ Leftrightarrow \ left [ \ begin { array } { l } t = – 1 \ \ \ left ( { 2 m + 1 } \ right ) t + m – 2 = 0 \ end { array } \ right. \ end { array } \ )
Nếu : \ ( t = – 1 \, \, \, \ left ( { tm } \ right ) \ Rightarrow \ sin 2 x = – 1 \ )
\ ( \ begin { array } { l } \ Leftrightarrow 2 x = \ dfrac { { – \ pi } } { 2 } + k2 \ pi \ left ( { k \ in { \ rm Z } } \ right ) \ \ \ Leftrightarrow x = \ dfrac { { – \ pi } } { 4 } + k \ pi \ in \ left ( { – \ pi ; \ pi } \ right ) \ \ \ Rightarrow \ dfrac { { – 3 } } { 4 } < k < \ dfrac { 5 } { 4 } \ Rightarrow k \ in \ left \ { { 0 ; 1 } \ right \ } \ end { array } \ ) Khi đó phương trình ( * ) có 2 nghiệm phân biệt là \ ( \ dfrac { { - \ pi } } { 4 } ; \ dfrac { { 3 \ pi } } { 4 } \ ) + ) \ ( \ left ( { 2 m + 1 } \ right ) t = 2 - m \, \, \ left ( 1 \ right ) \ ) . Nếu \ ( m = \ dfrac { { - 1 } } { 2 } ; ( 1 ) \ Rightarrow m = 2 \, \, \ left ( { ktm } \ right ) \ ) \ ( \ Rightarrow m \ ne \ dfrac { { - 1 } } { 2 } \ Rightarrow t = \ dfrac { { 2 - m } } { { 2 m + 1 } } \ ) Để phương trình ( * ) có 2 nghiệm phân biệt thì \ ( \ left [ \ begin { array } { l } t = \ dfrac { { 2 - m } } { { 2 m + 1 } } = - 1 \ \ t < - 1 \ \ t > 1 \ end { array } \ right. \ Leftrightarrow \ left [ \ begin { array } { l } m = – 3 \ \ \ dfrac { { m + 3 } } { { 2 m + 1 } } < 0 \ Leftrightarrow - 3 < m < \ dfrac { { - 1 } } { 2 } \ Leftrightarrow m \ in \ left \ { { - 2 ; - 1 } \ right \ } \ \ \ dfrac { { 3 m - 1 } } { { 2 m + 1 } } < 0 \ Leftrightarrow \ dfrac { { - 1 } } { 2 } < m < \ dfrac { 1 } { 3 } \ Leftrightarrow m = 0 \ end { array } \ right. \ ) Vậy có 4 giá trị của \ ( m \ ) thỏa mãn nhu cầu .

Chọn B.

Đáp án – Lời giải Câu hỏi 40 :Có bao nhiêu giá trị nguyên của \ ( m \ ) nhỏ hơn \ ( 2018 \ ) để phương trình \ ( \ dfrac { 3 } { { { { \ sin } ^ 2 } x } } + 3 { \ tan ^ 2 } x + \ tan x + \ cot x = m \ ) có nghiệm ?

• A\(2000\)
• B\(2001\)
• C\(2010\)
• D\(2011\)

Đáp án: D

Phương pháp giải :- Sử dụng công thức \ ( \ dfrac { 1 } { { { { \ sin } ^ 2 } x } } = 1 + { \ cot ^ 2 } x \ ) .
– \ ( t = \ tan x + \ cot x \, \, \ left ( { \ left | t \ right | \ ge 2 } \ right ) \ Rightarrow { \ tan ^ 2 } x + { \ cot ^ 2 } x = { t ^ 2 } – 2 \ ) .
– Cô lập \ ( m \ ), lập BBT của vế còn lại và Tóm lạiLời giải cụ thể :ĐK : \ ( \ left \ { \ begin { array } { l } \ sin x \ ne 0 \ \ \ cos x \ ne 0 \ end { array } \ right. \ Leftrightarrow \ sin 2 x \ ne 0 \ Leftrightarrow 2 x \ ne k \ pi \ Leftrightarrow x \ ne \ dfrac { { k \ pi } } { 2 } \, \, \ left ( { k \ in \ mathbb { Z } } \ right ) \ ) .
\ ( \ begin { array } { l } \, \, \, \, \, \, \ dfrac { 3 } { { { { \ sin } ^ 2 } x } } + 3 { \ tan ^ 2 } x + \ tan x + \ cot x = m \ \ \ Leftrightarrow 3 \ left ( { 1 + { { \ cot } ^ 2 } x } \ right ) + 3 { \ tan ^ 2 } x + \ tan x + \ cot x = m \ \ \ Leftrightarrow 3 \ left ( { { { \ tan } ^ 2 } x + { { \ cot } ^ 2 } x } \ right ) + \ tan x + \ cot x + 3 = m \ end { array } \ )
Đặt \ ( t = \ tan x + \ cot x \, \, \ left ( { \ left | t \ right | \ ge 2 } \ right ) \ Rightarrow { \ tan ^ 2 } x + { \ cot ^ 2 } x = { t ^ 2 } – 2 \ ) .
Phương trình trở thành : \ ( 3 \ left ( { { t ^ 2 } – 2 } \ right ) + t + 3 = m \ Leftrightarrow 3 { t ^ 2 } + t – 3 = m \ ) .
Yêu cầu bài toán : Tìm \ ( m \ ) để phương trình \ ( 3 { t ^ 2 } + t – 3 = m \ ) ( * ) có nghiệm thỏa mãn nhu cầu \ ( \ left | t \ right | \ ge 2 \ ) .
Xét hàm số \ ( f \ left ( t \ right ) = 3 { t ^ 2 } + t – 3 \ ) ta có BBT :

Phương trình ( * ) có nghiệm \ ( \ Leftrightarrow m \ ge 7 \ ) .
Kết hợp điều kiện kèm theo \ ( m \ ) nguyên, \ ( m < 2018 \ Rightarrow \ ) Có \ ( 2011 \ ) giá trị của \ ( m \ ) thỏa mãn nhu cầu nhu yếu bài toán .

Chọn D

Đáp án – Lời giải

Source: http://wp.ftn61.com
Category: Hỏi Đáp