Tóm tắt nội dung bài viết
- Các dạng phương trình lượng giác
- Phương trình sinx = m
- Phương trình cosx = m
- Phương trình tanx = m
- Phương trình cot(x) = m
- Phương trình lượng giác chứa tham số
- Phương pháp 1: Đưa về dạng phương trình lượng giác cơ bản
- Phương pháp 2: Sử dụng phương pháp khảo sát
- cotx=m
- Một số dạng toán
- Biến đổi
- Tìm nghiệm và số nghiệm
- Tìm giâ trị lớn nhất và nhỏ nhất
- Tìm nghiệm âm lớn nhất và nghiệm dương nhỏ nhất
- Tìm tập giá trị
- Video liên quan
Các dạng phương trình lượng giác
Phương trình sinx = m
Nếu \ ( \ left | m \ right | \ ) > 1 : Phương trình vô nghiệm
Nếu \(\left | m \right |\) \(\leq\) 1 thì chọn 1 góc \(\alpha\) sao cho \(\sin \alpha = m\).
Bạn đang đọc: Tìm tất cả các giá trị thực của tham số m để phương trình cos x + sin x = căn 2 m bình + 1 vô nghiệm
Khi đó nghiệm của phương trình là \ ( \ left \ { \ begin { matrix } x = \ alpha + k2 \ pi và \ \ x = \ pi – \ alpha + k2 \ pi và \ end { matrix } \ right. \ ) với \ ( k \ epsilon \ mathbb { Z } \ )
Phương trình cosx = m
Nếu \ ( \ left | m \ right | \ ) > 1 : Phương trình vô nghiệm
Nếu \ ( \ left | m \ right | \ ) \ ( \ leq \ ) 1 thì chọn 1 góc \ ( \ alpha \ ) sao cho \ ( \ cos \ alpha = m \ ) .
Khi đó nghiệm của phương trình là \ ( \ left \ { \ begin { matrix } x = \ alpha + k2 \ pi và \ \ x = – \ alpha + k2 \ pi và \ end { matrix } \ right. \ ) với \ ( k \ epsilon \ mathbb { Z } \ )
Phương trình tanx = m
Chọn góc \ ( \ alpha \ ) sao cho \ ( \ tan \ alpha = m \ ) .
Khi đó phương trình luôn có nghiệm với mọi m .
\ ( \ tan x = \ tan \ alpha \ Leftrightarrow x = \ alpha + k \ pi ( k \ epsilon \ mathbb { Z } ) \ )
Hoặc \ ( \ tan x = m \ Leftrightarrow m – \ arctan m + k \ pi \ ) ( m bất kể )
Chú ý : \ ( \ tan x = 0 \ Leftrightarrow x = k \ pi \ ), \ ( \ tan x \ ) không xác lập khi \ ( x = \ frac { \ pi } { 2 } + k \ pi \ )
Phương trình cot(x) = m
Chọn góc \ ( \ alpha \ ) sao cho \ ( \ csc \ alpha = m \ ) .
Khi đó phương trình luôn có nghiệm với mọi m .
\ ( \ csc x = \ csc \ alpha \ Leftrightarrow x = \ alpha + k \ pi ( k \ epsilon \ mathbb { Z } ) \ ) Hoặc \ ( \ cot x = m \ Leftrightarrow m = \ textrm { arccsc } m + k \ pi \ ) ( m bất kể )
Chú ý : \ ( \ csc x = 0 \ Leftrightarrow x = \ frac { \ pi } { 2 } + k \ pi \ ) ,
\ ( \ csc x \ ) không xác lập khi \ ( x = k \ pi \ )
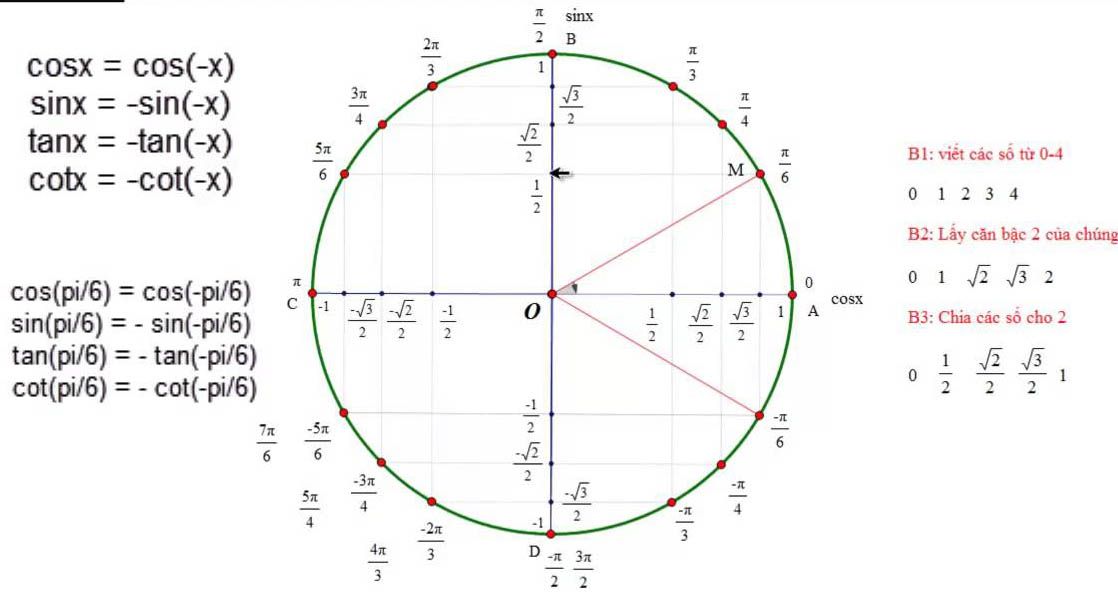
Vòng tròn lượng giác cho những bạn tìm hiểu thêm :
Phương trình lượng giác chứa tham số
Phương trình lượng giác chứa tham số dạng \ ( a \ sin x + b \ cos x = c \ ) có nghiệm khi và chỉ khi \ ( a ^ { 2 } + b ^ { 2 } \ geq c ^ { 2 } \ )
Để giải phương trình lượng giác chứa tham số có hai cách làm phổ cập là :
- Thứ nhất đưa về PT lượng giác cơ bản
- Thứ hai sử dụng chiêu thức khảo sát hàm
Phương pháp 1: Đưa về dạng phương trình lượng giác cơ bản
- Điều kiện có nghiệm của phương trình lượng giác
- Kết hợp những kiến thức và kỹ năng đã học đưa ra những điều kiện kèm theo làm cho phương trình dạng cơ bản có nghiệm thỏa điều kiện kèm theo cho trước
Ví dụ: Xác định m để phương trình \((m^{2} – 3m + 2)\cos ^{2}x = m(m-1)\) (1) có nghiệm.
Cách giải
\ ( ( 1 ) \ Leftrightarrow ( m-1 ) ( m-2 ) \ cos ^ { 2 } x = m ( m-1 ) \ ) ( 1 ’ )
Khi m = 1 : ( 1 ) luôn đúng với mọi \ ( x \ epsilon \ mathbb { R } \ )
Khi m = 2 : ( 1 ) vô nghiệm
Khi \ ( m \ neq 1 ; m \ neq 2 \ ) thì :
( 1 ’ ) \ ( \ Leftrightarrow ( m-2 ) \ cos ^ { 2 } x = m \ Leftrightarrow \ cos ^ { 2 } x = \ frac { m } { m-2 } \ ) ( 2 )
Khi đó ( 2 ) có nghiệm \ ( \ Leftrightarrow 0 \ leq \ frac { m } { m-2 } \ leq 1 \ Leftrightarrow m \ leq 0 \ )
Vậy ( 1 ) có nghiệm khi và chỉ khi m = 1, \ ( m \ leq 0 \ )
Phương pháp 2: Sử dụng phương pháp khảo sát
Giả sử phương trình lượng giác chứa tham số m có dạng : g ( x, m ) = 0 ( 1 ). Xác định m để phương trình ( 1 ) có nghiệm \ ( x \ epsilon D \ )
Phương pháp:
- Đặt ẩn phụ t = h ( x ) trong đó h ( x ) là 1 biểu thức thích hợp trong phương trình ( 1 )
-
Tìm miền giá trị (điều kiện) của t trên tập xác định D. Gọi miền giá trị của t là D1
- Đưa phương trình ( 1 ) về phương trình f ( m, t ) = 0
- Tính f ’ ( m, t ) và lập bảng biến thiên trên miền D1
- Căn cứ vào bảng biến thiên và hiệu quả của bước 4 mà những định giá trị của m .
Trên đây là bài tổng hợp kỹ năng và kiến thức về phương trình lượng giác của DINHNGHIA.VN. Nếu có góp ý hay do dự vướng mắc gì những bạn phản hồi bên dưới nha. Cảm ơn những bạn ! Nếu thấy hay thì san sẻ nhé ^ ^
Xem chi tiết cụ thể qua bài giảng dưới đây nhé :
(Nguồn: www.youtube.com)
Please follow and like us :

trong : Toán học, Toán học lớp 11, Đại số Xem mã nguồn
- m
[-1;1] => phương trình vô nghiệm
- m ∈ [-1;1] thì:
- sinx=sinα (α = SHIFT sin)
x = α + k2.π hoặc x = pi – α + k2.π (α: rad, k∈Z)
x = a + k.360° hoặc x = 180° – a + k.360° (a: độ°, k∈Z)
- Nếu m không là “giá trị đặc biệt” thì:
- x = arcsinm + k2.pi (arc = SHIFT sin)
- x = pi – arcsinm + k2.pi
- sinx = 1 <=> x=
- sinx = -1 <=> x=
- sinx = 0 <=> x=k.pi
- m [-1;1] => phương trình vô nghiệm
- m ∈ [-1;1] thì:
- cosx=cosα (α = SHIFT sin)
x = ±α + k2.pi (α: rad, k∈Z)
x = ±a + k.360° (a: độ°, k∈Z)
- Nếu m không là “giá trị đặc biệt” thì:
- x = ±arccosm + k2.pi (arc = SHIFT cos)
- cosx = 1 <=> x=
- cosx = -1 <=> x=
- cosx = 0 <=> x=
- tanx=tanα (α = SHIFT tan)
<=> x = α + k.pi (α: rad, k∈Z)
<=> x = a + k.360° (α: độ°, k∈Z)
- Nếu m “không là giá trị đặc biệt thì
cotx=m
- cotx=cotα (α = SHIFT tan(1/m))
<=> x = α + k.pi (α: rad, k∈Z)
<=> x = a + k.360° (α: độ°, k∈Z)
- Nếu m “không là giá trị đặc biệt thì
Xem lại các giá trị lượng giác của các góc, cung đặc biệt:
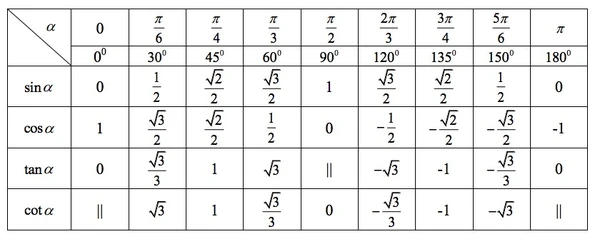
Một số dạng toán
Biến đổi
- sinf(x) = -sing(x) = sin(-g(x))
- sinf(x) = cosg(x) → sinf(x) = sin(pi/2 – g(x))
- sinf(x) = -cosg(x) → cosg(x) = -sinf(x) = sin(-f(x)) → cosg(x) = cos(pi/2 – f(x))
- Khi có
, ta thường “hạ bậc tăng cung”.
Tìm nghiệm và số nghiệm
1 ) Giải phương trình A với x ∈ a .
- Trước hết tìm họ nghiệm của phương trình a.
- Xét x trong a. Lưu ý k ∈ Z. Khi tìm được k, quay lại họ nghiệm để tìm ra nghiệm x.
2 ) Tìm số nghiệm k
- Các bước tương tự như trên.
- Tìm được k → số nghiệm.
Tìm giâ trị lớn nhất và nhỏ nhất


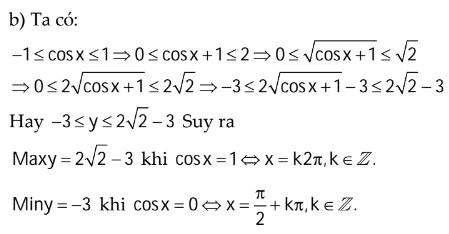
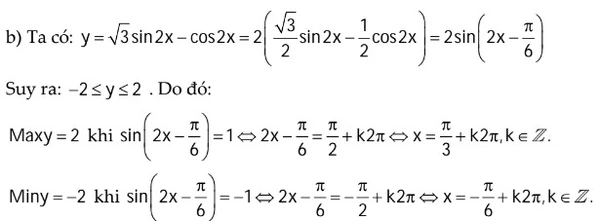


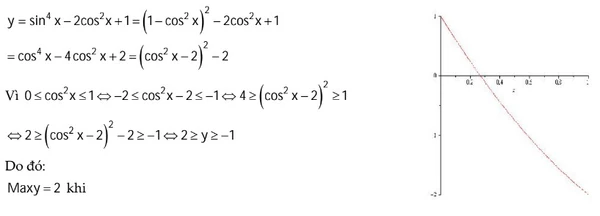

Tìm nghiệm âm lớn nhất và nghiệm dương nhỏ nhất
1 ) Với nghiệm âm lớn nhất
- Xét x < 0 (k ∈ Z)
- Thay vào họ nghiệm để tìm nghiệm.
2 ) Với nghiệm dương nhỏ nhất
- Xét x > 0 (k ∈ Z)
- Thay vào họ nghiệm để tìm nghiệm.
Tìm tập giá trị
Tìm tập giá trị của phương trình A .
- Biến đổi phương trình về dạng phương trình bậc hai.
- Đặt phương trình lượng giác (sin, cos…) = t (nếu có điều kiện)
- Tìm đỉnh I (-b/2a; -Δ/4a)
- Vẽ bảng xét giả trị (hình minh họa): (pt âm → mũi trên đi ↑ rồi ↓ và ngược lại)
- Tìm miền giá trị tại hai điểm thuộc t (thay 2 giá trị đó vào t) rồi rút ra kết luận.
- Chú ý: Asinx + Bcosx = C
Điều kiện 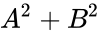

Video liên quan
Source: http://wp.ftn61.com
Category: Hỏi Đáp

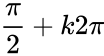
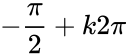

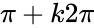




Để lại một bình luận