Tìm Tập Nghiệm Của Bất Phương Trình Lớp 10, Tìm Tập Nghiệm S Của Bất Phương Trình: 2^{{X^2}

Giải bất phương trình Toán 10

Tập nghiệm của bất phương trình môn Toán lớp 10 tổng hợp các dạng bài tập và hướng dẫn chi tiết về bất phương trình phổ biến trong các kì thi, bài kiểm tra trong chương trình trọng tâm Toán 10 nhằm giúp các bạn nắm vững kiến thức cơ bản, nâng cao kĩ năng tư duy bài tập. Chúc các bạn ôn tập hiệu quả!

Để tiện trao đổi, chia sẻ kinh nghiệm về giảng dạy và học tập các môn học lớp 10, lingocard.vn mời các thầy cô giáo, các bậc phụ huynh và các bạn học sinh truy cập nhóm riêng dành cho lớp sau: Nhóm Tài liệu học tập lớp 10. Rất mong nhận được sự ủng hộ của các thầy cô và các bạn.

Đang xem: Tìm tập nghiệm của bất phương trình

Tài liệu do lingocard.vn biên soạn và đăng tải, nghiêm cấm các hành vi sao chép với mục đích thương mại.

Tìm tập nghiệm của bất phương trình 

1. Tập nghiệm S của bất phương trình là gì?

Trước hết ta xét đến định nghĩa bất phương trình một ẩn
– Bất phương trình một ẩn là một mệnh đề chứa biến x so sánh hai hàm số f ( x ) và g ( x ) trên trường số thực dưới một trong những dạng
f ( x ) g ( x ) ; f ( x ) ≥ g ( x ) ; f ( x ) ≤ g ( x )
– Giao của hai tập xác lập của những hàm số f ( x ) và g ( x ) được gọi là tập xác lập của bất phương trình .
– Nếu với giá trị x = a, f ( a ) > 0 là bất đẳng thức đúng thì ta nói rằng a nghiệm đúng bất phương trình f ( x ) > 0, hay a là nghiệm của bất phương trình .
Xem thêm : Khóa Học hướng dẫn Khóa Học Online
Tập hợp tổng thể những nghiệm của bất phương trình được gọi là tập nghiệm của bất phương trình

2. Bài tập ví dụ minh họa

Bài tập 1: Tìm tập nghiệm S của bất phương trình

Hướng dẫn giải

Điều kiện xác lập :
Bất phương trình tương tự :
( * * )

Kết hợp với điều kiện kèm theo ( * * )

Vậy tập nghiệm của bất phương trình là

Bài tập 2: Tìm tập nghiệm của bất phương trình:

Hướng dẫn giải

Điều kiện xác lập x2 – 6 x + 8 ≠ 0 ⟺ x ≠ 2, x ≠ 4

Lập bảng xét dấu ta có :
Từ bảng xét dấu ta Kết luận : Tập nghiệm của bất phương trình là : x ∈ < - 2 ; 4 )

Bài tập 3: Giải bất phương trình: (x2 + 3x + 1)(x2 + 3x – 3) ≥ 5 (*)

Hướng dẫn giải

Tập xác lập D =

Đặt x2 + 3 x – 3 = t ⟹ x2 + 3 x + 1 = t + 4
Bất phương trình ( * ) ⟺ t ( t + 4 ) ≥ 5

⟺ t2 + 4 t – 5 ≥ 0
⟺ t ∈ ( – ∞ ; – 5 > ∪ < 1 ; + ∞ ) Vậy tập nghiệm của bất phương trình là x ∈ ( - ∞ ; - 4 > ∪ < 1 ; + ∞ )

3. Bài tập tự rèn luyện

Câu 1: Tìm tập nghiệm S của bất phương trình x2- 4 > 0

A. S = (-2 ; 2).	B. S = (-∞ ; -2) ∪ (2; +∞)
C. S = (-∞ ; -2> ∪ <2; +∞)	D. S = (-∞ ; 0) ∪ (4; +∞)

Câu 2: Tìm tập nghiệm S của bất phương trình x2 – 4x + 4 > 0.

Xem thêm : Khóa Học Ielts Speaking Online Miễn Phí, Khóa Học Ielts Trực Tuyến

A. S = R	B. S = R{2}
C. S = (2; ∞)	D. S =R{-2}

Câu 3: Tập nghiệm S = (-4; 5) là tập nghiệm của bất phương trình nào sau đây?

A. (x + 4)(x + 5)	B. (x + 4)(5x – 25) ≥ 0
C. (x + 4)(x + 25)	D. (x – 4)(x – 5)

Câu 4: Cho biểu thức: f(x) = ax2 + bx + c (a ≠0) và ∆ = b2 – 4ac. Chọn khẳng định đúng trong các khẳng định dưới đây?

A. Khi ∆ 0 thì f ( x ) trái dấu với thông số a với mọi x ∈
.

Câu 5: Tìm tập nghiệm của bất phương trình: -x2 + 2017x + 2018 > 0

A. S =	B. S = (-∞ ; -1) ∪ (2018; +∞)
C. S = (-∞ ; -1> ∪ <2018; +∞)	D. S = (-1 ; 2018)

Câu 6: Giải các bất phương trình sau:

a.	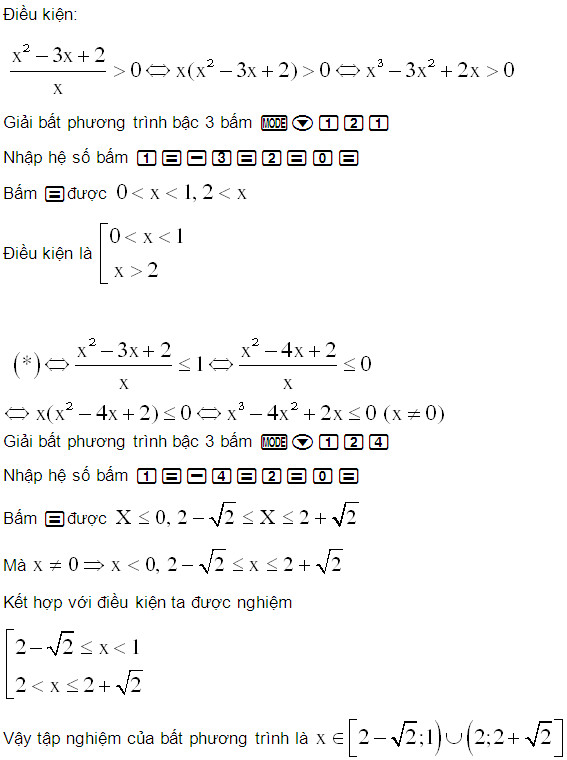b.
c.	d.

Câu 7: Tìm tập nghiệm của các bất phương trình sau:

a.
c.	d.
e.	f.

——————————————————–

Trên đây là Cách tìm tập nghiệm S của bất phương trình lingocard.vn giới thiệu tới quý thầy cô và bạn đọc. Hy vọng với tài liệu này các bạn học sinh sẽ nắm chắc kiến thức vận dụng tốt vào giải bài tập từ đó học tốt môn Toán lớp 10. Chúc các bạn học tốt và nhớ thường xuyên tương tác để cập nhật được nhiều bài tập hay bổ ích nhé!

Xem thêm bài viết thuộc chuyên mục: Phương trình

Điều hướng bài viết

Source: http://wp.ftn61.com
Category: Hỏi Đáp