Chứng minh phương trình luôn có nghiệm với mọi m

3
/
5
(
2
bầu chọn
)

Để Chứng minh phương trình luôn có nghiệm với mọi m trước tiên cùng tìm hiểu phương trình bậc 2 và những kiến thức liên quan trong chương trình toán học trung học cơ sở. Các bạn học sinh và quý thầy cô và phụ huynh cùng tham khảo nhé. 

1. Phương trình bậc 2 là gì?

Phương trình bậc 2 là phương trình có dạng :
ax2 + bx + c = 0 ( a ≠ 0 ), được gọi là phương trình bậc 2 với ẩn là x. ( 1 )
Nhiệm vụ là phải giải phương trình trên để đi tìm giá trị của x sao cho khi thay x vào phương trình ( 1 ) thì thỏa mãn nhu cầu ax2 + bx + c = 0 .

2. Cách giải phương trình bậc 2

Cách giải phương trình bậc 2 như sau :
Bước 1 : Tính Δ = b2-4ac
Bước 2 : So sánh Δ với 0
Khi :

• Δ < 0 => phương trình ( 1 ) vô nghiệm
• Δ = 0 => phương trình ( 1 ) có nghiệm kép x = – b / 2 a
• Δ > 0 => phương trình ( 1 ) có 2 nghiệm phân biệt .

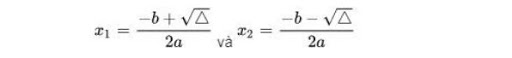
3. Định lý Viet và ứng dụng trong phương trình bậc 2 

Cho phương trình bậc 2 : ax2 + bx + c = 0 ( a ≠ 0 ). Giả sử phương trình có 2 nghiệm x1 và x2, lúc này hệ thức sau được thỏa mãn nhu cầu :

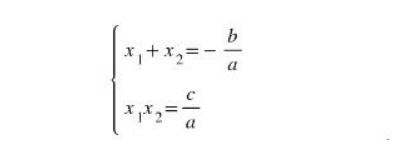
Dựa vào hệ thức trên ta hoàn toàn có thể tính biểu thức đối xứng x1, x2 trải qua định lý Viet .

• x1 + x2 = – b / a
• x12 + x22 = ( x1 + x2 ) 2-2 x1x2 = ( b2-2ac ) / a2

Định lý Viet hòn đảo giả sử như sống sót 2 số thực x1, x2 thỏa mãn nhu cầu x1 + x2 = S, x1x2 = P thì x1, x2 là 2 nghiệm của phương trình x2-Sx+P = 0

4. Một số ứng dụng thường gặp của định lý Viet trong giải phương trình bậc 2

4.1. Mẹo nhẩm nghiệm phương trình bậc 2 nhanh

Ta có cách tính nhanh nghiệm của phương trình bậc 2 ax2 + bx + c = 0 ( a ≠ 0 ) như sau :

• Nếu a + b + c = 0 thì nghiệm x1 = 1, x2 = c / a
• Nếu a-b+c = 0 thì nghiệm x1 = – 1, x2 = – c / a

4.2. Phân tích đa thức thành nhân tử

Cho đa thức P ( x ) = ax2 + bx + c

• Nếu x1 và x2 là nghiệm của phương trình P ( x ) = 0
• Thì đa thức P ( x ) = a ( x-x1 ) ( x-x2 )

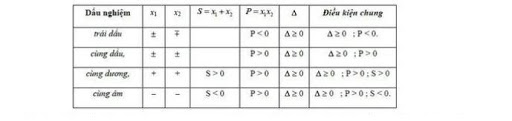
4.3. Xác định dấu của các nghiệm

Cho phương trình ax2 + bx + c = 0 ( a ≠ 0 ) ,
Giả sử x1, x2 là 2 nghiệm của phương trình trên. Theo định lý Viet, ta có :

• Nếu S < 0, x1 trái dấu x2 .
• Nếu S > 0, x1 cùng dấu x2
• P > 0, cả hai nghiệm cùng dương .
• P < 0, cả hai nghiệm cùng âm .

5. Dạng bài tập về phương trình bậc 2 

5.1. Dạng bài tập phương trình bậc 2 một ẩn không xuất hiện tham số

Để giải bài tập dạng này cách phổ cập nhất là dùng công thức Δ hoặc Δ ’ sau đó vận dụng điều kiện kèm theo và công thức như đã nêu ở mục 2. để giải .
Ví dụ : Giải những phương trình x2-3x+2 = 0 ( * )

• ta có : Δ = ( – 3 ) 2-4. 2 = 1
• suy ra nghiệm của phương trình là :

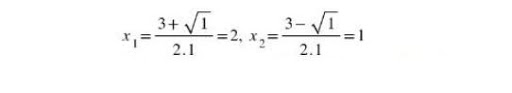
5.2. Phương trình khuyết hạng tử.

5.2.1. Khuyết hạng tử bậc nhất ax2+c=0 (1)

Xem thêm: Top 5 phần mềm kiểm tra đạo văn tốt nhất 2022

Cách giải :

• Nếu – c / a > 0, nghiệm là :

• Nếu – c / a = 0, có nghiệm x = 0
• Nếu – c / a < 0, phương trình vô nghiệm .

5.2.2. Khuyết hạng tử tự do ax2 + bx = 0 ( 2 )

Ví dụ 2 : Giải phương trình x2-4 = 0
ta có :
x2-4 = 0 ⇔ x2 = 4 ⇔ x = 2 hoặc x = – 2

5.3. Phương trình trùng phương: ax4+bx2+c=0 (a≠0)

Cách giải :

• Đặt t = x2 ( t ≥ 0 ) .
• Phương trình đã cho có dạng : at2 + bt + c = 0
• Giải như phương trình bậc 2 thông thường, điều kiện kèm theo t ≥ 0

5.3.Dạng Phương trình bậc 2 có tham số

Phương pháp giải biện luận số nghiệm của phương trình ta sử dụng công thức tính Δ, dựa vào dấu của Δ để biện luận nghiệm của phương trình .
Ví dụ : Giải và biện luận phương trình mx2-5x-m-5 = 0 ( 1 )
Cách giải :

• Xét m = 0, lúc này ( 1 ) ⇔ – 5 x – 5 = 0 ⇔ x = – 1
• Xét m ≠ 0, lúc này ( 1 ) là phương trình bậc 2 theo ẩn x .

• Δ = ( – 5 ) ^ 2 – 4 m ( – m-5 ) = ( 2 m + 5 ) ^ 2
• Vì Δ ≥ 0 nên phương trình luôn có nghiệm :
• Δ = 0 ⇔ m = – 5/2, phương trình có 1 nghiệm duy nhất .
• Δ > 0 ⇔ m ≠ – 5/2, phương trình có 2 nghiệm phân biệt :

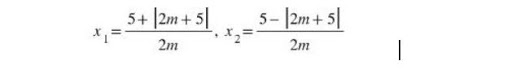
Xác định điều kiện kèm theo tham số để nghiệm thỏa nhu yếu đề bài thứ nhất phương trình bậc 2 cần có nghiệm. Các bước giải như sau :

• Tính Δ, sau đó tìm điều kiện kèm theo để Δ không âm .
• Dựa vào định lý Viet, ta có được cách tính những hệ thức giữa tích và tổng, từ đó biện luận nghiệm theo nhu yếu của đề bài .

Ví dụ : Cho pt x ^ 2 – ( m-2 ) x + m-4 = 0 ( x ẩn ; m tham số )

1. a) chứng minh phương trình luôn có nghiệm với mọi m.

Xét Δ = ( m – 2 ) ^ 2 – 4 * ( m – 4 ) = m ^ 2 – 4 m + 4 – 4 m + 16 = m ^ 2 – 8 m + 20 = ( m – 4 ) ^ 2 + 4 > = 4
Δ > = 4 > 0 với mọi m => pt luôn có hai nghiệm phân biệt với mọi m .

1. b ) Tìm giá trị của m để phương trình có 2 ng đối nhau

• phương trình có hai nghiệm đối nhau khi < => x1 + x2 = 0 < => m – 2 = 0 => m = 2
• Vậy với m = 2 phương trình có 2 nghiệm đối nhau

Ví dụ : Cho phương trình x ^ 2-2 mx + 4 m – 4 = 0 .

1. a) chứng minh phương trình luôn có nghiệm với mọi m.

2. b ) Goi x1và x2 là hai nghiệm của phương trình. tìm m để 3×1 x2 + 5 = x1 ^ 2 – x2 ^ 2

Cách giải

1. a ) Ta có :

• Δ ’ = m ^ 2 – ( 4 m – 4 ) = m ^ 2-4 m + 4 = ( m-2 ) ^ 2 ≥ 0
• ⇔ phương trình luôn có nghiệm với mọi m thuộc R

1. b ) Theo định lý Viet

x1 + x2 = 2 m ( * )
x1x2 = 4 m – 4 ( * )

⇔ 3x1x2 + 5= -x1^2 – x2^2 ⇔ 3x1x2 + 5 = -(x1+x2)^2 + 2x1x2

⇔ ( x1 + x2 ) ^ 2 + x1x2 + 5 = 0 ( * * )
ta thay phương trình ( * ) và phương trình ( * * ) sẽ ra phương trình bậc 2 ẩn m và giải như thông thường .

Kết luận

Trên đây là tổng hợp những kiến thức cơ bản của phương trình bậc 2 và phương pháp chứng minh phương trình luôn có nghiệm với mọi m. Mong rằng những thông tin trên sẽ giúp ích cho các bạn học sinh và quý thầy cô tham khảo trong học tập và giảng dạy. 

Source: http://wp.ftn61.com
Category: Hỏi Đáp