Phương trình lượng giác cơ bản và các dạng bài tập có lời giải từ A – Z

Trong bài viết này, chúng tôi sẽ san sẻ triết lý và những dạng bài tập về phương trình lượng giác cơ bản giúp những ôn lại kỹ năng và kiến thức để sẵn sàng chuẩn bị hành trang thật kỹ cho những kỳ thi đạt kết qua cao nhé

Lý thuyết phương trình lượng giác cơ bản thường gặp

1. Phương trình sin x = sin α, sin x = a (1)

Nếu | a | > 1 thì phương trình vô nghiệm .
Nếu | a | ≤ 1 thì chọn cung α sao cho sinα = a. Khi đó ( 1 )

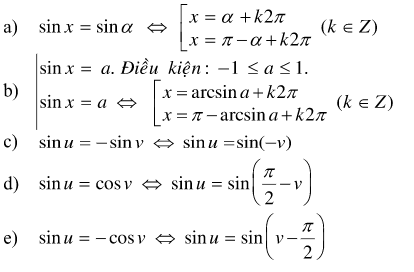
Các trường hợp đặc biệt:

sin x = 0 ⇔ x = kπ ( k ∈ Z )
sin x = 1 ⇔ x = π / 2 + k2π ( k ∈ Z )
sin x = – 1 ⇔ x = – π / 2 + k2π ( k ∈ Z )
sin x = ± 1 ⇔ sin2x = 1 ⇔ cos2x = 0 ⇔ cosx = 0 ⇔ x = π / 2 + kπ ( k ∈ Z )

2. Phương trình cos x = cos α, cos x = a (2)

Nếu | a | > 1 thì phương trình vô nghiệm .
Nếu | a | ≤ 1 thì chọn cung α sao cho cosα = a .
Khi đó ( 2 ) ⇔ cosx = cosα ⇔ x = ± α + k2π ( k ∈ Z )
b. cosx = a điều kiện kèm theo – 1 ≤ a ≤ 1
cosx = a ⇔ x = ± arccosa + k2π ( k ∈ Z )
c. cosu = cosv ⇔ cosu = cos ( π – v )
d. cosu = sinv ⇔ cosu = cos ( π / 2 – v )
e. cosu = – sinv ⇔ cosu = cos ( π / 2 + v )

Các trường hợp đặc biệt:

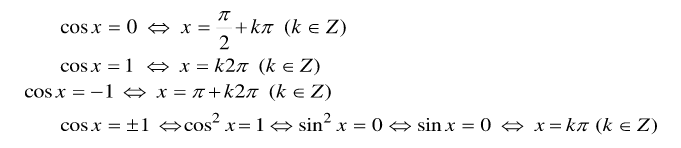
3. Phương trình tan x = tan α, tan x = a (3)

Chọn cung α sao cho tanα = a. Khi đó ( 3 )

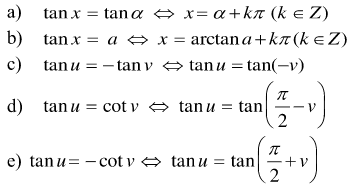
Các trường hợp đặc biệt:

tanx = 0 ⇔ x = kπ ( k ∈ Z )
tanx = ± 1 ⇔ x = ± π / 4 + kπ ( k ∈ Z )

4. Phương trình cot x = cot α, cot x = a (4)

Chọn cung α sao cho cotα = a .
Khi đó ( 3 ) cotx = cotα ⇔ x = α + kπ ( k ∈ Z )
cotx = a ⇔ x = arccota + kπ ( k ∈ Z )

Các trường hợp đặc biệt:

cotx = 0 ⇔ x = π / 2 + kπ ( k ∈ Z )
cotx = ± 1 ⇔ x = ± π / 4 + kπ ( k ∈ Z )

5. Phương trình bậc nhất đối với một hàm số lượng giác

Dạng asinx + b ; acosx + b = 0 ; atanx + b = 0 ; acotx + b = 0 ( a, b ∈ Ζ, a ≠ 0 )
Cách giải :
Đưa về phương trình cơ bản, ví dụ asinx + b = 0 ⇔ sinx = – b / a

Tham khảo thêm:

6. Phương trình bậc hai đối với một hàm số lượng giác

Dạng asin2x + bsinx + c = 0 ( a, b ∈ Ζ, a ≠ 0 )
Phương pháp
Đặt ẩn phụ t, rồi giải phương trình bậc hai so với t .
Ví dụ : Giải phương trình asin2x + bsinx + c = 0
Đặt t = sinx ( – 1 ≤ t ≤ 1 ) ta có phương trình at2 + bt + c = 0
Lưu ý khi đặt t = sinx hoặc t = cosx thì phải có điều kiện kèm theo – 1 ≤ t ≤ 1

7. Một số điều cần chú ý:

a ) Khi giải phương trình có chứa những hàm số tang, cotang, có mẫu số hoặc chứa căn bậc chẵn, thì nhất thiết phải đặt điều kiện kèm theo để phương trình xác lập

b ) Khi tìm được nghiệm phải kiểm tra điều kiện kèm theo. Ta thường dùng một trong những cách sau để kiểm tra điều kiện kèm theo :

• Kiểm tra trực tiếp bằng cách thay giá trị của x vào biểu thức điều kiện.
• Dùng đường tròn lượng giác để biểu diễn nghiệm
• Giải các phương trình vô định.

c ) Sử dụng MTCT để thử lại những đáp án trắc nghiệm

Các dạng bài tập về phương trình lượng giác

Dạng 1: Giải phương trình lượng giác cơ bản

Phương pháp: Dùng các công thức nghiệm tương ứng với mỗi phương trình

Ví dụ 1 : Giải những phương trình lượng giác sau :
a ) sinx = sin ( π / 6 ). c ) tanx – 1 = 0
b ) 2 cosx = 1. d ) cotx = tan2x .
Lời giải
a ) sin ⁡ x = sin ⁡ π / 6

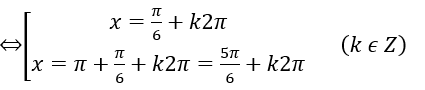
b ) 2 cosx = 1 ⇔ cosx = ½ ⇔ x = ± π / 3 + k2π ( k ∈ Z )
c ) tan ⁡ x = 1 ⇔ cos ⁡ x = π / 4 + kπ ( k ∈ Z )
d ) cot ⁡ x = tan ⁡ 2 x
⇔ cotx = cot ( π / 2 – 2 x )
⇔ x = π / 2 – 2 x + kπ
⇔ x = π / 6 + kπ / 3 ( k ∈ Z )
Ví dụ 2 : Giải những phương trình lượng giác sau :
a ) cos2 x – sin2x = 0 .

b) 2sin(2x – 40º) = √3

Lời giải
a ) cos2x – sin2x = 0 ⇔ cos2x – 2 sin ⁡ x.cos ⁡ x = 0
⇔ cos ⁡ x ( cos ⁡ x – 2 sin ⁡ x ) = 0

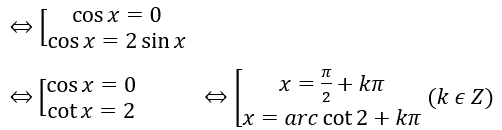
b ) 2 sin ⁡ ( 2 x – 40 º ) = √ 3
⇔ sin ⁡ ( 2 x – 40 º ) = √ 3/2

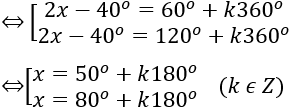
Ví dụ 3 : Giải những phương trình sau : ( √ 3-1 ) sinx = 2 sin2x .

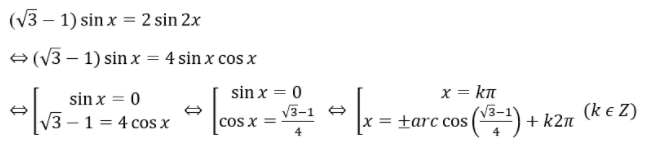
Dạng 2: Phương trình bậc nhất có một hàm lượng giác

Phương pháp : Đưa về phương trình cơ bản, ví dụ asinx + b = 0 ⇔ sinx = – b / a
Ví dụ : Giải phương trình sau :

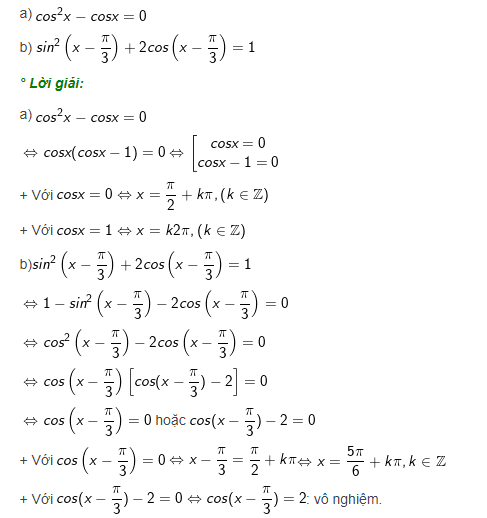
Dạng 3: Phương trình bậc hai có một hàm lượng giác 

Phương pháp

Phương trình bậc hai so với một hàm số lượng giác là phương trình có dạng :
a. f2 ( x ) + b. f ( x ) + c = 0 với f ( x ) = sinu ( x ) hoặc f ( x ) = cosu ( x ), tanu ( x ), cotu ( x ) .
Cách giải :
Đặt t = f ( x ) ta có phương trình : at2 + bt + c = 0
Giải phương trình này ta tìm được t, từ đó tìm được x
Khi đặt t = sinu ( x ) hoặc t = cosu ( x ), ta có điều kiện kèm theo : – 1 ≤ t ≤ 1
Ví dụ : sin2x + 2 sinx – 3 = 0

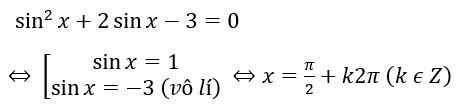
Ví dụ 2 : 1 + sin2x + cosx + sinx = 0
Lời giải :
⇔ 1 + 2 sin ⁡ x cos ⁡ x + 2 ( cos ⁡ x + sin ⁡ x ) = 0
⇔ cos2 ⁡ x + sin2 ⁡ x + 2 sin ⁡ xcos ⁡ x + 2 ( cos ⁡ x + sin ⁡ x ) = 0
⇔ ( sin ⁡ x + cos ⁡ x ) 2 + 2 ( cos ⁡ x + sin ⁡ x ) = 0

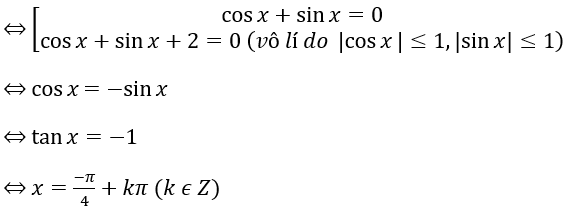
Dạng 4: Phương trình bậc nhất theo sinx và cosx

Xét phương trình asinx + bcosx = c ( 1 ) với a, b là những số thực khác 0 .

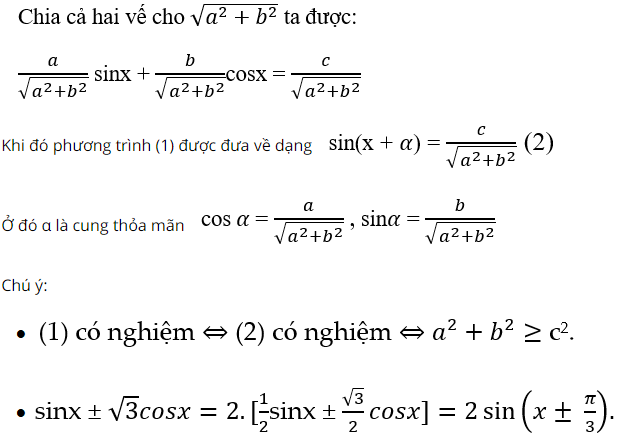
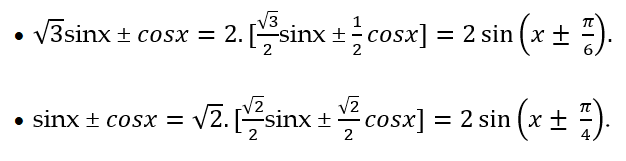
Ví dụ : Giải phương trình sau : cos2x – sin2x = 0 .

Dạng 5: Phương trình lượng giác đối xứng, phản đối xứng

Phương pháp

Phương trình đối xứng là phương trình có dạng :
a ( sinx + cosx ) + bsinxcosx + c = 0 ( 3 )
Phương pháp giải :
Để giải phương trình trên ta sử dụng phép đặt ẩn phụ :

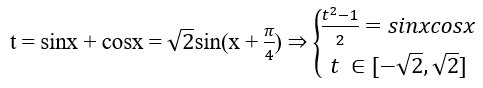
Thay vào ( 3 ) ta được phương trình bậc hai theo t .
Ngoài ra tất cả chúng ta còn gặp phương trình phản đối xứng có dạng :
a ( sinx – cosx ) + bsinxcosx + c = 0 ( 4 )
Để giải phương trình này ta cũng đặt

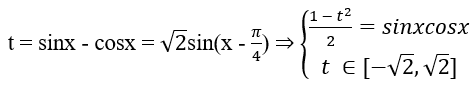
Thay vào ( 4 ) ta có được phương trình bậc hai theo t .
Ví dụ 1 : Giải phương trình sau : 2 ( sinx + cosx ) + 3 sin2x = 2 .

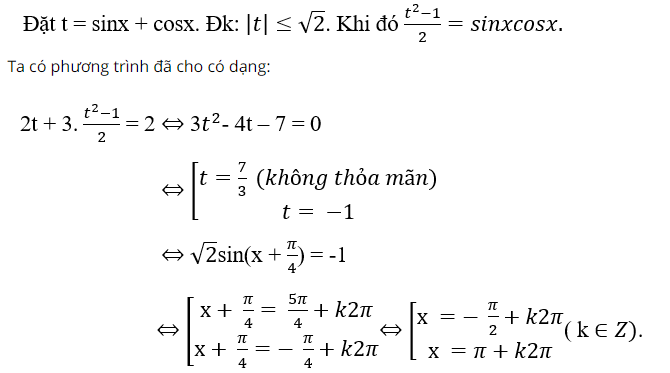
Hy vọng với những kiến thức và kỹ năng mà chúng tôi vừa san sẻ hoàn toàn có thể giúp những bạn mạng lưới hệ thống lại kiến thức và kỹ năng về phương trình lượng giác cơ bản từ đó vận dụng vào làm bài tập nhanh gọn và đúng chuẩn nhé

5/5 – ( 1 bầu chọn )

Source: http://wp.ftn61.com
Category: Hỏi Đáp