Tóm tắt nội dung bài viết
Tìm hoành độ giao điểm của đồ thị hàm số
Phương pháp giải
+ Điểm M ( x0 ; y0 ) thuộc đồ thị hàm số y = f ( x ) ⇔ y0 = f ( x0 ) .
+ Hoành độ giao điểm của đồ thị hàm số y = f ( x ) và y = g ( x ) là nghiệm của phương trình f ( x ) = g ( x ) .
Ví dụ minh họa
Ví dụ 1: Những điểm nào dưới đây thuộc đồ thị hàm số y = 2×2 + 3x + 1.
A ( 0 ; 3 ) ; B ( 0 ; 1 ) ; C ( 1 ; 0 ) ; D ( – 50% ; 0 ) E ( – 1 ; 0 ) .
Hướng dẫn giải:
Đặt f ( x ) = 2 × 2 + 3 x + 1 .
Ta có :
+ f ( 0 ) = 2.02 + 3.0 + 1 = 1 ⇒ A ( 0 ; 3 ) không thuộc đồ thị hàm số và B ( 0 ; 1 ) thuộc đồ thị hàm số .
+ f ( 1 ) = 2.12 + 3.1 + 1 = 6 ⇒ C ( 1 ; 0 ) không thuộc đồ thị hàm số .
+ f ( – 50% ) = 2. ( – 50% ) 2 + 3 ( – 50% ) + 1 = 0 ⇒ D ( – 50% ; 0 ) thuộc đồ thị hàm số .
+ f ( – 1 ) = 2. ( – 1 ) 2 + 3. ( – 1 ) + 1 = 0 ⇒ E ( – 1 ; 0 ) thuộc đồ thị hàm số .
Ví dụ 2: Tìm m để A(1; 2) thuộc các đồ thị hàm số dưới đây:
a ) y = f ( x ) = x2 + 2 x + m
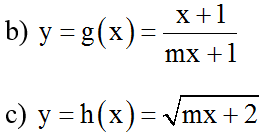
Hướng dẫn giải:
a ) A ( 1 ; 2 ) thuộc đồ thị hàm số y = f ( x ) = x2 + 2 x + m
⇔ 2 = 12 + 2.1 + m
⇔ m = – 1 .
Vậy m = – 1 .
b) A(1; 2) thuộc đồ thị hàm số
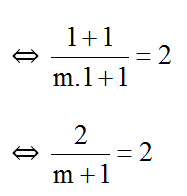
⇔ m = 0 .
Vậy m = 0 .
c) A(1; 2) thuộc đồ thị hàm số
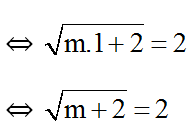
⇔ m + 2 = 4
⇔ m = 2 .
Vậy m = 2 .
Ví dụ 3: Tìm giao điểm của hai đồ thị hàm số y = 2×2 + 3x + 1 và y = x + 1.
Hướng dẫn giải:
Hoành độ giao điểm của hai hàm số là nghiệm của phương trình :
2 × 2 + 3 x + 1 = x + 1
⇔ 2 × 2 + 2 x = 0
⇔ 2 x ( x + 1 ) = 0
+ Với x = 0 thì y = x + 1 = 1 .
+ Với x = – 1 thì y = x + 1 = 0 .
Vậy hai đồ thị hàm số trên có 2 giao điểm là A ( 0 ; 1 ) và B ( – 1 ; 0 ) .
Bài tập trắc nghiệm tự luyện
Bài 1: Điểm nào dưới đây thuộc đồ thị hàm số y = 2×2 + x.
A. ( 0 ; 0 ) B. ( 0 ; 1 ). C. ( 1 ; 0 ) D. ( 2 ; 0 ) .
Bài 2: Điểm A(1; 0) không thuộc đồ thị hàm số nào dưới đây?
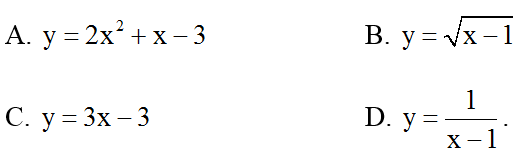
Bài 3: Với giá trị nào của a dưới đây thì đồ thị hàm số y = 3×2 + ax + 1 đi qua điểm M(-2; 0).
A. a = 13/2 B. a = 13 .
C. a = – 13 D. a = – 13/2 .
Bài 4: Hoành độ giao điểm của đồ thị hàm số y = x + 1 và y = 2x + 1 là:
A. x = 0 B. x = – 1 C. x = – 1/2 D. x = – 2 .
Bài 5: Số giao điểm của đồ thị hàm số y = √(x-1) và y = x – 1 là:
A. 0 B. 1 C. 2 D. Vô số .
Bài tập tự luận tự luyện
Bài 6: Tìm một điểm bất kì thuộc đồ thị hàm số y = 2×2 + x + 3.
Hướng dẫn giải:
y = 2 × 2 + x + 3
Chọn x = 1 ⇒ y = 2.12 + 1 + 3 = 6 .
Vậy chọn được điểm ( 1 ; 6 ) thuộc đồ thị hàm số .
Lưu ý : Các bạn hoàn toàn có thể chọn được vô số điểm khác .
Bài 7: Tìm điểm thuộc đồ thị hàm số 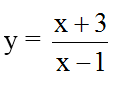
Hướng dẫn giải:
Xét 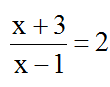
Vậy điểm có tung độ bằng 2 thuộc đồ thị hàm số là ( 5 ; 2 ) .
Bài 8: Tìm a để đồ thị hàm số y = 3×2 + 2ax + 1 đi qua điểm M(-2; 2).
Hướng dẫn giải:
Đồ thị hàm số y = 3 × 2 + 2 ax + 1 đi qua điểm M ( – 2 ; 2 )
⇔ 3. ( – 2 ) 2 + 2. a. ( – 2 ) + 1 = 2
⇔ 13 – 4 a = 2
⇔ 4 a = 11
⇔ a = 11/4 .
Vậy a = 11/4 .
Bài 9: Tìm giao điểm của đồ thị hàm số y = 3×2 + x – 2 và y = 2×2 – x + 1.
Hướng dẫn giải:
Hoành độ giao điểm của hai đồ thị hàm số là nghiệm của phương trình :
3 × 2 + x – 2 = 2 × 2 – x + 1
⇔ x2 + 2 x – 3 = 0
⇔ ( x – 1 ) ( x + 3 ) = 0
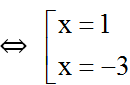
+ Với x = 1 thì y = 3.12 + 1 – 2 = 2
+ Với x = – 3 thì y = 3. ( – 3 ) 2 + ( – 3 ) – 2 = 22
Vậy hai đồ thị hàm số trên có hai giao điểm là ( 1 ; 2 ) và ( – 3 ; 22 ) .
Bài 10: Tìm a; b để đồ thị hàm số y = ax2 + x + b đi qua A(1; 2) và B(2; 0).
Hướng dẫn giải:
Đồ thị hàm số y = ax2 + x + b đi qua A ( 1 ; 2 ) và B ( 2 ; 0 )
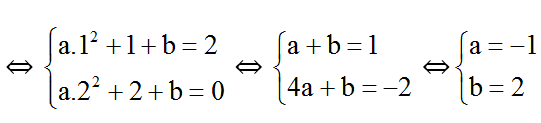
Vậy a = -1; b = 2.
Xem thêm những dạng bài tập Toán lớp 9 có đáp án và giải thuật cụ thể khác :
- Phương pháp Tìm tập xác định của hàm số
- Phương pháp Tìm tập giá trị của hàm số
- Xét tính đồng biến, nghịch biến của hàm số
- Cách xác định hàm số bậc nhất: tập xác định, đồng biến, nghịch biến
- Cách làm bài toán Đồ thị hàm số lớp 9 cực hay có giải chi tiết
- Bài toán hai đường thẳng song song, cắt nhau, trùng nhau
- Cách làm Bài toán đường thẳng đi qua điểm cố định cực hay
- Bài toán Đồ thị hàm số trị tuyệt đối cực hay
Mục lục các Chuyên đề Toán lớp 9:
- Chuyên đề Đại Số 9
- Chuyên đề: Căn bậc hai
- Chuyên đề: Hàm số bậc nhất
- Chuyên đề: Hệ hai phương trình bậc nhất hai ẩn
- Chuyên đề: Phương trình bậc hai một ẩn số
- Chuyên đề Hình Học 9
- Chuyên đề: Hệ thức lượng trong tam giác vuông
- Chuyên đề: Đường tròn
- Chuyên đề: Góc với đường tròn
- Chuyên đề: Hình Trụ – Hình Nón – Hình Cầu
Ngân hàng trắc nghiệm lớp 9 tại banmaynuocnong.com
- Hơn 20.000 câu trắc nghiệm Toán,Văn, Anh lớp 9 có đáp án
Giới thiệu kênh Youtube VietJack
Source: http://wp.ftn61.com
Category: Hỏi Đáp
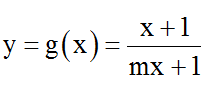
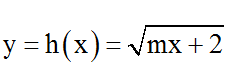
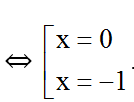



Để lại một bình luận