Tổng hợp tìm m để phương trình có nghiệm duy nhất | Bán Máy Nước Nóng - Banmaynuocnong

Tìm m để phương trình có nghiệm duy nhất
Bài viết này sẽ vấn đáp cho những em câu hỏi : Phương trình bậc 2 có nghiệm duy nhất khi nào ? điều kiện kèm theo của tham số m để phương trình bậc 2 có nghiệm duy nhất ?

I. Phương trình bậc 2 – kiến thức cơ bản cần nhớ

• Xét phương trình bậc hai: ax2 + bx + c = 0 (a≠0)

Bạn đang đọc: Tổng hợp tìm m để phương trình có nghiệm duy nhất | Bán Máy Nước Nóng – Banmaynuocnong

• Công thức nghiệm tính delta ( ký hiệu : Δ )
Δ = b2 – 4 ac

+ Nếu Δ > 0: Phương trình có 2 nghiệm phân biệt: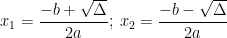

+ Nếu Δ = 0: Phương trình có nghiệm kép: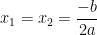

+ Nếu Δ < 0 : Phương trình vô nghiệm . • Công thức nghiệm thu sát hoạch gọn tính Δ ’ ( chỉ tính Δ ’ khi thông số b chẵn ) . Δ = b ’ 2 – ac với b = 2 b ’ .

+ Nếu Δ’ > 0: Phương trình có 2 nghiệm phân biệt: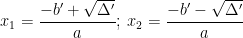

+ Nếu Δ’ = 0: Phương trình có nghiệm kép: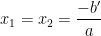

+ Nếu Δ ’ < 0 : Phương trình vô nghiệm .

→ Vậy nếu hỏi: Phương trình bậc 2 có nghiệm duy nhất khi nào?

– Trả lời: Phương trình bậc 2 có nghiệm duy nhất khi biệt thức delta = 0 (Δ = 0). (khi đó phương trình có nghiệm kép).

> Lưu ý: Nếu cho phương trình ax2 + bx + c = 0 và hỏi phương trình có nghiệm duy nhất khi nào? thì câu trả lời đúng phải là: a=0 và b≠0 hoặc a≠0 và Δ=0.

• Thực tế so với bài toán giải phương trình bậc 2 thường thì ( không chứa tham số ), thì tất cả chúng ta chỉ cần tính biệt thức delta là hoàn toàn có thể thống kê giám sát được nghiệm. Tuy nhiên bài viết này đề sẽ đề cập đến dạng toán hay làm những em hoảng sợ hơn, đó là tìm điều kiện kèm theo để phương trình bậc 2 có chứa tham số m có nghiệm duy nhất .

Xem Thêm Phường tiếng Anh là gì? Đọc ngay để có câu trả lời!

II. Một số bài tập tìm điều kiện để phương trình bậc 2 có nghiệm duy nhất.

* Phương pháp giải:

– Xác định những thông số a, b, c của phương trình, đặc biệt quan trọng là thông số a. Phương trình ax2 + bx + c = 9 là phương trình bậc 2 chỉ khi a ≠ 0 .
– Tính biệt thức delta : Δ = b2 – 4 ac
– Xét dấu của biệt thức để Tóm lại sự sống sót nghiệm, hoặc vận dụng công thức để viết nghiệm .

* Bài tập 1: Tìm các giá trị m để phương trình: mx2 – 2(m-1)x + m-3 = 0 có nghiệm duy nhất.

Xem thêm: Mã Hàng Tiếng Anh Là Gì – 700 Thuật Ngữ Tiếng Anh Xuất Nhập Khẩu

* Lời giải:

– Nếu m = 0 thì phương trình đã cho trở thành 2 x – 3 = 0 là pt bậc nhất, có nghiệm duy nhất là x = 3/2 .
– Nếu m ≠ 0, khi đó pt đã cho là pt bậc 2 một ẩn, có những thông số :
a = m ; b = – 2 ( m-1 ) ; c = m-3 .
Và Δ = [ – 2 ( m-1 ) ] 2 – 4. m. ( m-3 ) = 4 ( m2-2m+1 ) – ( 4 mét vuông – 12 m )
= 4 mét vuông – 8 m + 4-4 mét vuông + 12 m = 4 m + 4
→ Để để phương trình có nghiệm duy nhất ( nghiệm kép ) thì Δ = 0 ⇔ 4 m + 4 = 0 ⇔ m = – 1 .
⇒ Kết luận : Phương trình đã cho có nghiệm duy nhất khi và chỉ khi m = 0 hoặc m = – 1 .

* Bài tập 2: Tìm giá trị của m để phương trình sau có nghiệm duy nhất: 3×2 + 2(m-3)x + 2m+1 = 0.

* Lời giải:

– Ta tính biệt thức delta thu gọn : Δ ’ = ( m-3 ) 2 – 3 ( 2 m + 1 ) = mét vuông – 6 m + 9 – 6 m – 3 = mét vuông – 12 m + 6 .
→ Phương trình có nghiệm duy nhất ( pt bậc 2 có nghiệm kép ) khi :
Δ ’ = 0 ⇔ mét vuông – 12 m + 6 = 0 ( * )
Giải phương trình ( * ) là pt bậc 2 theo m bằng cách tính Δ ’ m = ( – 6 ) 2 – 6 = 30 > 0 .

Xem Thêm Game Bắn Súng Tiếng Anh Là Gì, Bắn Súng Trong Tiếng Anh Là Gì – Game Thủ 247

→ Phương trình (*) có 2 nghiệm phân biệt: