Bài viết này giúp bạn đọc hiểu được định nghĩa giao thoa sóng, điều kiện để xảy ra hiện tượng giao thoa và các xác định được cực đại, cực tiểu trong trường giao thoa.

2.2. Hai nguồn dao động cùng pha ( \(\Delta \varphi =\varphi _{1}-\varphi _{2}=0\)hoặc 2kπ)
Bạn đang đọc: Lý thuyết giao thoa sóng cơ
+ Độ lệch pha của hai sóng thành phần tại M: \(\Delta \varphi =\frac{2\pi }{\lambda }(d_{2}-d_{1})\)
+ Biên độ sóng tổng hợp: AM =2.A. \(\left | cos\frac{\pi }{\lambda } .(d_{2}-d_{1})\right |\)
Amax = 2. A khi : + Hai sóng thành phần tại M cùng pha => ∆ φ = 2. k. π ( \ ( k \ in Z \ ) )+ Hiệu đường đi d = d2 – d1 = k. λAmin = 0 khi : + Hai sóng thành phần tại M ngược pha nhau « ∆ φ = ( 2. k + 1 ) π ( \ ( k \ in Z \ ) )+ Hiệu đường đi d = d2 – d1 = ( k + \ ( \ frac { 1 } { 2 } \ ) ). λ+ Để xác lập điểm M xê dịch với Amax hay Amin ta xét tỉ số \ ( \ frac { d_ { 2 } – d_ { 1 } } { \ lambda } \ )- Nếu \ ( \ frac { d_ { 2 } – d_ { 1 } } { \ lambda } \ ) = k = số nguyên thì M giao động với Amax và M nằm trên cực lớn giao thoa thứ k- Nếu \ ( \ frac { d_ { 2 } – d_ { 1 } } { \ lambda } \ ) = k + \ ( \ frac { 1 } { 2 } \ ) thì tại M là cực tiểu giao thoa thứ ( k + 1 )+ Khoảng cách giữa hai đỉnh liên tục của hai hypecbol cùng loại ( giữa hai cực lớn ( hai cực tiểu ) giao thoa ) : λ / 2 .
+ Số đường dao động với Amax và Amin :
v Số đường giao động với Amax ( luôn là số lẻ ) là số giá trị của k thỏa mãn nhu cầu điều kiện kèm theo( không tính hai nguồn ) :
* Số Cực đại: \(-\frac{1}{\lambda }< k< \frac{1}{\lambda }\) và \(k\in Z\)
Vị trí của những điểm cực lớn giao thoa xác lập bởi : \ ( d_ { 1 } = k. \ frac { \ lambda } { 2 } + \ frac { AB } { 2 } \ ) ( thay những giá trị tìm được của k vào )v Số đường giao động với Amin ( luôn là số chẵn ) là số giá trị của k thỏa mãn nhu cầu điều kiện kèm theo( không tính hai nguồn ) :
* Số Cực tiểu: \(-\frac{1}{\lambda } -\frac{1}{2}< k< \frac{1}{\lambda }-\frac{1}{2}\) và \(k\in Z\)
Hay \ ( – \ frac { 1 } { \ lambda } < k + 0,5 < \ frac { 1 } { \ lambda } \ )Vị trí của những điểm cực tiểu giao thoa xác lập bởi : \ ( d_ { 1 } = k. \ frac { \ lambda } { 2 } + \ frac { AB } { 2 } + \ frac { \ lambda } { 4 } \ ) ( thay những giá trị của k vào ) .=> Số cực lớn giao thoa bằng số cực tiểu giao thoa + 1 .

c. Số điểm (đường) dao động cực đại, cực tiểu giữa hai điểm M, N thỏa mãn :
\ ( \ Delta d_ { M } \ leq ( d_ { 1 } – d_ { 2 } ) = ( \ Delta \ varphi _ { M } – \ Delta \ varphi ) \ frac { \ lambda } { 2 \ pi } \ leq \ Delta d_ { N } \ ) ( 3 )( Hai điểm M, N cách hai nguồn lần lượt là d1M, d2M, d1N, d2N. )
Ta đặt ∆dM= d1M – d2M ; ∆dN = d1N – d2N, giả sử: ∆dM < ∆dN
Với số giá trị nguyên của k thỏa mãn biểu thức trên là số điểm (đường) cần tìm giữa hai điểm M và N.
Chú ý: Trong công thức (3) Nếu M hoặc N trùng với nguồn thì không dủng dấu BẰNG
( chỉ dùng dấu < ) Vì nguồn là điểm đặc biệt quan trọng không phải là điểm cực lớn hoặc cực tiểu !
d.Tìm số đường dao động cực đại và không dao động giữa hai điểm M, N bất kỳ
Hai điểm M, N cách hai nguồn lần lượt là d1M, d2M, d1N, d2N .
Đặt ∆ dM = d1M – d2M ; ∆ dN = d1N – d2N và giả sử ∆ dM < ∆ dN .+ Hai nguồn xê dịch cùng pha :
* Cực đại: ∆dM < kλ < ∆dN
* Cực tiểu: ∆dM < (k+0,5)λ < ∆dN
+ Hai nguồn giao động ngược pha :
* Cực đại: ∆dM < (k+0,5)λ < ∆dN
* Cực tiểu: ∆dM < kλ < ∆dN
Số giá trị nguyên của k thoả mãn những biểu thức trên là số đường cần tìm .
B. CÁC DẠNG BÀI TẬP
Bài toán 1. Bài toán xác định số cực đại – cực tiểu
Cực đại cực tiểu trên đoạn S1S2 ( trên đường nối hai nguồn )Max : \ ( – \ frac { 1 } { \ lambda } \ leq k \ leq \ frac { 1 } { \ lambda } \ ) Min : \ ( – \ frac { 1 } { \ lambda } – \ frac { 1 } { 2 } \ leq k \ leq \ frac { 1 } { \ lambda } – \ frac { 1 } { 2 } \ )\ ( N_ { max } = 2 \ left [ \ frac { l } { \ lambda } \ right ] + 1 \ ) \ ( N_ { min } = 2 \ left [ \ frac { l } { \ lambda } + \ frac { 1 } { 2 } \ right ] \ )
Ví dụ 1: Trong thí nghiệm giao thoa sóng trên mặt nước hai nguồn kết hợp A, B cách nhau 12,5cm dao động cùng pha với tần số 10Hz. Tốc độ truyền sóng trên mặt nước là 20cm/s. Tính số đường dao động cực đại, cực tiểu trên mặt nước là:
Hướng dẫn: Cực đại: \(-\frac{1}{\lambda }\leq k\leq \frac{1}{\lambda }\) Trong đó: l = 12,5 cm và \(\lambda =\frac{v}{f}=\frac{20}{10}\) = 2 cm
Thay vào : => \ ( – \ frac { 12,5 } { 2 } \ leq k \ leq \ frac { 12,5 } { 2 } \ Leftrightarrow – 6,25 \ leq k \ leq 6,25 \ Rightarrow \ ) Có 13 giá trị của k nên có 13 đườngCực tiểu làm tương tự như ….
Bài toán 2. Bài toán đường trung trực
Cho 2 nguồn sóng S1 ; S2 giống nhau cùng giao động điều hòa với phương trình : u1 = u2 = U0cos ( ωt ). Gọi I là dao điểm của đường trung trực và hai nguồn S1 ; S2. Trên đường trung trực ta chọn lấy điểm M sao cho M xê dịch cùng pha với hai nguồn và gần I nhất .a. Hãy viết phương trình giao động tại Mb. Xác định IMc. Gọi C là điểm bất kể nằm trên đường trung trực của hai nguồn. Xác định trên đoạn CI có bao nhiêu điểm giao động cùng pha với hai nguồn .d. Gọi N là điểm bất kể nằm trên đường trung trực của hai nguồn. Xác định trên đoạn NI có bao nhiêu điểm xê dịch ngược pha với hai nguồn .

Bài toán 3. Bài toán xác định biên độ giao thoa sóng khi độ lệch pha khác 0
Tại vị trí M bất kể. AM = | 2U0 cos [ \ ( – \ frac { \ Delta \ varphi } { 2 } + \ frac { \ pi ( d_ { 2 } – d_ { 1 } ) } { \ lambda } \ ) ] |Tại trung điểm của S1S2 : AM = | 2. Uo cos ( \ ( – \ frac { \ Delta \ varphi } { 2 } \ ) ) |Hai nguồn cùng pha : AM = 2U0Hai nguồn ngược pha : AM = 0Hai nguồn vuông pha : AM = U0 \ ( \ sqrt { 2 } \ )Hai nguồn lệch sóng \ ( \ frac { \ pi } { 3 } \ ) : AM = U0 \ ( \ sqrt { 3 } \ )
Ví dụ 3: Thực hiện thí nghiệm giao thoa sóng cơ trên mặt nước với hai nguồn cùng pha có tần số 10 Hz, vận tốc truyền sóng trên mặt nước là v = 50 cm/s. Hỏi tại vị trí M cách nguồn 1 một đoạn d1 = 17,5 cm và cách nguồn 2 một đoạn d2 = 25 cm, là điểm cực đại hay cực tiểu, cực đại hay cực tiểu số mấy?
Hướng dẫn: Ta có: d2 – d1 = 25 – 17,5 = 7,5cm và \(\lambda =\frac{v}{f}=\frac{50}{10}\)= 5 cm. Vì ∆d = 1,5.λ => k = 1
=> Nằm trên đường cực tiểu số 2 .
Ví dụ 4: Thực hiện thí nghiệm giao thoa sóng cơ trên mặt nước với hai nguồn cùng pha có tần số là 10 Hz. M là một điểm cực đại có khoảng cách đến nguồn 1 là d1 = 25 cm và cách nguồn 2 là d2 = 35 cm. Biết giữa M và đường trung trực còn có 1 cực đại nữa. Xác định vận tốc truyền sóng trên mặt nước?
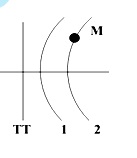
Vì giữa M và đường trung trực còn 1 đường cực lớn nữa, nên M nằm trên đường cực lớn thứ 2 Þ k = 2. Ta có : ∆ dM = d2 – d1 = 35 – 25 = 2. λ=> λ = 5 cm => v = λ. f = 5.10 = 50 cm

C. MỘT SỐ CÂU HỎI TRONG ĐỀ THI ĐẠI HỌC
Câu 1 (ĐH 2013): Trong một thí nghiệm về giao thoa sóng nước, hai nguồn sóng kết hợp dao động cùng pha đặt tại hai điểm A và B cách nhau 16cm. Sóng truyền trên mặt nước với bước sóng 3cm. Trên đoạn AB, số điểm mà tại đó phần tử nước dao động với biên độ cực đại là:
A. 9 B. 10 C. 11 D. 12.
Câu 2 (ĐH 2014): Trong một thí nghiệm giao thoa sóng nước, hai nguồn S1 và S2 cách nhau 16cm, dao động theo phương vuông góc với mặt nước, cùng biên độ, cùng pha, cùng tần số 80Hz. Tốc độ truyền sóng trên mặt nước là 40cm/s. Ở mặt nước, gọi d là đường trung trực của đoạn S1S2. Trên d, điểm M ở cách S1 10cm; điểm N dao động cùng pha với M và gần M nhất sẽ cách M một đoạn có giá trị gần giá trị nào nhất sau đây?
A. 7,8mm B. 6,8mm C. 9,8mm D. 8.8mm
Tất cả nội dung bài viết. Các em hãy xem thêm và tải file chi tiết dưới đây:
Luyện Bài tập trắc nghiệm môn Vật lý lớp 12 – Xem ngay
Source: http://wp.ftn61.com
Category: Hỏi Đáp


Để lại một bình luận