I. Sơ đồ tư duy toán 9 chương 1 hình học
1. Sơ đồ tư duy toán 9 chương 1 hình học – hệ thức lượng trong tam giác vuông
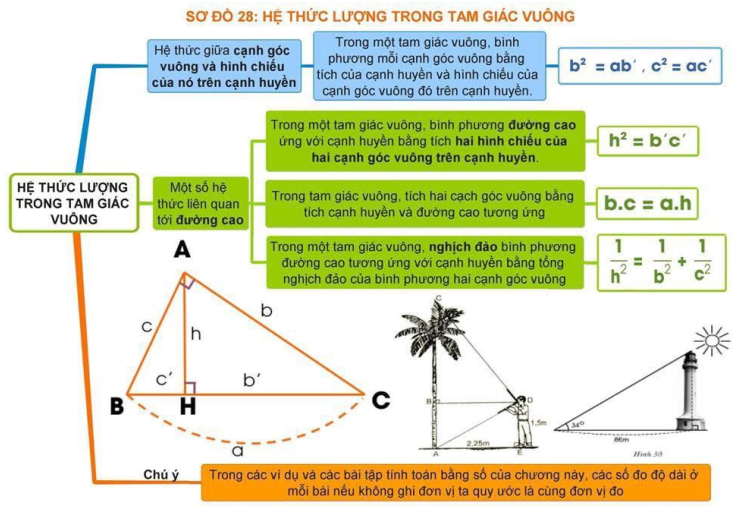
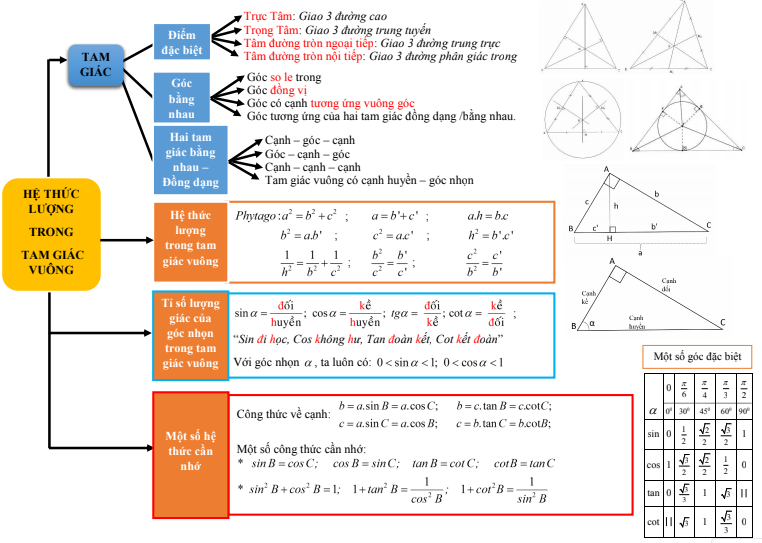
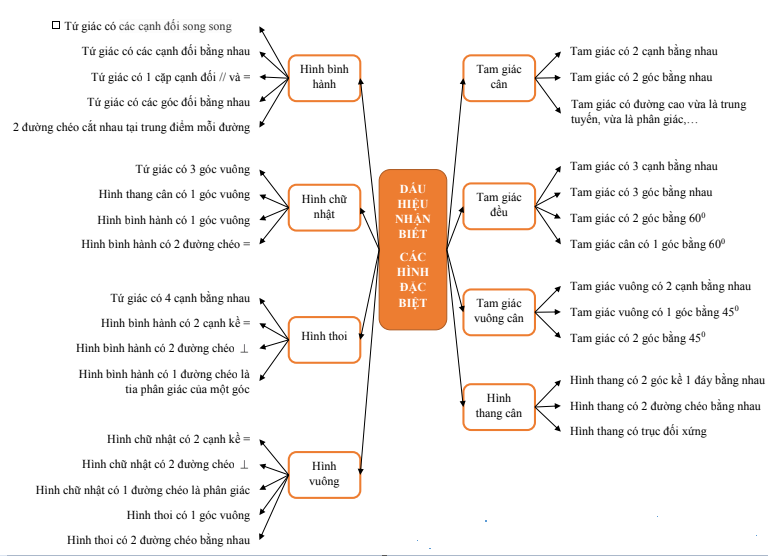
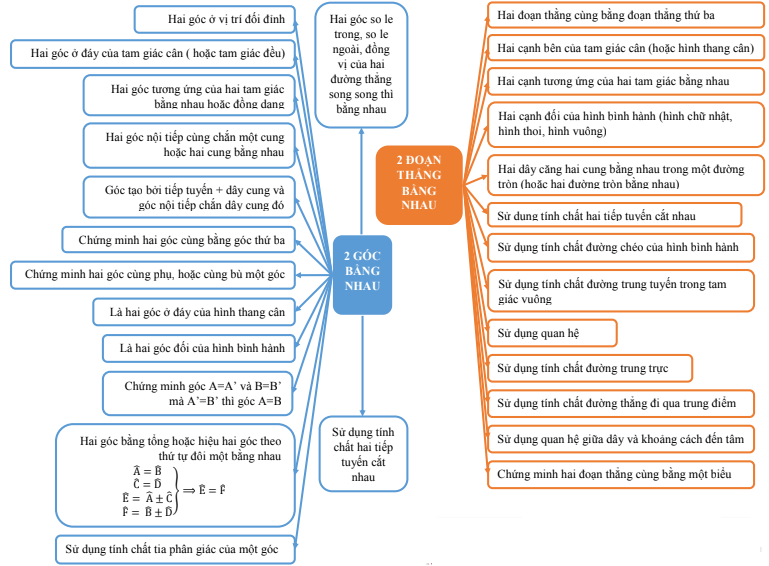
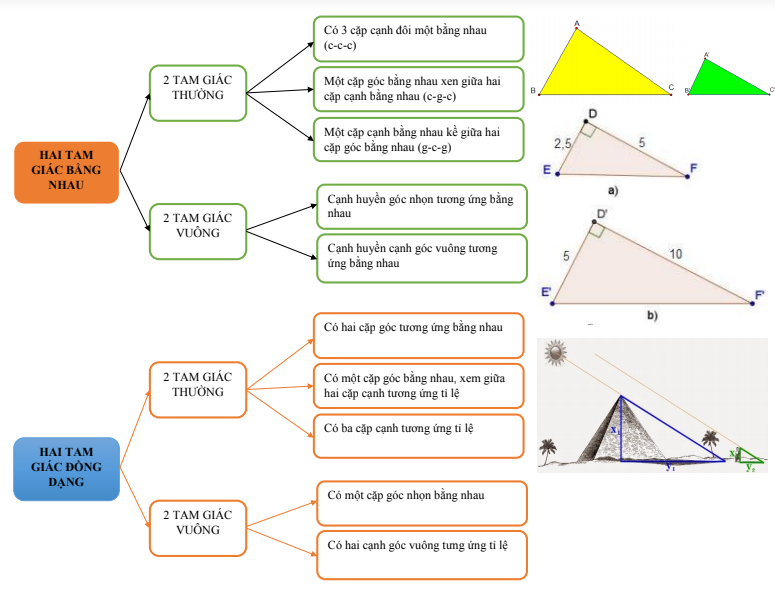
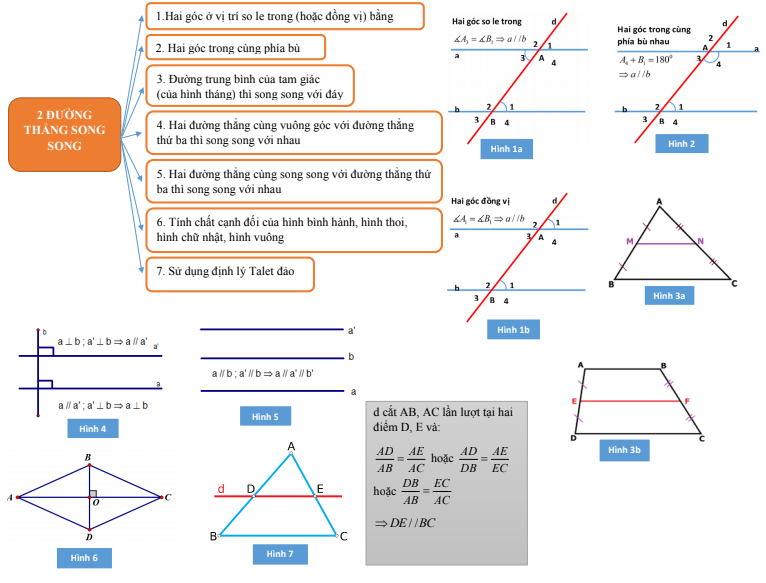
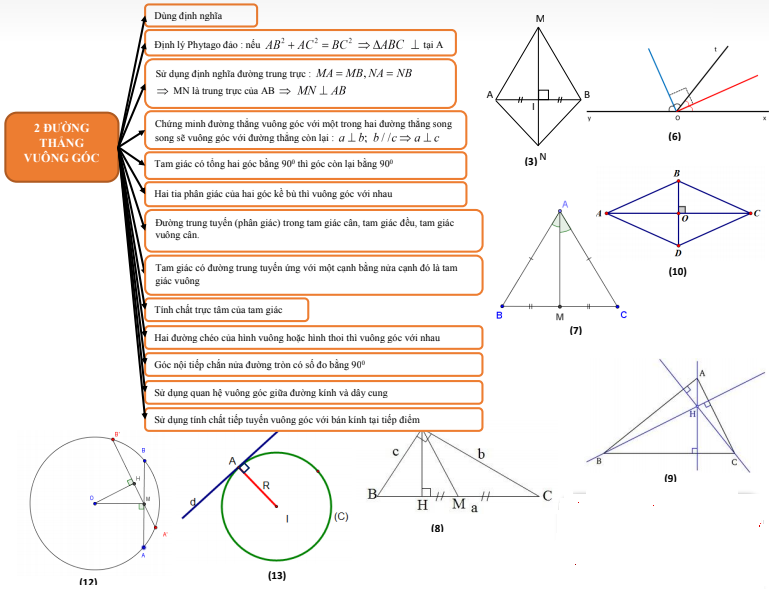
2. Sơ đồ tư duy toán 9 chương 1 hình học – bổ trợ kiến thức hình học THCS
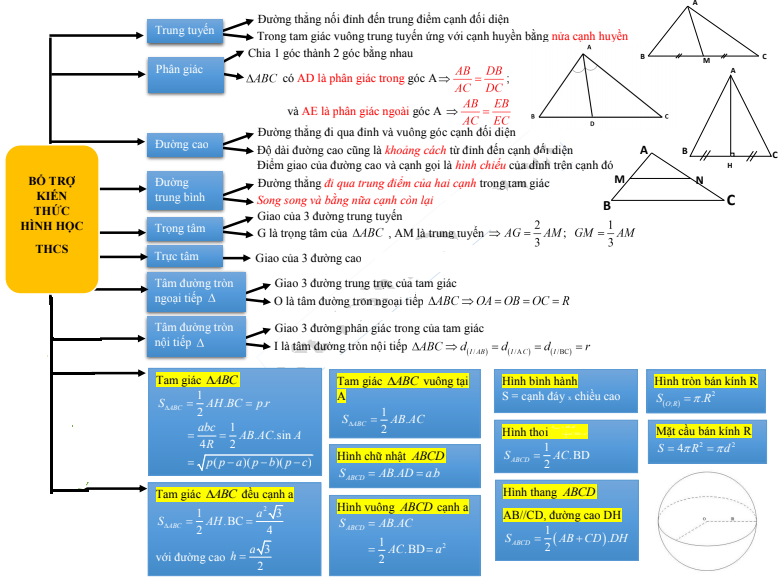
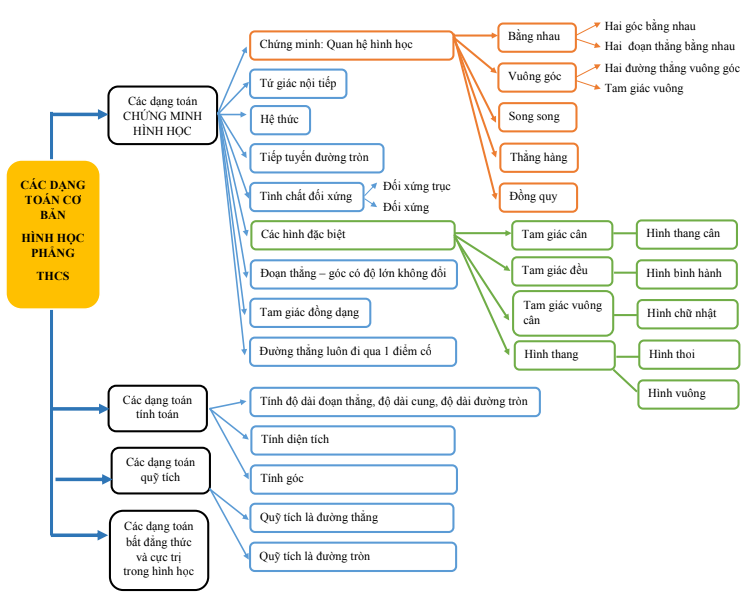
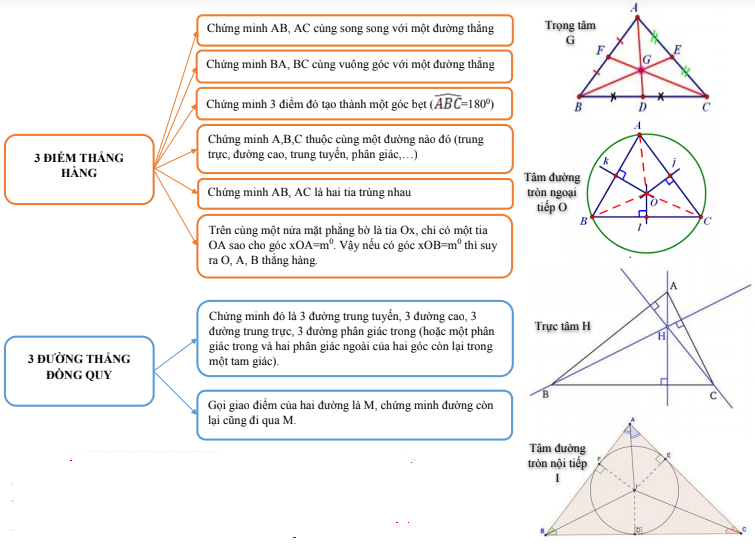
II. Tổng hợp lý thuyết Chương 1 Hình học 9 ngắn gọn, hay nhất
1. Hệ thức về cạnh và đường cao
Tam giác ABC vuông tại A, đường cao AH, ta có :
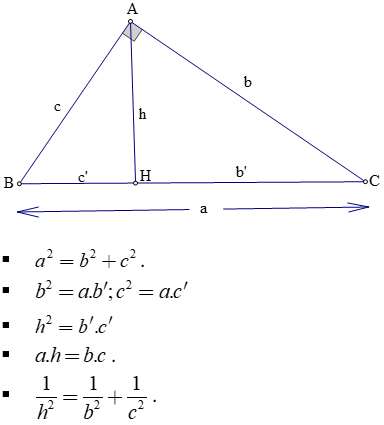
Chú ý : Diện tích tam giác vuông : S = ( 50% ) bc = ( 50% ) ah .
2. Tỉ số lượng giác của góc nhọn.
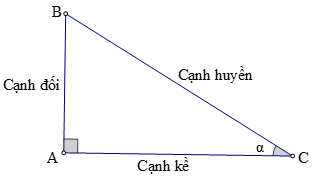
+ Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin của góc α, kí hiệu là sinα .
+ Tỉ số giữa cạnh kề và cạnh huyền được gọi là côsin của góc α, kí hiệu là cosα .
+ Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của góc α, kí hiệu là tanα .
+ Tỉ số giữa cạnh kề và cạnh đối được gọi là côtang của góc α, kí hiệu là cotα .
Hay sinα = AB / BC ; cosα = AC / BC ; tanα = AB / AC ; cotα = AC / AB .
Tính chất:
+ Nếu α là một góc nhọn thì 0 < sinα < 1 ; 0 < cosα < 1 ; tanα > 0 ; cotα > 0 .
Ta có: sin2α + cos2α = 1;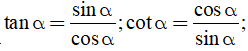 
tanα.cotα = 1
+ Với hai góc nhọn α, β mà α + β = 90 ° .
Ta có : sinα = cosβ ; cosα = sinβ ; tanα = cotβ ; cotα = tanβ .
Nếu hai góc nhọn α và β có sinα = sinβ hoặc cosα = cosβ thì α = β .
3. Hệ thức về cạnh và góc trong tam giác vuông.
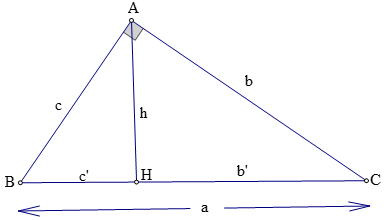
Trong một tam giác vuông, mỗi cạnh góc vuông bằng :
+ Cạnh huyền nhân với sin góc đối hay nhân với côsin góc kề .
+ Cạnh góc vuông kia nhân với tan của góc đối hay nhân với cotg của góc kề .
b = a. sinB = a. cosC ; c = a. sinC = a. cosB ; b = c. tgB = c. cotgC ; c = b. tgC = b. cotgC .
Chú ý: Trong một tam giác vuông nếu cho trước hai yếu tố (trong đó có ít nhất một yếu tố về cạnh và không kể góc vuông) thì ta sẽ tìm được các yếu tố còn lại.
III. Một số dạng bài tập toán 9 chương 1 hình học
Câu 1: Cho tam giác cân ABC có đáy BC = 2a, cạnh bên bằng b (b > a) .
a ) Tính diện tích quy hoạnh tam giác ABC
b) Dựng BKk ⊥ AC. Tính tỷ số 
.
Lời giải
a ) Gọi H là trung điểm của BC. Theo định lý Pitago ta có :
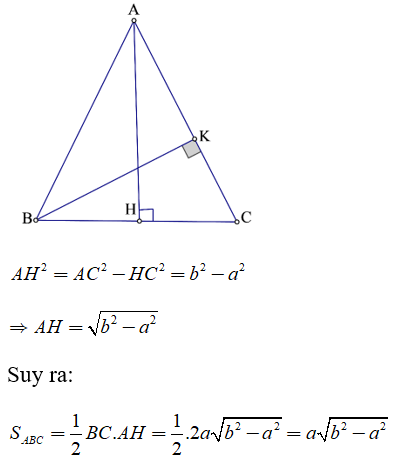
b ) Ta có
Câu 2: Cho tam giác ABC với các đỉnh A, B, C và các cạnh đối diện với các đỉnh tương ứng là: a, b, c .
a ) Tính diện tích quy hoạnh tam giác ABC theo a, b, c
b ) Chứng minh : a2 + b2 + c2 ≥ 4 √ 3S
Lời giải
Xem thêm: Bộ Kế hoạch Đầu tư Tiếng Anh là gì?
a ) Ta giả sử góc A là góc lớn nhất của tam giác
ABC ⇒ B, C là những góc nhọn .
Suy ra chân đường cao hạ từ A lên BC là điểm H thuộc cạnh BC .
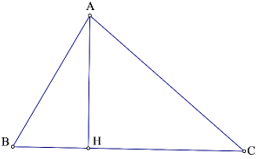
Ta có : BC = Bảo hành + HC .
Áp dụng định lý Py ta go cho những tam giác vuông AHB, AHC ta có :
AB2 = AH2 + HB2 ; AC2 = AH2 + HC2
Trừ hai đẳng thức trên ta có :
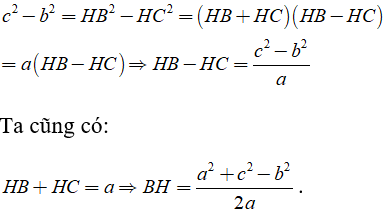
Áp dụng định lý Pitago cho tam giác vuông AHB
b ) Từ câu a ) ta có :
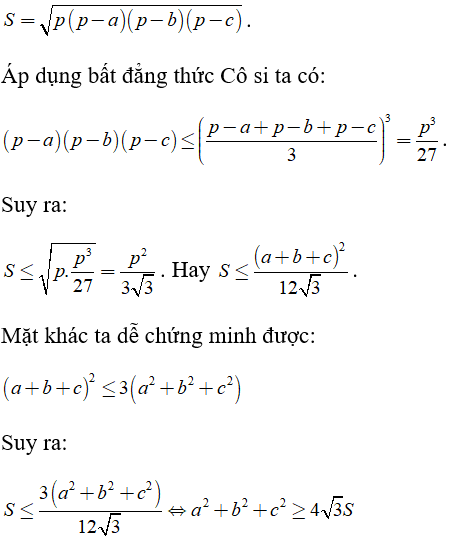
Dấu bằng xảy ra khi và chỉ khi tam giác ABC đều .
Câu 3: Biết sinα 5/13. Tính cosα, tanα và cotα .
Lời giải
Xét Δ vuông tại A .
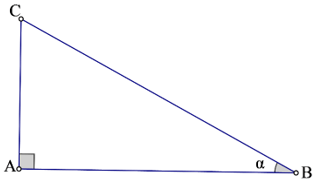
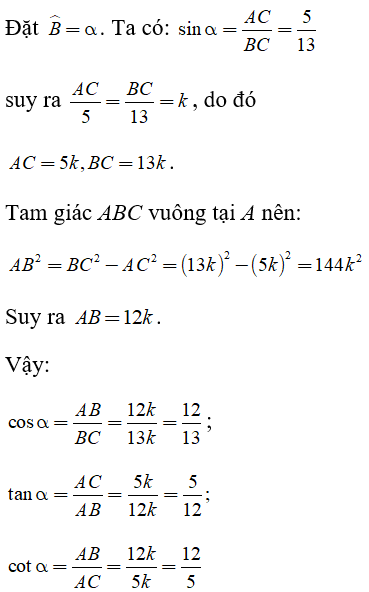
Câu 4: Biết sinα.cosα = 12/25. Tính sinα.cosα.
Lời giải
Biết sinα. cosα = 12/25. Để tính sinα. cosα ta cần tính sinα + cosα rồi giải phương trình với ẩn là sinα hoặc cosα .
Ta có :
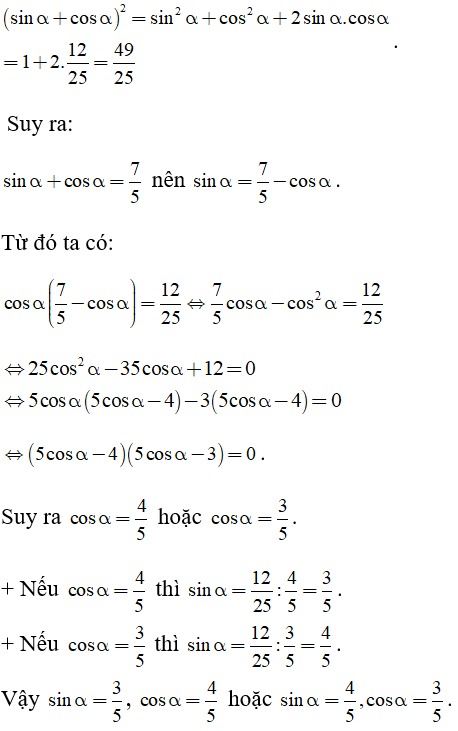
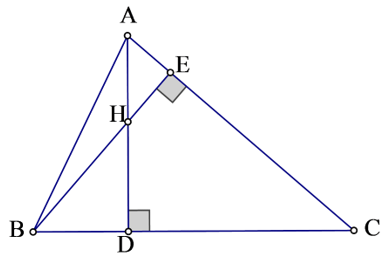
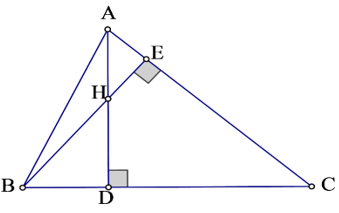
Câu 5: Cho tam giác nhọn ABC hai đường cao AD và BE cắt nhau tại H. Biết HD:HA = 1:2. Chứng minh rằng tgB.tgC = 3 .
Lời giải
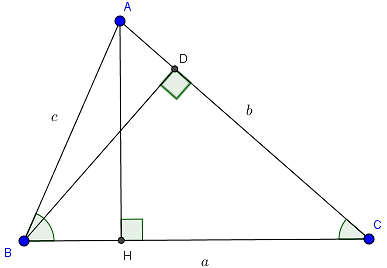
Câu 6: Cho tam giác ABC nhọn. Gọi a, b, c lần lượt là độ dài các cạnh đối diện với các đỉnh A, B, C. Chứng minh rằng: 
Lời giải
Câu 7: Ở một cái thang đơn dài có ghi “để dảm bảo an toàn cần đặt thang sao cho tạo với mặt đất một góc α thì phải thỏa mãn 60° < α < 75°. Vậy phải đặt thang cách vật thang dựa khoảng bao nhiêu để đảm bảo an toàn?
Lời giải
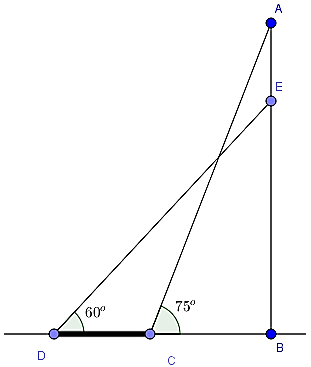
Ta xem đề bài như hình vẽ trên
Khi đó : Khoảng bảo đảm an toàn nằm trong khoảng chừng từ C đến D
Ta có :
BC = AC.cos 75 ° = 3. cos75 ° ≃ 0,776 ( m )
BD = ED.cos 60 ° = 1,5 ( m )
Vậy phải đặt thang cách vật dựa một đoạn l ( m ) thỏa mãn nhu cầu 0,776 ( m ) < l < 1,5 ( m )
Câu 8: Cho tam giác ABC vuông tại B có BC = 20m, 
. Một đường thẳng song song với BC cắt AB, AC lần lượt tại D, E. Biết BD = 5m. Tính độ dài AE là?
Lời giải
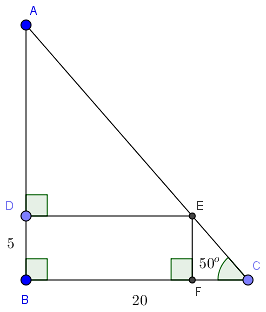
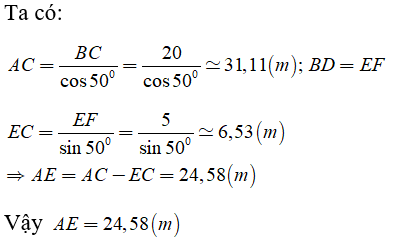
Vậy là các em đã hoàn thành chuyên đề Sơ đồ tư duy Toán 9 chương 1 hình học, Top lời giải hi vọng các em đã nắm chắc lý thuyết và vận dụng vào các bài tập liên quan đến hệ thức lương trong tam giác vuông. Cùng theo dõi Top lời giải và xem thêm các chuyên đề hay ở trong chuyên mục này nhé. Hãy đặt câu hỏi giúp phần comment để đội ngũ thầy cô giáo của Top lời giải hỗ trợ tốt hơn cho bạn.
Source: http://wp.ftn61.com
Category: Hỏi Đáp
Để lại một bình luận